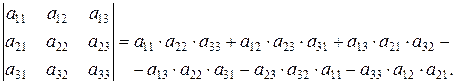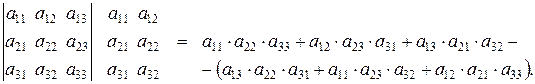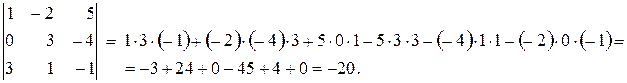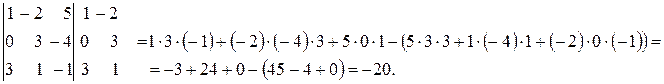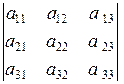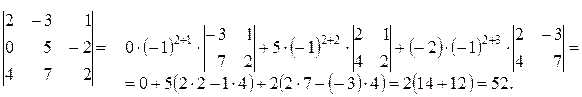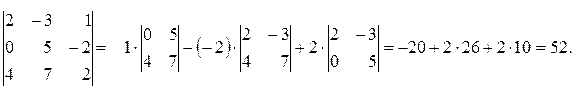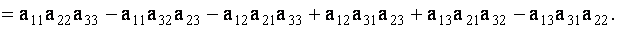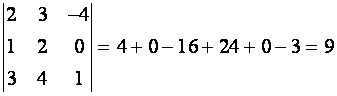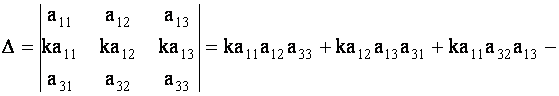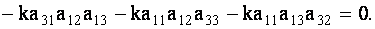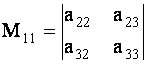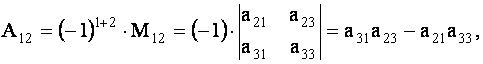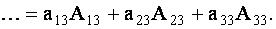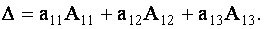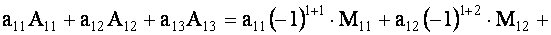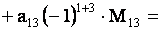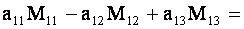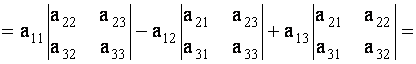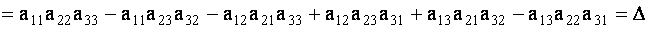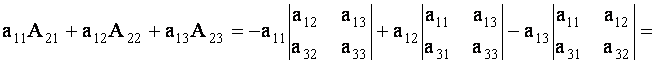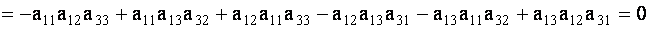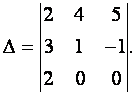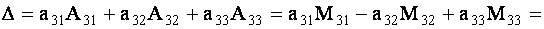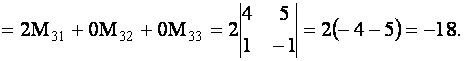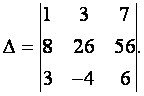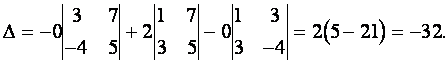- Методы вычисления определителя третьего порядка
- Методы вычисления определителей
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Приведение определителя к треугольному виду
- Теорема Лапласа
- Математика — онлайн помощь
Методы вычисления определителя третьего порядка
Определители и способы их вычисления
Определитель – это число, соответствующее квадратной матрице, вычисленное определенным образом.
Определителем второго порядка называется число, определяемое равенством:
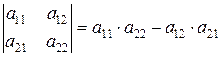
Пример 3.1.
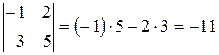
Определителем третьего порядка называется число, определяемое квадратной матрицей третьего порядка.
1.Метод треугольников (метод Саррюса)
То есть, если элементы определителя третьего порядка записать в таблицу 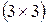
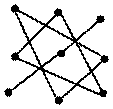 |
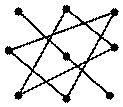 |
| Рис. 1 |
Это правило называется правилом Саррюса.
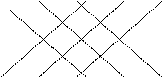
2. Метод дописывания двух столбцов.
Этот способ вычисления определителя третьего порядка заключается в дописывании первых двух столбцов определителя и нахождении суммы произведений по главной диагонали и параллелях к ней за вычетом суммы произведений побочной диагонали и параллелях к ней, т.е.
Пример 3.2. Вычислить определитель двумя способами
3. Третий способ вычисления определителя основан на теореме разложения.
Минором элемента определителя 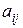
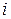
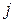
Например, минором элемента 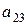
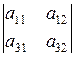
т.е. из исходного определителя были вычеркнуты вторая строка и третий столбец.
Алгебраическим дополнением 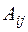
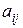
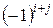
При этом полезно иметь в виду следующую схему:
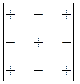 | где знаком плюс отмечены места тех элементов, для которых алгебраические дополнения равны минорам, взятым с их собственным знаком; и знаком минус те, для которых алгебраические дополнения равны минорам, взятым с противоположным знаком. |
| Теорема разложения | Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения. |
Пример 3.3. Вычислить определитель путем разложения: а) по второй строке; б) по третьему столбцу.
а)
б)
Замечание. Если в задании не указано, по какому столбцу (строке) проводить разложение, то лучше выбирать столбец (строку) с большим числом нулей.
Определитель 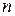
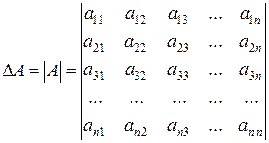
Вычисление определителей порядка больше 3, рекомендуется проводить с помощью теоремы разложения.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Методы вычисления определителей
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
Задание. Вычислить определитель второго порядка $\left| \begin
Решение. $\left| \begin
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Вычислить определитель $\left| \begin
Решение. $\left| \begin
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
Задание. Вычислить определитель $\left| \begin
Решение.
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель $\left| \begin
Решение. $\left| \begin
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Задание. Вычислить определитель $\left| \begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Задание. Вычислить определитель $\left| \begin
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Задание. Вычислить определитель $\Delta=\left| \begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $\Delta=-80$
Теорема Лапласа
Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin
Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Источник
Математика — онлайн помощь
Пусть дана квадратная матрица третьего порядка
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
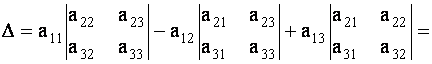 | (1.7) |
Определитель третьего порядка обозначается символом
 | (1.8) |
где числа 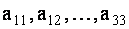
Индексы 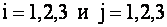
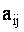
Например, элемент 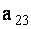
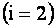
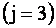
Элементы 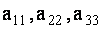
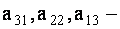
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором 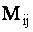
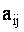
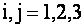
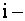
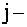
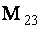
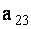
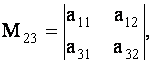
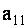
С помощью миноров определитель (7) можно записать в виде
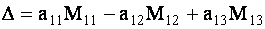 | (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением 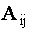
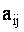
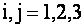
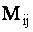
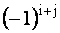
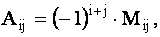 где где 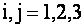 / / | (1.10) |
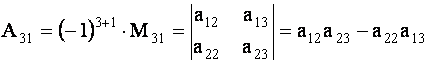
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
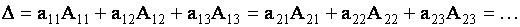 | (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы 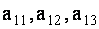
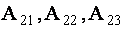
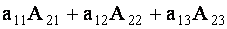
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим 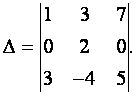
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник