Способы нахождения двугранного угла

Двугранные углы. Углы между плоскостями.
Перпендикулярность плоскостей

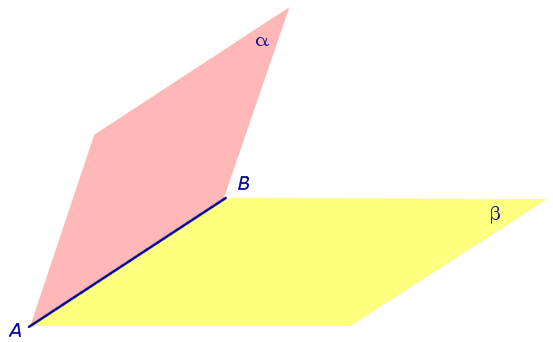
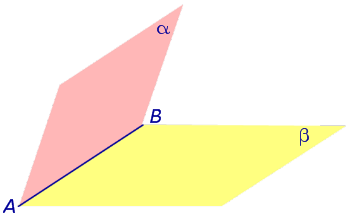
Двугранным углом называют часть пространства, ограниченную двумя полуплоскостями с общей границей (рис. 1)

Полуплоскости α и β , ограничивающие двугранный угол, называют гранями двугранного угла , а их общую границу AB называют ребром двугранного угла .

Двугранные углы называют равными двугранными углами , если их можно совместить.

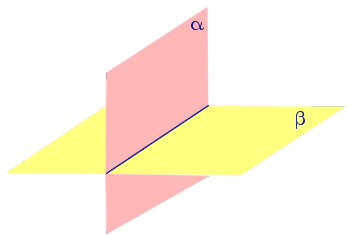
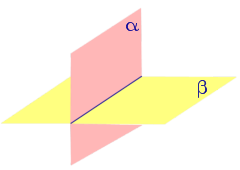
При пересечении двух плоскостей образуются четыре двугранных угла (рис. 2). Наименьший из этих углов обычно и называют углом между плоскостями .

Если при пересечении двух плоскостей образовалось 4 равных двугранных угла, то такие двугранные углы называют прямыми двугранными углами , а сами плоскости называют перпендикулярными плоскостями (рис. 3).

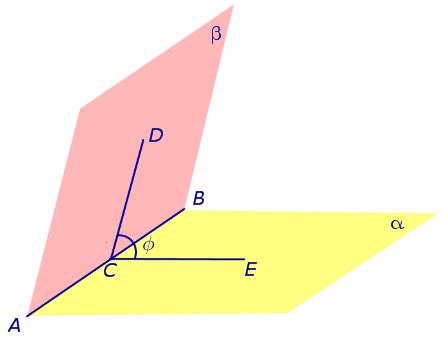
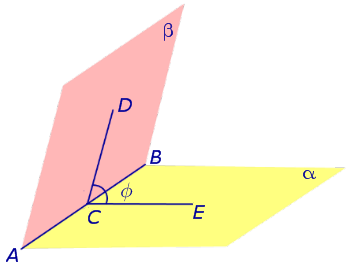
Выберем произвольную точку С на ребре AB двугранного угла и проведем через нее перпендикуляры CD и CE в каждой из граней двугранного угла. Угол DCE , образованный перепендикулярами CD и CE, называют линейным углом двугранного угла (рис. 4).

На рисунке 4 угол φ является линейным углом двугранного угла с гранями α и β и ребром AB .

Линейные углы двугранных углов используются, в частности, для того, чтобы измерять двугранные углы. Например, если линейный угол двугранного угла равен 30° ( или 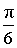) , то и двугранный угол равен 30° ( радиан ) . Соответственно, прямой двугранный угол равен 90° ( радиан ) .

Источник

Лекция по математике на тему «Двугранный угол»

Лекция по теме «Двугранный угол»

В планиметрии основными объектами являются прямые, отрезки, лучи и точки. Лучи исходящие из одной точки, образуют одну их геометрических фигур–угол.

Мы знаем, что линейный угол измеряется в градусах и радианах.

В стереометрии к объектам добавляется плоскость. Фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не принадлежащими одной плоскости в геометрии называется двугранным углом. Полуплоскости – это грани двугранного угла. Прямая а – это ребро двугранного угла.

Двухгранный угол как и линейный угол можно назвать, измерить, построить. Это и предстоит нам выяснить в этом уроке.

Найдём двухгранный угол на модели тетраэдра АВС D .

Двугранный угол с ребром АВ называют CABD , где С и D точки принадлежащие разным граням угла а ребро АВ называют в середине

Вокруг нас достаточно много предметов с элементами в виде двухгранного угла.

Во многих городах в парках установлены специальные скамейки для примирения. Скамейка выполнена в виде двух сходящихся к центру наклонных плоскостей.

При строительстве домов часто используется так называемая двухскатная крыша. На этом доме крыша выполнена в виде двухгранного угла в 90 градусов.

Двугранный угол тоже измеряется в градусах или радианах, но как его измерить.

Интересно заметить, что крыши домов лежат на стропилах. А обрешётка стропил образует два ската крыши под заданным углом.

Перенесем изображение на чертёж. На чертеже для нахождения двухгранного угла на его ребре отмечается точка В. Из этой точки проводятся два луча ВА и ВС перпендикулярно ребру угла. Образованный этими лучами угол АВС называется линейным углом двугранного угла.

Градусная мера двугранного угла равна градусной мере его линейного угла.

Измерим угол АОВ.

Градусная мера данного двугранного угла равна шестидесяти градусам.

Линейных углов для двугранного угла можно провести бесконечное количество, важно знать, что все они равны.

Рассмотрим два линейных угла АОВ и А ₁ О ₁ В ₁ . Лучи ОА и О ₁ А ₁ лежат в одной грани и перпендикулярны к прямой ОО ₁ , поэтому они сонаправлены. Лучи ОВ и О ₁ В ₁ так же сонаправлены. Поэтому угол АОВ равен углуА ₁ О ₁ В ₁ как углы с сонаправленными сторонами.

Так двугранный угол характеризуется линейным углом, а линейные углы бывают острые, тупые и прямые. Рассмотрим модели двугранных углов.

Тупой угол, если его линейный угол от 90 до 180 градусов.

Прямой угол, если его линейный угол равен 90 градусов.

Острый угол, елси его линейный угол от 0 до 90 градусов.

На экране изображение

На экране изображение и текст

прямая а –ребро угла

Фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не принадлежащие одной плоскости.

На экране изображение

На экране обновляется изображение и текст

CABD – двухгранный угол.

Обозначение C AB D ,

АВ– ребро, САВС, DACD

На экране изображение

На экране изображение На экране изображение

На экране изображение

АВС– линейный угол, АВа, ВСа

Градусной мерой двугранного угла называется градусная мера его линейного угла.

На экране появляется анимацию по измерению градусной меры линейного угла с наложением транспортира):

На экране изображение с анимацией элементов.

ОА и О ₁ А ₁ , ОВ и О ₁ В ₁ – сонаправлены

На экране изображение с анимацией появления.

Докажем одно из важных свойств линейного угла.

Плоскость линейного угла перпендикулярна к ребру двугранного угла.

Пусть угол АОВ – линейный угол данного двугранного угла. По построению лучи АО и ОВ перпендикулярные прямой а.

Через две пересекающиеся прямые АО и ОВ проходит плоскость АОВ по теореме: Через две пересекающиеся прямые проходит плоскость и притом только одна.

Прямая а перпендикулярна двум пересекающимся прямым лежащим в этой плоскости, значит по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости АОВ.

Плоскость линейного угла перпендикулярна к ребру двугранного угла.

На экране изображение и доказательство:

АО, ОВ а (по построению)

На экране добавляется пункт доказательства:

АО АОВ единственная

На экране добавляется пункт доказательства и чертёж

Для решения задач важно уметь строить линейный угол заданного двухгранного угла. Построить линейный угол двугранного угла с ребром АВ для тетраэдра АВС D .

Речь идет о двугранном угле, который образован, во-первых, ребром АВ, одной гранью АВ D , второй гранью АВС.

Вот один из способов построения.

Проведем перпендикуляр из точки D к плоскости АВС, Отметим точку М основание перпендикуляра. Вспомним, что в тетраэдре основание перпендикуляра совпадает с центром вписанной окружности в основание тетраэдра.

Проведем наклонную из точки D перпендикулярно к ребру АВ, отметим точку N основание наклонной.

В треугольнике DMN отрезок NM будет проекций наклонной DN на плоскость АВС. По теореме о трёх перпендикулярах ребро АВ будет перпендикулярно проекции N М.

Значит c тороны угла DNM перпендикулярны к ребру АВ, значит построенный угол DNM искомый линейный угол.

На экране изображение с анимацией элементов:

На экране изображение и текст:

На экране обновляется чертёж и текст:

На экране обновляется чертёж и построения:

DM ⊥ NM , АВ ⊥ DN АВ ⊥ NM

На экране добавляется пункт построения:

Рассмотрим пример решения задачи на вычисление двугранного угла.

Равнобедренный треугольник АВС и правильный треугольник А DB не лежат в одной плоскости. Отрезок CD является перпендикуляром к плоскости ADB . Найдите двугранный угол DABC , если AC = CB =2 см, А B = 4см.

Двугранный угол DABC равен его линейному углу. Построим этот угол.

Проведем наклонную СМ перпендикулярно к ребру АВ, так как треугольник АСВ равнобедренный, то точка М совпадёт с серединой ребра АВ.

Прямая С D по условию перпендикулярна плоскости ADB , значит перпендикулярна прямой DM лежащей в этой плоскости. А отрезок М D является проекцией наклонной СМ на плоскость А D В.

Прямая АВ перпендикулярна наклонной СМ по построению, значит по теореме о трех перпендикулярах перпендикулярна проекции MD .

Итак к ребру АВ найдены два перпендикуляра СМ и D М. Значит они образуют линейный угол С MD двугранного угла D АВС. И нам останется его найти из прямоугольного треугольника С DM .

Так отрезок СМ медиана и высота равнобедренного треугольника АСВ, то по теореме Пифагора катет СМ равен 4 см.

Из прямоугольного треугольника DMB по теореме Пифагора катет DM равен двум корням из трёх.

Косинус угла из прямоугольного треугольника равен отношению прилежащего катета М D к гипотенузе СМ и равен три корня из трёх на два. Значит угол СМ D равен 30 градусам.

На экране текст задачи и изображение:

ΔА DB правильный не лежат в

одной плоскости, CD ADB .

AC = CB =2 см, А B = 4см

Найти: угол DABC ,

1) Проведём СМ: СМАВ, АМ=МВ (по свойству р/б треу-ка)

На экране изображение и текст решения:

2) CD ( ADB ) MD , и М D -проекция СМ

На экране добавляется пункт решения и отметки прямых углов:

3) АВ СМ, где СМ –наклонная, а М D -проекция

На экране обновляется чертёж и текст решения:

искомый линейный угол.

На экране обновляется чертёж и текст решения:

На экране добавляется пунк решения:

Δ D МВ– прям. D М= см.

На экране добавляется пунк решения:

ΔС D М– прям cos ==30°

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 807 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 284 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 603 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-025649

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В российских школах оборудуют кабинеты для сообщества «Большой перемены»

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

В проекте КоАП отказались от штрафов для школ

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник