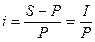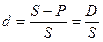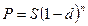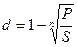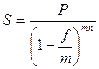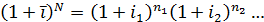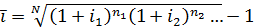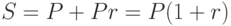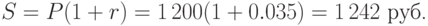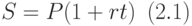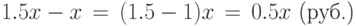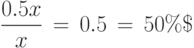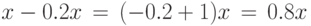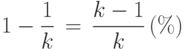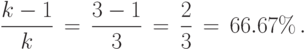Лекция № 1 . Способы начисления процентов и виды
Лекция № 1 . Способы начисления процентов и виды
Процентных ставок.
Вопросы.
Основные понятия.
Способы начисления процентов и виды процентных ставок.
Начисление простых процентов.
Начисление простых процентов по ссудным ставкам.
Начисление простых процентов по учетным ставкам.
Начисление сложных процентов.
Начисление сложных процентов по ссудным ставкам.
Начисление сложных процентов по учетным ставкам.
Непрерывное начисление процентов.
Эквивалентные и эффективные процентные ставки.
Уравнивающие ставки.
Средние ставки.
Вопрос 1. Основные понятия.
Проценты (процентные деньги) ( I ) – это абсолютная величина дохода от инвестиций производственного или финансового характера, а также абсолютное выражение расходов по оплате за пользование ресурсами.
Процентная ставка (норма процента) – относительная величина, характеризующая интенсивность начисления процентов и показывающая, на сколько процентов изменится стоимость за определенный интервал времени. Она является одним из важнейших элементов коммерческих, кредитных и инвестиционных контрактов и измеряется в виде десятичной дроби, обыкновенной дроби или в процентах.
Период начисления (конверсионной период, срок операции) ( n ) – полный период инвестиционной или финансово-кредитной операции.
Интервал начисления ( t ) – минимальный период, по прошествии которого производится начисление процентов по фиксированной ставке.
Проценты согласно договоренности между кредитором и заемщиком выплачиваются по мере их начисления или присоединяются к основной сумме долга (капитализация процентов).
Наращение (рост) инвестированной стоимости или первоначальной суммы – процесс увеличения инвестированных средств или суммы займа за счет присоединения начисленных процентов (дохода).
Наращенная сумма ( S )– первоначальная сумма капитала (P) с начисленными процентами в конце срока начисления.
Коэффициент (множитель, оператор) наращения (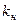 
) – величина, показывающая, во сколько раз выросла стоимость за определенный период.
Дисконтирование – операция определения суммы, которую необходимо инвестировать в заданный момент времени с тем, чтобы через некоторый период получить при установленном уровне ставки процента требуемую наращенную сумму.
Коэффициент (множитель, оператор) дисконтирования (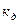 
) – величина, позволяющая при умножении на нее будущей стоимости получить текущий эквивалент данной стоимости.
Временная база (К)– основная единица времени, используемая в данном финансовом расчете для определения размерности процентной ставки. Она, как правило, равняется одному году и может варьироваться и приниматься равной 360, 365 или 366 дням.
Вопрос 2. Способы начисления процентов
И виды процентных ставок.
1. Декурсивный способ начисления процентов – это способ, при использовании которого проценты начисляются в конце каждого интервала начисления, а величина процентов определяется исходя из величины начального (предварительного) капитала.
Для этого применяется декурсивная процентная ставка.
Декурсивная процентная ставка (ссудный процент) ( i ) – отношение суммы начисленного за определенный интервал времени дохода к сумме, имевшейся на начало данного интервала.
Данный способ является наиболее распространенным.
2. Антисипативный способ (предварительный) начисления процентов – способ, при котором проценты начисляются предварительно, т.е. в начале каждого интервала начисления, и сумма процентов определяется исходя их конечной (наращенной) суммы.
Для этого применяется антисипативная процентная ставка.
Антисипативная (учетная) ставка ( d )– отношение суммы дохода, получаемого за определенный период, к сумме, имеющейся на конец этого периода (полученной или получаемой по прошествии этого периода).
D – дисконт, общая сумма процентов за весь конверсионный период.
Процентная ставка как параметр коммерческих контрактов может быть:
1. Постоянной (фиксированной).
2. Переменной (плавающей). В этом случае указывается не сама ставка, а изменяющаяся во времени база (базовая ставка) и размер надбавки к ней – маржи, определяющей размер риска.
В России применяются базовые ставки по рублевым межбанковским кредитам МИБОР. Размер маржи определяется рядом условий, в частности финансовым положением заемщика, сроком кредита и т.д.
Важное место в системе процентных ставок занимает ставка рефинансирования ЦБ РФ – ставка, по которой ЦБ выдает кредит коммерческим банкам.
В практических расчетах применяют дискретные проценты – проценты, начисляемые за фиксированные интервалы времени (год, полугодие и т.д.). Т.о. время рассматривается как дискретная переменная.
Также проценты могут быть простыми, сложными и непрерывными.
Дисконтирование.
,
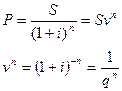
где v – дисконтный (учетный, дисконтирующий) множитель, обратный коэффициенту наращения.
Разность S – P, в случае, когда P определено дисконтированием, называют дисконтом.
Дисконтирование.
В этих случаях процесс дисконтирования происходит с замедлением, т.к. каждый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени.
Дисконтный множитель при этом равен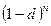 
.
Наращение.
.
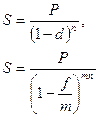
Множитель наращения при этом равен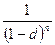 
.
Для периода начисления, не являющегося целым числом, множитель наращения будет определяться:
.
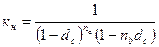
Для начисления процентов m раз в году наращенная сумма будет определяться:
Вопрос 8. Средние ставки.
В условиях нестабильности финансового рынка процентные ставки могут быть непостоянны во времени.
Если в финансовой операции размер процентной ставки изменяется, то все значения ставки можно обобщить с помощью средней процентной ставки. При этом замена всех усредненных значений ставок на среднюю процентную ставку не изменяет результатов наращения и дисконтирования.
Для ее нахождения составляется уравнение эквивалентности.
Пусть за последовательные периоды n1, n2, …, nk начисляются простые проценты по ставкам i1, i2, …, ik. Искомые средние можно получить путем приравнивания соответствующих множителей наращения:
.
,
где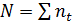 
— общий срок наращения процентов.
Найденный показатель представляет собой среднюю арифметическую взвешенную с весами, равными продолжительности отдельных периодов.
Если усредняются сложные переменные во времени ставки сложных процентов, то из равенства множителей наращения следует:
Средняя в этом случае вычисляется как взвешенная средняя геометрическая.
Средние ставки могут применяться и в однородных операциях, которые различаются суммами ссуд и процентными ставками.
Лекция № 1 . Способы начисления процентов и виды
Источник
Лекция. Простые и сложные проценты
Эти термины чаще всего встречаются в банковских делах, в финансовых задачах. Банки привлекают средства (вклады) за определенные процентные ставки. В зависимости от процентной ставки вычисляется доход.
Просмотр содержимого документа
«Лекция. Простые и сложные проценты»
Тема. Простые и сложные проценты
Эти термины чаще всего встречаются в банковских делах, в финансовых задачах. Банки привлекают средства (вклады) за определенные процентные ставки. В зависимости от процентной ставки вычисляется доход.
На практике применяются два подхода к оценке процентного дохода – простые и сложные проценты.
При применении простых процентов доход рассчитывается от первоначальной суммы вложенных средств не зависимо от срока вложения. В финансовых операциях простые проценты используются преимущественно при краткосрочных финансовых сделках, меньше года.
Пусть некоторая величина подвержена поэтапному изменению. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на начальном этапе. Так вычисляются простые проценты.
При применении сложных процентов накопленная сумма процентов добавляется во вклад по окончании очередного периода начислений. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. В этом случае имеем дело со “сложными процентами” (т.е. используются начисления “процентов на проценты”)
Первоначальная сумма и полученные проценты в совокупности называются накопленной (наращенной) суммой.
Так, если банковская ставка равна 10%, а первоначальная сумма 100 руб., то накопленная сумма за пять лет при применении простых и сложных процентов будет иметь вид:
Таблица 1. Накопленная сумма с использованием простых и сложных процентов.
Источник
Простые проценты
2.1 Определение простых процентов
Если сумма P увеличивается на r% , то полученная в результате сумма S называется наращенной суммой и вычисляется по формуле:
При этом величина P называется исходной суммой, а Pr — суммой начисленных процентов.
Пример 20. Сбербанк выплачивает по пенсионным вкладам 3.5% годовых (простые). Вычислим, какая сумма будет через год на счете пенсионера, положившего на счёт 1,200 руб. в начале года.
Решение. Через год на счету пенсионера будет сумма:
Если имеется несколько периодов времени, в каждый из которых исходная сумма P увеличивается на r% , то говорят, что на сумму P начисляются простые проценты. Наращенная сумма S , полученная в результате начисления n раз по r% на сумму P , выражается формулой:
Формула, выражающая наращенную сумму при начислении простых процентов, получена при условии, что число n периодов начисления процентов — целое. По определению мы введем такую же формулу для любого положительного (не обязательно целого) числа периодов, которое будем обозначать буквой t :
Необходимость начисления процентов за нецелое число периодов встречается в практике финансовых расчетов часто. Например, на депозит, пролежавший в банке 3 года и 3 месяца, банк должен начислить проценты за 3.25 периода.
Заметим, что при заключении финансовых контрактов обычно оговаривается наименьшая часть периода начисления процентов: например, каждый полный день (1/360 часть периода начисления, равного году). В этом случае t в формуле (2.1) принимает лишь значения соответственно k/360 или k/52 ( k — целое). Например, если депозит пролежал в банке 2 года 16 дней, то
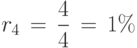
Для сравнения различных условий кредитования финансисты приводят ставку процента за произвольный период к годовой. Это правило в большинстве стран закреплено законом. Например, если банк даёт r% простых в год, то это соответствует квартальной ставке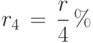 
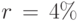
. Таким образом, при 
, имеем 
.
2.2 Разы и проценты
Когда в статистических отчётах, публицистике и в обыденной жизни сообщается об изменении какого-либо показателя, то это изменение в одних случаях указывается в процентах, а в других — в разах. И порой возникает путаница при переводе процентов в разы и разов в проценты.
Правило перевода предельно простое, если речь об увеличении (росте) некоторого показателя: при переводе процентов в разы надо, рассматривая процент как десятичную дробь, прибавить число 1; при переводе разов в проценты надо вычесть из разов 1 и результат перевести в проценты. Поясним на конкретных примерах, как получено и работает это правило.
Пример 21. На первой странице газеты «Ведомости» от 1 августа 2005 г. можно было увидеть заголовок: «Зарплата россиян за 1,5 года выросла в 1,5 раза». На сколько процентов увеличилась зарплата россиян за рассматриваемый период?
Решение. Обозначим через x среднюю зарплату в России в начале рассматриваемого периода (начало 2004 г.). Тогда из условия следует, что в конце рассматриваемого периода (середина 2005 г.) средняя зарплата составила 1.5x . Следовательно, зарплата увеличилась на
Мы так подробно расписали эти элементарные вычисления, чтобы было видно, что в круглой скобке из разов (1.5) вычитается 1. Переведем величину увеличения зарплаты в проценты от зарплаты в начале 2004 г.\ и получим, что зарплата увеличилась на 50%:
Рассмотрим теперь ситуацию, когда имеет место уменьшение некоторого показателя. Любое уменьшение можно считать ростом на отрицательное количество процентов. Для роста в таком понимании, если обозначить r . — величину роста, выраженную как десятичная дробь, то должно быть выполнено неравенство : 
. Это неравенство означает, что процент уменьшения не может быть больше 100%, а процент увеличения может быть неограниченно большим. Такому обобщению понятия роста поставим в соответствие понятие коэффициент изменения. Коэффициент изменения — положительное число, на которое надо умножить начальное значение показателя, чтобы получить его конечное значение . При увеличении значения показателя коэффициент изменения будет больше 1, а при уменьшении — меньше 1. С учетом сказанного, можно сформулировать единое правило перевода процентов в коэффициент изменения: при переводе процентов в коэффициент изменения нужно, рассматривая процент как десятичную дробь, прибавить 1.
Приведём схематичное изображение этого правила:
Пример 22. Цена акции уменьшилась за год на 20%. Вычислим, чему равен коэффициент изменения цены акции.
Решение. Обозначим через x цену акции в начале года. По условию цена акции в конце года составила
Следовательно, коэффициент изменения цены акции равен 0.8. Мы так подробно расписали эти элементарные вычисления, чтобы было видно, что в круглой скобке к процентам роста (-0.2) прибавляется 1.
Рассмотрим теперь ситуацию, когда имеет место уменьшение значения некоторого показателя x , которое выражается в разах. Предположим, что это значение уменьшилось в k раз. Это означает, что новое значение показателя равно x/k и составляет 1/k процентов от исходного значения. Соответственно, значение показателя изменилось на
Таким образом, при уменьшении значения некоторого показателя правило перевода разов в проценты может быть сформулировано следующим образом: при переводе k разов в проценты нужно выразить в процентах дробь (k-1)/k .
Приведем теперь схематичное изображение общего правила перевода разов в проценты:
Пример 23. За 2 года цена некоторой модели цифрового фотоаппарата уменьшилась в 3 раза. Вычислим, на сколько процентов уменьшилась цена.
Решение. Используем приведенное выше правило перевода при k=3 :
Следовательно, за 2 года цена фотоаппарата уменьшилась на 66.67%.
Источник
