Цифровая модуляция
Сведения о системах модуляции
В настоящее время все абонентские терминалы преобразуют сигналы в цифровую форму. Одна из важнейших проблем, как на абонентском участке, так и участке соединительных линий обеспечить максимальную скорость передачи цифровой информации.
Существующая абонентская проводная сеть имеет громадный объем. Замена ее на более скоростную среду передачи, например, на оптоволоконную среду, подобна замене песка на всех пляжах мира и не всегда возможна по экономическим причинам.
Поэтому основная задача, которую успешно решают связисты мира увеличение пропускной способности существующей.
Всегда возникает основной вопрос, телефонная связь уже существует более 150 лет. Эта проводная сеть рассчитана на диапазон человеческого голоса или точнее на пропускание аналоговой частоты в диапазоне от 0,3 до 3,4 кГц.
Как же удалось сегодня многократно увеличить этот диапазон и сделать возможным передачу информации, которая требует ресурс в более чем 100 раз. Это достигнуто различными способами, но в основном благодаря разработке способов модуляции.
Наиболее применяемый в настоящее время класс модуляции фазовый. Мы постепенно рассмотрим этот вид. Начиная от простейших видов такой модуляции, а потом рассмотрим наиболее применяемые методы.
Многоуровневая передача сигналов
Цифровое преобразование сигналов подразумевает двоичное кодирование сигналов. Когда же нужно получить высокую скорость передачи данных в условиях ограниченной полосы прибегают к методам повышения информационной емкости передаваемых символов. Одним из таких методов является многоуровневая система, когда каждый сигнал может принимать несколько уровней амплитуды в зависимости от значения исходного символа. Скорость передачи данных в многоуровневой системе передачи равна.
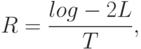 | ( 4.1) |
– уровней, которые могут быть выбраны для передачи сигналов в данном интервале,
–длительность интервала сигнала.
Скорость передачи сигнала, равная 
На рис.4.1 показан пример восьмиуровневого сигнала. Это позволяет увеличить скорость передачи 3 бита на сигнальный интервал (т.е. 3 бита на бод).
Многоуровневые передающие системы увеличивают скорость передачи данных в пределах заданной полосы частот, но требуют значительного увеличения уровня сигнал шум. Известно, что при большом уровне помех наиболее уязвима амплитуда сигнала. Поэтому такая система не получила распространения.
В современных системах примером применения такой системы может служить организация цифровой абонентской линии в системе ISDN (Integrated Services Digital Network ), в которой для достижения скорости 160 кбит/с. используется четырехуровневая передача [ 2 ]
Фазовые методы модуляции
Фазовые методы модуляции XE «Фазовые методы модуляции » являются, в какой — то степени аналогами многоуровневой передачи сигналов, поскольку тоже позволяют увеличить информационную емкость передаваемого символа.
Фазовая манипуляция
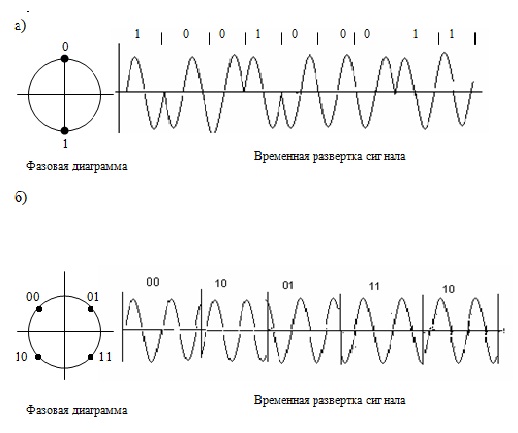
Фазовая модуляция связана с манипуляцией фазы. При такой манипуляции для получения бинарного сигнала в каждом тактовом интервале используется одна из фаз, отличающаяся на 180 градусов.
Возможна также многоуровневая ФМ. Фазовая манипуляция XE «Фазовая манипуляция» в настоящее время – наиболее распространенная форма модуляции.
Популярность этого типа модуляции определяется, прежде всего, наличием постоянной огибающей, что обеспечивает то, что она нечувствительна к изменениям уровня сигнала, влиянию затухания и характеристикам аппаратуры усиления и обеспечивает хорошую характеристику. С точки зрения отношения сигнал шум (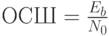
Общий вид n-уровневой фазовой манипуляции отображается формулой
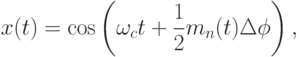 | ( 4.1) |
-величина, на которую отличаются фазы соседних сигналов;
— симметричный n –уровневый сигнал «без возвращения к нулю» ( NRZ – non return to zero) c уровнями
и т.д.
На рис.4. 2 показаны примеры типичных 2-ФМ и 4-ФМ – сигналов. На рисунке скорость передачи при 4-ФМ, в два раза меньше, чем 2-ФМ, что обеспечивает одинаковую скорость передачи данных (из-за увеличения информационной емкости). На этом рисунке приведены фазовые диаграммы для косинусоидального сигнала (см. формулу 4.1).
Источник
3. Цифровые способы модуляции
3.1. Предварительные замечания
В технике цифровой связи методы модуляции играют весьма значимую роль. Помимо своей основной функции — преобразования символ-сигнал — процесс модуляции является составной частью общего процесса согласования сигнала с характеристиками канала. Современные методы многопозиционной модуляции в полном соответствии с теоремой Шеннона могут рассматриваться и как способ кодирования данных сообщения в символы канала.
Свойства цифрового сигнала не позволяют передавать такой сигнал по каналу связи непосредственно, то есть «в первичной полосе частот» из-за слишком высокой скорости передачи, оцениваемой в сотни мегабит в секунду. Кроме того, существующие сети ТВ вещания (спутниковые, кабельные или наземные), как правило, построены по принципу частотного уплотнения. Поэтому сигнал, предназначенный для передачи по таким сетям, должен быть точно ориентирован в принятой системе организации частотных каналов. Следует также иметь в виду, что передаваемый сигнал должен быть энергетически сосредоточен в определенной ограниченной области спектра. Как правило, несущей (модулируемой) частотой является гармонический сигнал. Изменяемыми параметрами в таком случае могут быть его амплитуда, частота и фаза. Если модулирующий сигнал имеет цифровую природу и изменяется дискретно, принимая фиксированные значения, то понятие «модуляция» иногда заменяется понятием «манипуляция».
Передаваемый сигнал, таким образом, в результате модуляции можно представить в следующей форме
U(t) = (Амплитуда)cos[2π(Частота)t + (Фаза)]. (3.1)
Использование для передачи сигналов цифрового телевидения различных видов модуляции позволяет одновременно увеличить количество передаваемой информации в единицу времени, сократить используемую полосу частот и повысить помехоустойчивость ТВ системы. В цифровом телевидении может применяться амплитудная модуляция (AM), в иностранной литературе применительно к цифровому сигналу называемая ASK (Amplitude Shift Keying); частотная модуляция (ЧМ), ее обозначают также FSK (Frequency Shift Keying), и фазовая модуляция (ФМ), англоязычное обозначение PSK (Phase Shift Keying).
На рисунке 3.1 иллюстрируется принцип работы каждого из применяемых видов модуляции для двухпозиционного модулирующего сигнала, то есть когда каждое состояние сигнала передает один бит информации. На рисунке 3.1 также показаны графики, поясняющие изменение сигнала во времени.
Рисунок 3.1 — Виды модуляции при двухпозиционном модулирующем сигнале
Демодуляция рассмотренных сигналов достаточно проста в техническом отношении, и для ее осуществления известно много способов. Качество того или иного способа модуляции при передаче цифровых сигналов оценивается обычно по следующим критериям:
эффективности использования частотного спектра;
минимально необходимого отношения сигнал-помеха;
стойкости к ухудшению условий приема на отдельных частотах.
Эффективность использования частотного спектра увеличивается с увеличением числа состояний, которые может принимать сигнал при передаче одного символа. Если модулирующим сигналом является сигнал, в котором каждый символ передается не двумя, а большим количеством возможных его значений, то количество информации, передаваемое с каждым символом, возрастает. Такие значения обычно выбираются равными 4, 16, 32, 64, 128 и т.д., то есть как ряд 2 n , где n — число возможных состояний передаваемого или модулирующего сигнала во время передачи одного символа.
Эта эффективность оценивается величиной, измеряемой в битах в секунду на один герц (бит/с/Гц). Такая размерность показывает, что в данном случае оценивается скорость потока, приходящаяся на единицу частоты.
Чем выше количество информации, переносимое одним символом, тем выше число возможных состояний, которое может принять изменяемый в процессе модуляции параметр модулируемого сигнала (виды модуляции с большим числом таких состояний называют многопозиционными), и соответственно тем выше эффективность использования частотного спектра. Однако, чем большее число состояний может принимать модулирующий сигнал, тем меньше существует отличий в параметрах этих состояний, а значит, демодуляция такого сигнала в условиях помех может стать затруднительной. Поэтому эффективность использования частотного спектра обычно связана с возможно достижимым отношением сигнал/помеха, и при выборе этих параметров необходим компромисс.
Источник
Способы модуляции при передаче цифровой информации
Лет 15 тому назад один из бывших сотрудников ведущего европейского поставщика оборудования связи (Ericsson) рассказывал мне, как они поставляли систему радиодоступа DECT в одну из российских «электросвязей». Когда шведы приехали подписывать контракт, то главный инженер российского оператора во время церемонии подписания вдруг произнёс: «Что-то мне кажется, вы нас обманываете – как это можно голос в цифре передавать, да ещё по воздуху?». Немая сцена…
Вот и попробуем разобраться, как «голос преобразуется в цифру».
Методы модуляции аналоговых сигналов
Любой аналоговый сигнал, например, электрический ток из микрофона, при передаче по цифровым каналам связи нужно, как говорят, «оцифровать». То есть, выполнить цифровую модуляцию. Можно, конечно, и в аналоговом виде сигнал передавать, но с середины прошлого века так уже никто не делает – это чревато высокими затратами и очень низким качеством связи.
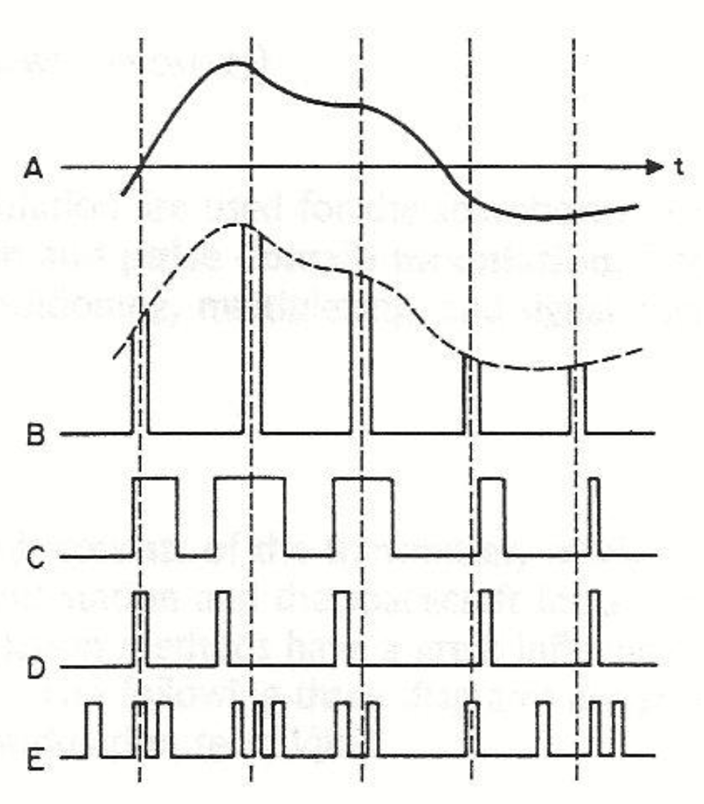
Для оцифровки аналоговый сигнал А (рис. 1) нужно подвергнуть модуляции. Например, существует Импульсно-Амплитудная Модуляция (ИАМ), по-английски PAM (Pulse Amplitude Modulation), что показано на графике В. По сути, это просто выборка (дискретизация) значений амплитуды сигнала через равные промежутки времени. В результате сигнал все равно остаётся аналоговым, только представленным в виде «столбиков», высота которых представляет собой амплитуду сигнала в момент выборки.
Теперь по одному проводу можно передавать несколько сигналов, если в промежутке между двумя выборками сигнала А передавать выборки от других сигналов.
Другой вид модуляции — широтно- импульсная модуляция (ШИМ), или PWM — Pulse Width Modulation, что мы видим на графике С. Здесь амплитуда А сигнала в каждый момент выборки представлена длительностью («шириной») импульсов, амплитуда которых всегда постоянная.
На графике D показана фазовая модуляция, или PPM — Pulse Position Modulation. Дословно сиё переводится как «модуляция по положению импульса». Фактически, амплитуда сигнала А здесь представлена фазой (сдвигом) импульсов равной амплитуды относительно момента дискретизации исходного сигнала А.
Ну и наконец, есть ещё импульсно-кодовая модуляция (ИКМ), которая показана на графике Е. По-английски она называется PСM (Pulse Сode Modulation).
Вот эта модуляция нас и будет больше всего интересовать, поскольку она и есть цифровая!
Рис. 1. Виды модуляции аналогового сигнала.
Заметим, что и цифровой сигнал тоже можно различным образом модулировать.
Преобразование аналогового сигнала в цифровой
Чтобы преобразовать аналоговой сигнала в цифровую форму, нужно его, во-первых, сделать выборку его величины (амплитуды) через равные промежутки времени. Это процесс называется «семплированием» (от слова sample – «образец») и показан на рис. 2.
Рис. 2. Преобразование аналогового сигнала в цифровой
Во-вторых, нужно сделать квантование, т.е. измерение величины амплитуды сигнала в моменты выборки и округление результата измерения до ближайшего значения ступени квантования.
И в-третьих, полученные кванты нужно представить в цифровой форме, т.е. закодировать тем или иным способом. На рисунке 2 показано кодирование в виде трёхразрядного (трёхбитового) двоичного числа. Вообще, этого очень мало, на практике обычно применяют 8-битное кодирование. Поэтому, как видим, полученный результат довольно сильно отличается от формы исходного сигнала.
Что нужно, чтобы повысить точность, т.е. соответствие полученных значений исходному сигналу? Очевидно, нужно увеличить частоту семплирования. То есть, чаще производить выборку. Здесь можно воспользоваться теоремой, у которой аж целых три автора: два зарубежных, Найквист и Шэннон, и наш, российский Котельников. Поэтому в России эту теорему называют теоремой Котельникова, а за рубежом – Найквиста-Шэннона. И гласит эта теорема следующее: «сигнал, спектр которого ограничен частотой среза (fср), может быть восстановлен без потерь, если частота дискретизации составляет не менее fд = 2fср». То есть, берём самую высокую гармонику сигнала (как известно, сигнал любой практически формы можно разложить на сумму синусоидальных гармоник с различными амплитудами), и умножаем её на два. После этого, можем считать, что мы адекватно преобразовали аналоговый сигнал в цифровую форму. Ну, если не считать т.н. «шумов квантования», о которых речь немного позже.
Например, если частотный диапазон телефонного сигнала ограничен частотой 3400 Гц (а он именно такой частотой и ограничен, на входе ставят частотный фильтр), то частота выборки (семплирования) должна быть не менее 6800 Гц. На практике обычно делают семплирование с частотой 8000 Гц.
И ещё, как уже отмечалось, нужно повысить разрядность кодирования, то есть кодировать выборки не трёхразрядным двоичным числом, а восьмиразрядным (байтом).
Восстановление формы исходного аналогового сигнала на приёмном конце линии связи
Затем, полученный цифровой сигнал передают тем или иным способом по линии связи. Как это делается, нас пока не интересует. Однако, на приёмном конце линии связи форму сигнала нужно восстановить. Вот что при этом получается (рис. 3).
Рис. 3. Восстановление исходной аналогового формы сигнала.
Как видим, при трёхразрядном кодировании (семь уровней квантования) исходную форму сигнала удаётся восстановить лишь приблизительно. На рис. 3. даже на глаз видны существенные различия полученного сигнала от исходного, хотя общая форма сигнала похожа. Например, если исходный аналоговый сигнал представляет речь, то собеседник на приёмном конце при этом сможет понять, о чем его визави говорит, но тембр голоса может сильно измениться, и возможно, некоторые слова придётся повторять.
Шумы квантования
При квантовании аналогового сигнала, как показано на рис.1, реальное значение сигнала заменяется ближайшим ему уровней квантования. При этом, реальная волнообразная форма аналогового сигнала заменяется «лесенкой», ступени которой соответствуют уровням квантования.
Рис. 4. Аппроксимация аналогового сигнала уровнями квантования.
Ясно, что такая «пилообразная» кривая отличается от исходной формы аналогового сигнала. Различие (ошибка) между аналоговым сигналом и его ступенчатой аппроксимацией и есть шумы квантования.
Чем больше уровней квантования, тем точнее аппроксимация аналогового сигнала при квантовании, что видно на рис. 5.
Рис. 5. Точность аппроксимации повышается с увеличением числа уровней квантования.
Импульсно-кодовая модуляция ИКМ (PCM, Pulse Code Modulation)
Импульсно-кодовая модуляция – и есть цифровизация аналогового сигнала, то есть, представление аналогового сигнала, вернее его квантованных значений, в цифровой форме. По линии связи при этом передаётся последовательность нолей и единиц (битов), которая представляет собой двоичное число, равное значению уровня квантования в момент квантования.
Рис. 6. Принцип импульсно-кодовой модуляции ИКМ (источник: Н.Н. Слепов. Современные технологии цифровых оптоволоконных сетей связи, 2000 г.).
Квантование, в соответствии с теоремой Котельникова (или Шеннона-Найквиста), производится с частотой 8000 Гц, то есть период квантования составляет 125 мкс. Длительность передачи 8-битового кода выборки квантования составляет 3,91 мкс.
Почему именно 8000 Гц? Потому, что частота среза в телефонном канале составляет 3400 Гц. С «запасом прочности» величина частота среза выбрана равной 4000 Гц, поэтому частота дискретизации выбрана 8000 Гц.
Методы двоичного кодирования.
Двоичное кодирование сигнала для передачи его по каналам связи производится различными методами.
Рис. 7. Методы двоичного кодирования.
- Самый простой метод кодирования — униполярный код NRZ (Non-Return to Zero), «без возврата к нулю». Единица представлена высоким уровнем сигнала, тока или напряжения, ноль – нет тока, либо напряжения. Впрочем, может быть и наоборот, это непринципиально.
- Биполярный код NRZ (Non-Return to Zero), «без возврата к нулю». Единица представлена положительным значением тока в цепи, ноль – отрицательным.
- Униполярный код RZ (Return to Zero) «с возвратом к нулю». После обозначения единицы, сигнал в течение периода такта возвращается к нулевому значению сигнала (не ноля, как числа, а лишь величины модулирующего сигнала).
- Биполярный код RZ (Return to Zero) «с возвратом к нулю». То же самое, только две идущие подряд единицы обозначаются разнополярными импульсами с чередованием. Ноль обозначается отсутствием тока или напряжения.
- И наконец, самый экстравагантный код – «Манчестерский» (Manchester Code). Читателю предлагается самому разобраться в методе кодирования по рисунку.
Дилемма между сильным и слабым сигналом
Метод ИКМ не лишен недостатков. Кроме шумов квантования, есть ещё и проблема возрастания ошибок квантования, если сигнал имеет низкую амплитуду. В случае телефонного разговора, это будет означать, что если собеседник будет говорить негромко, то его речь может стать совсем неразборчивой.
Рис. 8. Линейное и нелинейное кодирование.
Это может произойти при линейном кодировании, когда все уровни квантования имеют одинаковый шаг по амплитуде сигнала. На рис. 8 видно, что при линейном квантовании слабый сигнал сильно искажается.
Поэтому применяется нелинейное кодирование (компандирование) сигнала.
Компандирование: А-закон и μ-закон
Существует два метода компандирования: А-закон (используется в Европе и России) и μ-закон (используется в Северной Америке и Японии).
А-закон командирования выглядит, как показано на рис. 9, и выражается следующей математической формулой:
Рис. 9. А-закон компандирования
В правой части рис. 9 показана кривая А-закона только для положительных значений входного сигнала. Такая же кривая имеется для отрицательных значений, которая будет «смотреть» вниз.
По вертикальной оси отложено 128 ступеней квантования. Если учесть нижнюю часть кривой, ступеней будет 256. В двоичной форме число 256 можно представить байтом из 8 разрядов. Принцип кодирования показан в таблице в левой части рисунка 9.
При 256 ступенях квантования можно обеспечить довольно хорошее соответствие квантованных значений сигнала его исходной кривой.
Компандирование сигнала и формула μ-закона показано на рисунке 10. Принципиальных отличий от А-закона здесь нет.
Рис. 10. Компандирование по μ-закону.
При восстановлении аналогового сигнала из цифровой формы на стороне приёма выполняется обратное компандирование, таким образом, удаётся получить довольно хорошее соответствие полученного сигнала исходному за счёт двух факторов:
- Достаточного количества уровней квантования – 256 (2 8 )
- Применения компандирования, которое обеспечивает достаточно хорошее качество передачи сигналов малой амплитуды.
В следующей статье Ликбеза рассмотрим методы формирования цифровых трактов.
— Ты прошёл через мой беспроводной цифровой поток и промодулировался!
Источник

 – уровней, которые могут быть выбраны для передачи сигналов в данном интервале,
– уровней, которые могут быть выбраны для передачи сигналов в данном интервале, –длительность интервала сигнала.
–длительность интервала сигнала.
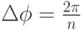 -величина, на которую отличаются фазы соседних сигналов;
-величина, на которую отличаются фазы соседних сигналов;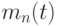 — симметричный n –уровневый сигнал «без возвращения к нулю» ( NRZ – non return to zero) c уровнями
— симметричный n –уровневый сигнал «без возвращения к нулю» ( NRZ – non return to zero) c уровнями  и т.д.
и т.д.