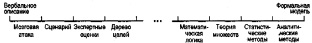Научная электронная библиотека
Оразбаев Б. Б., Курмангазиева Л. Т., Коданова Ш. К.,
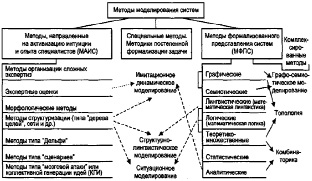
3.4. Методы моделирования систем
1. Общие подходы к моделированию систем.
2. Аналитические и статистические методы.
3. Математическая логика.
4. Лингвистические и семиотические представления.
5. Графические методы.
6. Методы, направленные на активизацию использования интуиции и опыта специалистов.
1. Общие подходы к моделированию систем
Постановка любой задачи заключается в том, чтобы перевести её словесное, вербальное описание в формальное. В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается её адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.
По мере усложнения задач получение модели и доказательство её адекватности усложняется. Вначале эксперимент становится дорогим и опасным (например, при создании сложных технических комплексов, при реализации космических программ и т.д.), а применительно к экономическим объектам эксперимент становится практическим нереализуемым, задача переходит в класс проблем принятия решений, и постановка задачи, формирование модели, т.е. перевод вербального описания в формальное, становится важной составной частью процесса принятия решения.
Перевод вербального описания в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы.
Для решения проблемы перевода вербального описания в формальное описание в различных областях деятельности стали развиваться специальные приёмы и методы. Так, возникли методы типа «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.
В свою очередь, развитие математики шло по пути расширения средств постановки и решения трудноформализуемых задач. Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределённости инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, теорию нечетких множеств, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределённостью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.
Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился как бы «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот спектр условно представлен на рис. 3.4, а.
Рис. 3.4. Модели и моделирование систем
Развитие методов моделирования, разумеется, шло не так последовательно, как показано на рис. 3.4, а. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов. Их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации (в основном – для формальных методов). Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп. Однако основную идею – существование «спектра» методов между вербальным и формальным представлением проблемной ситуации – рис. 3.4, а иллюстрирует.
Первоначально исследователи, развивающие теорию систем, предлагали классификации систем и старались поставить им в соответствие определённые методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики.
Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (отображать разными классами систем и соответственно различными моделями, организуя таким образом как бы процесс постепенной формализации задачи, т.е. «выращивание» её формальной модели. Подход помогает понять, что неверно выбранный метод моделирования может привести к неверным результатам, к невозможности доказательства адекватности модели, к увеличению числа итераций и затягиванию решения проблемы.
2. Аналитические и статистические методы
Аналитические и статистические методы получили наибольшее распространение в практике проектирования и управления. Для представления промежуточных и окончательных результатов моделирования широко используются графические представления (графики, диаграммы и т.п.). Однако последние являются вспомогательными; основу же модели, доказательства её адекватности составляют те или иные направления аналитических и статистических представлений. Поэтому, несмотря на то, что по основным направлениям этих двух классов методов в вузах читаются самостоятельные курсы лекций, мы всё же кратко охарактеризуем их особенности, достоинства и недостатки с точки зрения возможности использования при моделировании систем.
Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек (безразмерных в строгих математических доказательствах), совершающих какие-либо перемещения в пространстве или взаимодействующих между собой.
Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.).
Аналитические представления имеют многовековую историю развития, и для них характерно не только стремление к строгости терминологии, но и к закреплению за некоторыми специальными величинами определённых букв (например, удвоенное отношение площади круга к площади вписанного в него квадрата π ≈ 3,14; основание натурального логарифма – е ≈ 2,7 и т.д.).
На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной науки – исследования операции, системный анализ, как математическое программирование (линейное, нелинейное, динамическое и т.п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.п.).
Эти теоретические направления стали основой многих прикладных, в том числе теории автоматического управления, теории оптимальных решений и т.д.
При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.
Большинство из направлений математики не содержат средств постановки задачи и доказательства адекватности модели. Последняя доказывается экспериментом, который по мере усложнения проблем становится также всё более сложным, дорогостоящим, не всегда бесспорен и реализуем.
В то же время в состав этого класса методов входит относительно новое направление математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей (стохастическое, нечеткое программирование).
Статистические представления сформировались как самостоятельное научное направление в середине прошлого века (хотя возникли значительно раньше). Основу их составляет отображение явлений и процессов с помощью случайных (стохастических) событий и их поведений, которые описываются соответствующими вероятностными (статистическими) характеристиками и статистическими закономерностями.
Статистические отображения системы в общем случае (по аналогии с аналитическими) можно представить как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (её учитываемые в модели свойства) оператор Ф[Sx]. «Размытую» точку следует понимать как некоторую область, характеризующую движение системы (её поведение); при этом границы области заданы с некоторой вероятностью p («размыты») и движение точки описывается некоторой случайной функцией.
Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а–b, смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трёхмерную и т.д. картины статистического распределения.
Статистические закономерности можно представить в виде дискретных случайных величин и их вероятностей, или в виде непрерывных зависимостей распределения событий, процессов.
Для дискретных событий соотношение между возможными значениями случайной величины xi и их вероятностями pi, называют законом распределения и либо записывают в виде ряда (табл. 3.1), либо представляют в виде зависимостей F(x) (рис. 3.5, а) или p(х) (рис. 3.5, в).
Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения – рис. 3.5, б), либо в виде плотности вероятностей (дифференциальный закон распределения – рис. 3.5, г). В этом случае 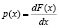
Для полной группы несовместных событий имеют место условия нормирования:
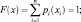
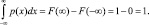
Часто применяют тот или иной вид зависимостей, приведенных на рис. 3.5, более подходящий для соответствующих приложений.
Источник
Методы моделирования сложных систем
Цель работы
Целью первой части работы является изучение новых явлений в существенно квантовых системах, интересных с фундаментальной точки зрения и перспективных для приложений. В частности, планировалось моделирование ряда квантовых явлений на современных квантовых компьютерах и анализ ограничений такого моделирования, связанных с ошибками работы квантовых гейтов и с одно- и многокубитной декогеренцией. Планировался анализ возможностей реализации аналогов эффектов квантовой электродинамики в сверхпроводниковых системах, а также поиск новых эффектов в системах связанных кубитов и резонаторов. Была поставлена цель изучить влияние координатной зависимости эффективных масс фотонов и поляритонов на свойства бозе-конденсата таких частиц. Также планировалось исследование низкотемпературной системы бозонов с дальнодействующим межчастичным потенциалом.
Целью второй части данной работы является исследование спектральные свойства коннектомов и их особенности у разных организмов. Также необходимо изучить вопрос о том, какие именно особенности строения нервных сетей приводят к отличиям их спектров от спектров всех остальных сетей, а также насколько эти особенности зависят от видовых различий между организмами.
Целью третьей части работы является, во-первых, исследование течения стратифицированной жидкости c быстроосциллирующей границей раздела при неустойчивости Рэлея-Тейлора и ее асимптотическое поведение при стремлении частоты осцилляций к бесконечности в предположении, что сила тяжести преобладает над вязкостью, и относительная разница между плотностями жидкостей мала. Во-вторых, целью работы является создание общего алгоритма для построения формальных асимптотических решений рассматриваемых задач, основанного на современных методах исследования сложных задач математической физики. Эта задача возникла из-за обнаруженных в классических работах по трехпалубной структуре (в которых была рассмотрена только задача обтекания локализованной неровности) неточностей построения решения, приводящие к уравнению Бенджамина, в котором отсутствует связь как с геометрией задачи, так и с функциями, описывающими течения в многопалубной структуре). Очевидно, что такое уравнение лишено всякого гидродинамического смысла.
Цель четвертой части работы состоит в исследование квантовых резонансно-интегрируемых систем. Исследование туннельных эффектов в гиперболической ловушке с резонансом частот, когда гамильтониан является зеркально симметричным: построение эффективного гамильтониана, выявление условий возникновения биорбитальных состояний, представление туннельного расщепления в терминах комплексификации фазового пространства классической механической системы. Исследование геометрических токов в искривлённом тонком слое при совпадение циклотронной частоты с частотой поперечных колебаний заряда, определение влияния геометрии слоя на направление индуцированного тока. Также исследуются общие алгебраические методы сведения задачи с резонансами к гамильтониану с неприводимым резонансом.
Используемые методы
Экспериментальное моделирование квантовых спиновых систем проводилось удаленно на квантовом процессоре IBMqx4, для его анализа использовалось теоретическое моделирование на основе аналитических и численных квантовомеханических расчетов. Моделирование динамики связанных систем кубитов и резонаторов проводилось численным решением уравнения Линдблада в походящем базисе состояний. Анализ бозе-конденсации фотонов и поляритонов проводился путем численного решения уравнения Гросса-Питаевского. Система бозонов с дальнодействующим межчастичным потенциалом моделировалась численно диффузионным методом Монте Карло. Для режима слабого взаимодействия была разработана специальная модификация метода Боголюбова.
Для моделирования коннектома использовались различные компьютерные методы, включающие вероятностные методы Монте-Карло и различные алгоритмы на графах в том числе алгоритмы поиска сообществ, алгоритмы хранения и работы с большими данными, различные алгоритмы визуализации сетей и алгоритмы распространения возбуждения на сетях. Для анализа свойств коннектома, смоделированных сетей и случайных сетей использовался весь стандартный набор методов статистической физики, включая метод производящей функции, кластерный анализ, методы, разработанные для анализа аномальной диффузии, теория случайных матриц.
Основным приемом исследования гидродинамических задач является мало используемый факт, состоящий в том, что осреднение можно понимать, как предел в смысле обобщенных функций. Отсюда сразу следует, что осреднение – локальная операция, и возможность использования при осреднении всего аппарата теории обобщенных функций. Метод построения асимптотических решений задач обтекания основан на комбинации метода погранслойного разложения и метода осреднения (для случая периодических неровностей) или варианта метода Маслова-Уизема (для случая локализованных неровностей).
При исследование квантовых резонансно-интегрируемых систем используются алгебраические и геометрические методы: алгебраическое усреднение, построение резонансных алгебр симметрий, выделение в них структуры рождение-уничтожение, анализ топологии симплектических листов и классических траекторий движения. Применяются методы дискретного и непрерывного квазиклассического ВКБ приближения.
Эмпирическая база исследования
В качестве эмпирической базы использовались результаты исследований по тематике проекта, опубликованные в мировой научной литературе.
Результаты работы
В первой части работы было проведено экспериментальное моделирование квантовой эволюции систем нескольких связанных спинов, в результате чего продемонстрированы эффекты квантовой запутанности и блокады передачи возбуждений. Выявлены ограничения на длину квантовых алгоритмов, обусловленных ошибками срабатывания квантовых гейтов. Предложена новая реализация динамического эффекта Лэмба в сверхпроводниковых системах. Обнаружен интересный эффект усиления квантовых явлений в одной подсистеме за счет диссипации энергии в другой подсистеме. Изучено влияние координатной зависимости эффективной массы фотонов и поляритонов на энергии и волновые функции их бозе-эйнштейновских конденсатов в оптических микрополостях. Показано, что при помощи координатной зависимости эффективной массы можно управлять силой взаимодействия частиц, и даже менять их отталкивающее взаимодействие на притягивающее. Детально исследованы свойства квантовой системы бозонов при нулевой температуре с отталкивающим потенциалом взаимодействия, обратно пропорциональным квадрату расстояния. Обнаружен фазовый переход между газовой и твердой фазами, происходящий при критической силе взаимодействия. При слабой силе связи найден плазмонный спектр возбуждений с корневой дисперсией.
Основные результаты второй части работы можно сформулировать следующим образом. Во-первых, коннектом человека демонстрирует существенную неслучайность по сравнению с сетями других животных. Это может указывать на эволюционный отбор, действующий на нервную сеть. Во-вторых, локальная кластеризация во многом определяет форму спектра коннектома и, следовательно, играет важную роль в структуре исследуемых сетей. Такая особенность может вытекать из «модульной», иерархической организации сетей мозга
Результатом третьей части работы является, во-первых, система уравнений, регуляризующая известные уравнения Дарси в том смысле, что в устойчивом случае регуляризованная система переходит в систему уравнений Дарси, а при неустойчивости Рэлея-Тейлора описывает развитие зоны перемешивания. Во-вторых, в третьей части работы получены формальные асимптотические решения нестационарных задач обтекания локализованных и периодических неровностей на пластине. Важным результатом является то, что полученное в результате предложенного подхода уранвнеие типа Бенджамина-Оно содержит в себе члены, описывающие геометрию задачи. Более того, оказалось, что это уравнение является автоматически удовлетворяемым соотношением, а сама неизвестная функция может быть найдена из краевого условия для системы уравнений типа Прандтля с индуцированным давлением, описывающей течение в пристеночной области.
В результате четвертой части работы исследован общий гамильтониана резонансной гиперболической ловушки с парой совпадающих частот. Показано, что если ангармоническая часть гамильтониана гиперболической ловушки является зеркально симметричной, то эффективный гамильтониан имеет неустойчивые равновесия и сепаратрисы, определяющие отдельные классически допустимые области в пространстве первых интегралов идеальной ловушки. Соответствующие стационарные состояния удерживаемого заряда могут образовывать биорбитальные состояния, то есть состояние, локализованное на двух разных классических траекториях. Получена квазиклассическая асимптотика расщепления энергий, соответствующую туннелированию заряда между этими двумя траекториями в фазовом пространстве. Квазиклассическая асимптотика туннельного расщепления представлена в терминах комплексных периодических инстантонов. В задаче о частице в тонком искривленном слое при магнитно-размерном резонансе изучено взаимодействие индуцируемых токов в общем виде, а также для слоев цилиндрической и параболической формы. Приведен пример формы слоя, при которой эффект Холла будет подавлен возникающими геометрическими токами, а также слой, ток в котором индуцируется в направлении приложенного к нему электрического поля.
Представлен алгебраический метод приведения задачи с частотными резонансами общего вида к неприводимым резонансам. Построены образующие алгебры симметрий, неприводимые представления и когерентные состояния в этом случае.
Степень внедрения, рекомендации по внедрению или итоги внедрения результатов НИР
Анализ работы 5- и 16-кубитных квантовых компьютеров позволил разработать эвристические модели, с помощью которых можно извлекать значимую информацию даже из результатов работы квантового компьютера, искаженных неидеальностью срабатывания гейтов. Предложенная реализация динамического эффекта Лэмба в связанной системе сверхпроводникового кубита и резонатора может быть осуществлена экспериментально. Предсказанные эффекты координатно-зависимой эффективной массы фотонов и поляритонов также могут быть проверены в современных экспериментах. Исследованные системы бозонов с дальнодействующим отталкиванием могут быть реализованы на базе нескольких физических систем.
Результаты, полученные при исследовании резонансных квантовых систем, могут быть использованы при проектировании и разработке перспективных нано-электронных устройств.
Источник