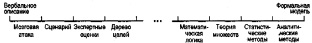Научная электронная библиотека
Оразбаев Б. Б., Курмангазиева Л. Т., Коданова Ш. К.,
3.4. Методы моделирования систем
1. Общие подходы к моделированию систем.
2. Аналитические и статистические методы.
3. Математическая логика.
4. Лингвистические и семиотические представления.
5. Графические методы.
6. Методы, направленные на активизацию использования интуиции и опыта специалистов.
1. Общие подходы к моделированию систем
Постановка любой задачи заключается в том, чтобы перевести её словесное, вербальное описание в формальное. В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается её адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.
По мере усложнения задач получение модели и доказательство её адекватности усложняется. Вначале эксперимент становится дорогим и опасным (например, при создании сложных технических комплексов, при реализации космических программ и т.д.), а применительно к экономическим объектам эксперимент становится практическим нереализуемым, задача переходит в класс проблем принятия решений, и постановка задачи, формирование модели, т.е. перевод вербального описания в формальное, становится важной составной частью процесса принятия решения.
Перевод вербального описания в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы.
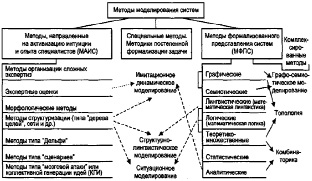
Для решения проблемы перевода вербального описания в формальное описание в различных областях деятельности стали развиваться специальные приёмы и методы. Так, возникли методы типа «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.
В свою очередь, развитие математики шло по пути расширения средств постановки и решения трудноформализуемых задач. Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределённости инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, теорию нечетких множеств, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределённостью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.
Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился как бы «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот спектр условно представлен на рис. 3.4, а.
Рис. 3.4. Модели и моделирование систем
Развитие методов моделирования, разумеется, шло не так последовательно, как показано на рис. 3.4, а. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов. Их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации (в основном – для формальных методов). Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп. Однако основную идею – существование «спектра» методов между вербальным и формальным представлением проблемной ситуации – рис. 3.4, а иллюстрирует.
Первоначально исследователи, развивающие теорию систем, предлагали классификации систем и старались поставить им в соответствие определённые методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики.
Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (отображать разными классами систем и соответственно различными моделями, организуя таким образом как бы процесс постепенной формализации задачи, т.е. «выращивание» её формальной модели. Подход помогает понять, что неверно выбранный метод моделирования может привести к неверным результатам, к невозможности доказательства адекватности модели, к увеличению числа итераций и затягиванию решения проблемы.
2. Аналитические и статистические методы
Аналитические и статистические методы получили наибольшее распространение в практике проектирования и управления. Для представления промежуточных и окончательных результатов моделирования широко используются графические представления (графики, диаграммы и т.п.). Однако последние являются вспомогательными; основу же модели, доказательства её адекватности составляют те или иные направления аналитических и статистических представлений. Поэтому, несмотря на то, что по основным направлениям этих двух классов методов в вузах читаются самостоятельные курсы лекций, мы всё же кратко охарактеризуем их особенности, достоинства и недостатки с точки зрения возможности использования при моделировании систем.
Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек (безразмерных в строгих математических доказательствах), совершающих какие-либо перемещения в пространстве или взаимодействующих между собой.
Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.).
Аналитические представления имеют многовековую историю развития, и для них характерно не только стремление к строгости терминологии, но и к закреплению за некоторыми специальными величинами определённых букв (например, удвоенное отношение площади круга к площади вписанного в него квадрата π ≈ 3,14; основание натурального логарифма – е ≈ 2,7 и т.д.).
На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной науки – исследования операции, системный анализ, как математическое программирование (линейное, нелинейное, динамическое и т.п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.п.).
Эти теоретические направления стали основой многих прикладных, в том числе теории автоматического управления, теории оптимальных решений и т.д.
При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы, и их в этих случаях, вообще говоря, нельзя считать строгими математическими моделями.
Большинство из направлений математики не содержат средств постановки задачи и доказательства адекватности модели. Последняя доказывается экспериментом, который по мере усложнения проблем становится также всё более сложным, дорогостоящим, не всегда бесспорен и реализуем.
В то же время в состав этого класса методов входит относительно новое направление математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности моделей (стохастическое, нечеткое программирование).
Статистические представления сформировались как самостоятельное научное направление в середине прошлого века (хотя возникли значительно раньше). Основу их составляет отображение явлений и процессов с помощью случайных (стохастических) событий и их поведений, которые описываются соответствующими вероятностными (статистическими) характеристиками и статистическими закономерностями.
Статистические отображения системы в общем случае (по аналогии с аналитическими) можно представить как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (её учитываемые в модели свойства) оператор Ф[Sx]. «Размытую» точку следует понимать как некоторую область, характеризующую движение системы (её поведение); при этом границы области заданы с некоторой вероятностью p («размыты») и движение точки описывается некоторой случайной функцией.
Закрепляя все параметры этой области, кроме одного, можно получить срез по линии а–b, смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трёхмерную и т.д. картины статистического распределения.
Статистические закономерности можно представить в виде дискретных случайных величин и их вероятностей, или в виде непрерывных зависимостей распределения событий, процессов.
Для дискретных событий соотношение между возможными значениями случайной величины xi и их вероятностями pi, называют законом распределения и либо записывают в виде ряда (табл. 3.1), либо представляют в виде зависимостей F(x) (рис. 3.5, а) или p(х) (рис. 3.5, в).
Для непрерывных случайных величин (процессов) закон распределения представляют (соответственно дискретным законам) либо в виде функции распределения (интегральный закон распределения – рис. 3.5, б), либо в виде плотности вероятностей (дифференциальный закон распределения – рис. 3.5, г). В этом случае 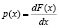
Для полной группы несовместных событий имеют место условия нормирования:
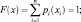
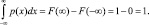
Часто применяют тот или иной вид зависимостей, приведенных на рис. 3.5, более подходящий для соответствующих приложений.
Источник
Способы моделирования системный анализ
При изучении систем различной природы исследователь сталкивается с проблемой их отображения, а также использования в познавательной и практической деятельности. Объект фиксируется терминами языка, отображается на бумаге чертежами, графиками, фотографиями, уравнениями и формулами, а также макетами, механизмами, устройствами. Потом эти отображения применяются для научного исследования (например, наблюдения, эксперимента) либо для практической деятельности. Отображения объектов называются моделями, процесс их создания — моделированием, а использование, соответственно, в науке называются модельным исследованием (модельным экспериментом, модельным наблюдением) и модельной практикой в практической деятельности. Способы построения моделей получили название методов моделирования. Они очень разнообразны. Практически каждая наука имеет свой арсенал методов моделирования. Различают геометрическое, физическое, химическое, биологическое, экономическое, социальное, политическое, культурологическое и математическое моделирование.
Понимание моделей в науке отличается известным разбросом. Наиболее краткое, почти афористичное ее определение дал А. И. Уемов, который считает, что модель представляет собой систему, исследование которой служит средством получения информации о другой системе [24, с. 48]. К. Б. Батароев дает развернутое определение модели: «Модель есть созданная или выбранная субъектом система, воспроизводящая существенные для данной цели познания стороны (элементы, свойства, отношения, параметры) изучаемого объекта и в силу этого находящаяся с ним в таком отношении замещения и сходства (в частности изоморфизма), что исследование ее служит опосредованным способом получения знания об этом объекте» [2, с. 28]. Необходимыми и достаточными признаками модели являются сформулированные В. А. Штоффом такие условия [27, с. 87-88]:
- между моделью и оригиналом имеется отношение сходства, форма которого явно выражена и точно зафиксирована (условия отражения или уточненной аналогии);
- модель в процессе научного познания является заместителем изучаемого объекта (условие репрезентации);
- изучение модели позволяет получить информацию (сведения) об оригинале (условия экстраполяции).
Заметим, что для метода моделирования свойственны некоторые парадоксы. Применение моделей обусловлено сложностью изучаемого объекта, поэтому модель проще оригинала. Она абстрагируется от несущественных качеств объекта. Однако в процессе исследования никогда нет 100 % уверенности в том, что то или иное качество объекта является несущественным с точки зрения исследовательской задачи. Поэтому простота модели может оказаться, что называется, «святой простотой».
Здесь же видится и другая особенность модели, которая роднит ее с одноразовой посудой. Каждая модель создается под определенную исследовательскую задачу и не применима к решению других, какой бы привлекательной модель ни была. Распространенный в науке перенос моделей с одной задачи на другую далеко не всегда оправдан и обоснован.
Классификация моделирования
Мир моделей разнообразен. Он обусловлен ростом многообразия и сложности человеческой деятельности. В. А. Штофф выделяет две большие группы моделей: материальные (менее удачные синонимы: вещественные, физические, действующие) и мысленные (менее удачные синонимы: идеальные, воображаемые, умозрительные). К числу материальных моделей относятся модели, которые сконструированы человеком искусственно или взяты из природы в качестве образцов. Мысленные же отличаются тем, что они созданы в форме мысленных образов, существующих лишь в голове исследователя, теоретика [27, с. 88-89].
Подобного же подхода придерживаются специалисты в области математики и кибернетики. Они делят моделирование на две большие разновидности: на физическое, при котором модель воспроизводит изучаемый процесс с сохранением изучаемых свойств, и математическое, при котором модель представляет собой математическое описание объекта моделирования.
К. Б. Батароев дает развернутую классификацию моделей, включая в нее: пространственно-геометрическое, физическое, химическое, математическое, кибернетическое, бионическое и биолого-информационное, экономико-математическое и социо-кибернетическое, эко-лого-кибернетическое, логическое, концептуальное, теоретическое, гносеологическое [2, с. 74-75].
Интересен подход к классификации моделей Ю. М. Плотинского, который выделяет среди разновидностей модели содержательную, формальную, концептуальную модели [20, с. 85-92]. То, что такие типы моделей существуют, ни у кого не может вызвать никаких сомнений. Другое дело, что эти модели из разных классов. Содержательная и формальная модели определяют отражение объекта, а концептуальная выделена по функциональному назначению.
По нашему мнению, известные классификации моделей и моделирования не всегда носят сущностный характер. Для того чтобы классификация отвечала природе моделей, она должна иметь три среза, которые соответствуют природе модели: отражательность, репрезентация и экстраполяция (табл. 22). Отражательный срез модели характеризуется ее субстанциональностью, т.е. той «материей», из которой «сотканы» объекты моделирования, их масштабами, временными характеристиками. Репрезентационный срез моделирования связан с целями исследования, формой модели, месте ее в познавательном процессе, связи с теми или иными методами науки и т.п. Экстраполяционный аспект модели заключается в использовании полученных посредством модели знаний, в распространении их на те или иные сферы деятельности человека.
| Основание классификации | Модель | |
|---|---|---|
| Вид | Характеристика | |
| Субстанциональный аспект модели | ||
| Природа объекта моделирования | Пространственно-геометрическая | Система, отражающая пространственное размещение объектов и процессов |
| Физическая | Система, отражающая совокупность физических объектов, действующих на физических законах | |
| Техническая | Система, отражающая техническое устройство | |
| Кибернетическая | Отражение кибернетической системы | |
| Химическая | Отражение химической системы | |
| Биологическая | Система, отражающая организмы или их сообщества | |
| Социальная | Модель общества или его составляющих | |
| Экономическая | Система, отражающая экономические объекты и процессы | |
| Политическая | Система, отражающая политические объекты и процессы | |
| Интеллектуальная | Система, отражающая знание, способы познания и мышления | |
| Масштабы объекта моделирования | Микромасштабная | Система, отражающая относительно небольшие образования |
| Макромасштабная | Система, отражающая значительные по величине образования | |
| Метамодель | Система, отражающая сверхбольшое образование | |
| Мегамодель | Система, отражающая бесконечное по величине образование | |
| Временная характеристика объекта моделирования | Историческая | Система, отражающая прошлое бытие объекта или процесса |
| Актуальная | Система, отражающая настоящее бытие объекта или процесса | |
| Прогностическая | Система, отражающая будущее бытие объекта и процесса | |
| Характер детерминации объекта моделирования | Стохастическая, вероятностная | Система, отражающая объект или процесс, поведение которого носит вероятностный характер |
| Детерминированная | Система, отражающая объект или процесс, поведение которого предопределено | |
| Динамика объекта | Статические | Отражает статические, неменяющиеся образования |
| Динамические | Отражает объекты, отличающиеся изменяемостью | |
| Репрезентационный аспект модели | ||
| Степень сложности модели | Простая | Система, состоящая из небольшого числа элементов и связей между ними |
| Сложная | Система, включающая в себя большое число простых моделей | |
| Сверхсложная | Система, включающая в себя большое число сложных моделей | |
| Способ отражения объекта | Содержательная | Отражает содержание системы |
| Формальная | Отражает объект на формальных языках | |
| Способ представления модели | Абстрактная | Единство некоторых символов или знаков |
| Материальная | Совокупность материальных явлений | |
| Форма представления модели | Графическая | Графики, диаграммы, блок-схемы и т. п. |
| Числовая | Конкретные числовые характеристики | |
| Логическая | Описывается в логических выражениях | |
| Математическая | Построена с использованием аппарата математики | |
| Мысленная | Выступает как некоторые идеи и представления об объекте | |
| Компьютерная | Реализуется с помощью компьютерной техники | |
| Материальная | Макеты, установки, тренажеры, действующие модели приборов и устройств | |
| Экстраполяционный аспект модели | ||
| Количество выполняемых моделью функций | Монофункциональная | Отличается одной узкой функцией |
| Полифункциональная | Отличается реализацией одновременно нескольких функций | |
| Характер выполняемых моделью функций | Исследовательская | Применяется в научном познании |
| Тренинговая | Используется для тренировки практических умений и навыков специалистов в различных областях | |
| Обучения | Для формирования у обучаемых знаний, умений и навыков | |
| Практическая | Заместители объектов в практической деятельности | |
| Роль в познании | Наблюдения | Используется для сбора фактов при наблюдении |
| Описательная | Дает описание объекта или процесса | |
| Экспериментальная | Для проведения эксперимента | |
| Концептуальная | Направлена на построение концепции того или иного объекта или процесса | |
| Теоретическая | Ориентирована на объяснение объекта или процесса посредством построения его теории | |
Таблица 22 — Классификация моделей
Сравнение классификаций систем и моделей приводит к выводу об их принципиальной схожести. Это обусловлено тем, что модель представляет собой специфическую разновидность системы, которая создается человеком специально для решения исследовательских задач. Поскольку системный метод выступает средством моделирования систем, то можно говорить о системном моделировании, предполагающем представление объектов любой природы в виде систем.
Системное моделирование включает две составляющие. Первая — это представление модели объекта или процесса как системы с ее основными параметрами и характеристиками. Модель здесь выступает совокупностью взаимосвязанных между собой элементов, отличается структурной организацией и функциональным предназначением. Вторая составляющая системного моделирования заключается в том, что системность состоит не только в качестве способа представления, но и в способе изучения модели. Известно, что моделирование — несамостоятельный способ научного познания, а создание для того или иного метода научного познания удобного для осуществления познавательных процедур объекта-модели. Отсюда вторая составляющая означает применение к системной модели системного анализа, который строится на знании системных закономерностей.
Особенности системного моделирования
Системное моделирование представляет собой совокупность конкретных разновидностей моделирования, наиболее важные среди которых:
- атрибутивное, направленное на систематизацию информации о свойствах объектов. При этом используются различного рода классификации, матрицы, таблицы, которые позволяют систематизировать свойства объектов, выделить главные и второстепенные;
- структурное, обеспечивающее представление структуры объекта или процесса моделирования;
- организационное, предполагающее изучение организации системы;
- функциональное, ориентированное на построение и исследование функций изучаемого явления;
- структурно-функциональное, ставящее своей целью исследование взаимосвязи структуры и функции изучаемого объекта или процесса;
- витальное, направленное на представление и изучение тех или иных этапов жизненного пути системы.
Системное моделирование не ограничивается удовлетворением простого любопытства по отношению к модели. Оно очень прагматично. Его важнейшим назначением выступает не просто получение знаний о системе, а ее оптимизация. Это поиск оптимума характеристик системы в соответствии с некоторыми критериями оптимальности. Математика оперирует понятием «оптимума функции». Оптимум функции f (x) на множестве M есть частное значение f (x0) этой функции, удовлетворяющее одному из соотношений: f (x0) больше и равно f (x) для всех х из М (глобальный максимум) или для всех f (x0) меньше и равно f (x) для всех х из М (глобальный минимум). Точка оптимума функции f (x) на множество M является одной из точек экстремума этой функции на множестве М.
Системное моделирование ориентировано на поиск в системной модели оптимальных характеристик в целях преобразования по принципам оптимальности реальных объектов практической деятельности людей.
Источник