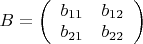Способы матричного представления графов

Матричное представление графов

Любой граф, заданный множествами Х и Г или в виде рисунка, может быть также представлен с помощью матриц смежности и инцидентности.

В квадратной матрице смежности строки и столбцы соответствуют вершинам графа. Для орграфа на пересечении i-той строки и j-того столбца матрицы значения элементов образуются по правилу

Для графа на рисунке 2.2 матрица смежности имеет вид:

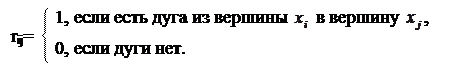Единицы в главной диагонали матрицы свидетельствуют о наличии петель в графе.

Для неорграфа в матрице смежности на пересечении строк и столбцов стоят единицы, если вершины соединены ребрами. Матрица, построенная по этому правилу для графа на рисунке 2.3 имеет вид

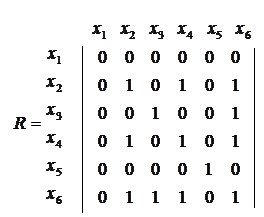или соответствует ранее построенной матрице отношений в примере 1.16. Поскольку отношения в неорграфе обладают свойством симметрии . Следовательно, все ребра определяются верхним правым треугольником матрицы, включающим диагональ. Поэтому для задания неорграфа можно использовать треугольную матрицу.

Существуют разновидности матриц смежности. В матрице весовых соотношений элемент вместо 1 принимает значения веса связи , в матрице длин – длины ребра или дуги .

В прямоугольной матрице инцидентности строки соответствуют вершинам графа, а столбцы – ребрам (дугам). Для неорграфа на пересечении i-той строки и j-того столбца элементы матрицы образуются по следующему правилу

Для графа, изображенного на рисунке 2.1в, матрица инцидентности имеет вид

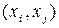
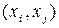
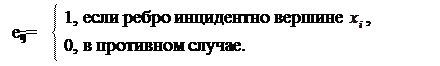
В каждом столбце матрицы Е не более двух единиц, поскольку каждое ребро соединяет две вершины. Столбцы, соответствующие петлям, содержат по одной единице.

Для орграфа в матрицу инцидентности заносится

Для графа на рисунке 2.2 матрица инцидентности записывается в виде:

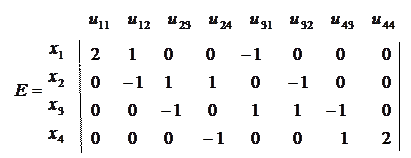
Матрица инцидентности, как и матрица смежности, однозначно определяет граф. Существуют приемы перехода от одной матрицы к другой.

С помощью матриц смежности можно установить изоморфизм графов. Для этого необходимо в матрице смежности одного графа проделать перестановки строк и столбцов. Если после очередной перестановки получим матрицу, тождественно совпадающую с матрицей другого графа, то графы изоморфны.

Помимо рассмотренных матриц, для описания графов используются матрицы контуров, расстояний и другие.

Контрольные вопросы

1) Из каких элементов состоит граф?

2) Какие различия имеются между ориентированным и неориентированным графами?

3) Как формируются матрицы смежности ориентированных и неориентированных графов?

4) Как формируются матрицы инцидентности ориентированных и неориентированных графов?

Дата добавления: 2014-12-27 ; просмотров: 3702 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

savastenko / 12. Способы матричного представления графов, их сравнение

12. Способы матричного представления графов, их сравнение.

Граф описывается перечислением множества вершин и дуг. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i,

Матричное представление графов

Графы удобно представлять в виде матриц смежности.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа ), однозначно представляющая его структуру.

A = ij>, i, j = 1, 2, . n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, если дуга (х_i, х_j),

Сравнение матриц графов.

Матрицы графов сравниваются для того чтобы выявить визуально незаметное сходство структуры графов.

Для сравнения графов используют их матричное представление. Из одной матрицы вычитается другая. Чем меньше полученный результат, тем более похожи графы.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Инцидентность и смежность в графах, матрицы смежности, матрицы инцидентности, списки инцидентности

Инцидентность вершин и рёбер графа, смежность вершин графа

Инцидентность — это когда вершина a является либо началом либо концом ребра e. Две вершины называются инцидентными, если у них есть общее ребро.

Для того, чтобы задать граф аналитически, множества V вершин графа и множества U рёбер графа, которые фигурировали в определении графа, будет недостаточно. Потребуется ещё и множество P троек вида (a, u, b) , указывающих какую пару a, b элементов множества вершин V соединяет тот или иной элемент u множества рёбер U графа. Элементы множества P называются инциденциями графа. Вот мы и подошли к одному из первых понятий теории графов — инцидентности.

Понятие инцидентности — одно из главных при создании структур данных для представления графов в памяти ЭВМ, к которым мы перейдём после примера 1.

Пример 1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)

Решение. Распространённые ошибки — не заметить вершины графа, которые не соединены ни с одной другой вершиной, в том числе с самой собой, и не включить их во множество вершин графа, а также указать не все рёбра графа, соединяющие две вершины. Поэтому вершину f данного графа обязательно включаем во множество вершин графа V , а, рёбра 6 и 7, хотя они соединяют одну и ту же вершину саму с собой и обе не имеют направления, включаем во множество рёбер U .

Итак, задаём граф следующими множествами:

множество рёбер: U =

Смежность вершин графа — это когда две вершины графа соединены ребром.

Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте. При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.

В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.

Наиболее часто используются три такие структуры данных — матрица смежности, матрица инцидентности и список инцидентности.

Матрицы смежности

Матрица смежности, как и матрица инцидентности, позволяет установить множество вершин, соседних с заданной (то есть рассматриваемой в конкретной задаче), не прибегая к полному просмотру всей матрицы. Матрицы смежности обычно представляются двумерным массивом размера n x n , где n — число вершин графа.

Матрица смежности S — это квадратная матрица, в которой и число строк, и число столбцов равно n — числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.

Матрица смежности для неориентированного графа

Элемент матрицы смежности s ij неориентированного графа определяется следующим образом:

— равен единице, если вершины v i и v j смежны;

— равен нулю, если вершины v i и v j не смежны.

Если для элемента матрицы v ij имеет место i = j , то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.

V	1	2	3	4	5
1	0	1	1	0	0
2	1	0	0	1	1
3	1	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.

Матрица смежности для ориентированного графа

Элемент матрицы смежности s ij ориентированного графа определяется следующим образом:

— равен единице, если из вершины v i в вершину v j входит дуга;

— равен нулю, если из вершины v i в вершину v j дуга не входит.

Как и для неориентированных графов, так и для ориентированных, если для элемента матрицы v ij имеет место i = j , то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 3. Составить матрицу смежности для графа, представленного на рисунке ниже.

V	1	2	3	4	5
1	0	1	0	0	0
2	0	1	0	0	0
3	1	0	0	0	0
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности ориентированного графа не симметрична.

Матрица смежности для графа с кратными рёбрами

Если в графе есть вершины, соединённые между собой несколькими рёбрами, то элемент матрицы смежности s ij равен числу рёбер, соединяющих вершины v i и v j . Из этого следует, что если вершины v i и v j не соединены рёбрами, то элемент матрицы смежности s ij равен нулю.

Пример 4. Составить матрицу смежности для графа, представленного на рисунке ниже.

V	1	2	3	4	5
1	0	3	2	0	0
2	3	0	0	1	1
3	2	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Матрица смежности для взвешенного графа

В случае взвешенного графа элемент матрицы смежности s ij равен числу w, если существует ребро между вершинами v i и v j с весом w. Элемент s ij равен нулю, если рёбер между вершинами v i и v j не существует.

Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.

V	1	2	3	4	5
1	0	11	9	0	0
2	11	0	0	5	8
3	9	0	0	0	2
4	0	5	0	0	0
5	0	8	2	0	0

Матрицы инцидентности

Матрица инцидентности H — это матрица размера n x m , где n — число вершин графа, m — число рёбер графа. Обычно в матрице инцидентности строки соответствуют вершинам графа, а столбцы — рёбрам графа.

Матрица инцидентности для неориентированного графа

Элемент матрицы инцидентности для неориентированного графа h ij определяется следующим образом:

— равен единице, если вершина v i инцидентна ребру e j ;

— равен нулю, если вершина v i не инцидентна ребру e j .

Пример 6. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

V	1-2	1-3	2-4	2-5	3-5
1	1	1	0	0	0
2	1	0	1	1	0
3	0	1	0	0	1
4	0	0	1	0	0
5	0	0	0	1	1

Матрица инцидентности для ориентированного графа

Элемент матрицы инцидентности для ориентированного графа h ij определяется следующим образом:

— равен минус единице, если вершина v i является началом ребра e j ;

— равен единице, если вершина v i является концом ребра e j ;

— равен нулю, если вершина v i не инцидентна ребру e j .

Пример 7. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

V	1-2	1-3	2-4	2-5	3-5
1	1	-1	0	0	0
2	-1	0	-1	-1	0
3	0	1	0	0	-1
4	0	0	1	0	0
5	0	0	0	1	1

Списки инцидентности

Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.

Список инцидентности одной вершины графа включает номера вершин, смежных с ней.

Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.

Пример 8. Составить списки инцидентности для графа, представленного на рисунке ниже.

Преимущества и недостатки каждого способа

Матрицы смежности и инцидентности целесообразнее использовать когда:

• число вершин графа невелико;
• число рёбер графа относительно большое;
• в алгоритме часто требуется проверять, соединены ли между собой две вершины;
• в алгоритме используются фундаментальные понятия теории графов, например, связность графа.

Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.

Списки инцидентности целесообразнее использовать когда:

• число вершин графа велико;
• число рёбер графа относительно невелико;
• граф формируется по какой-либо модели;
• во время действия алгоритма часто требуется модифицировать граф;
• в алгоритме часто используются локальные свойства вершин, например, например, окрестности вершин.

На практике списки чаще используются в прикладных целях.

Источник