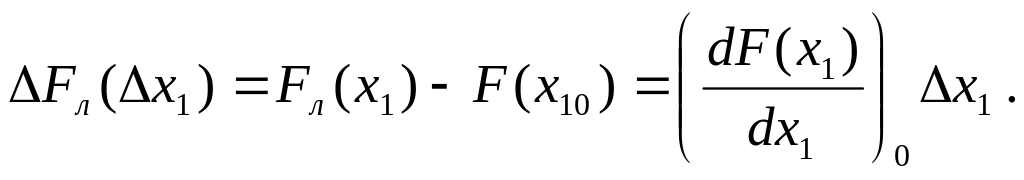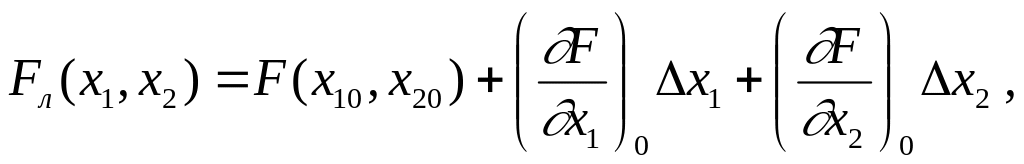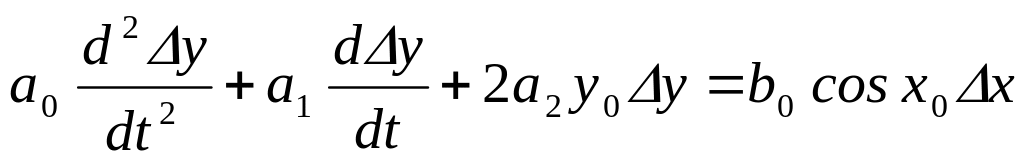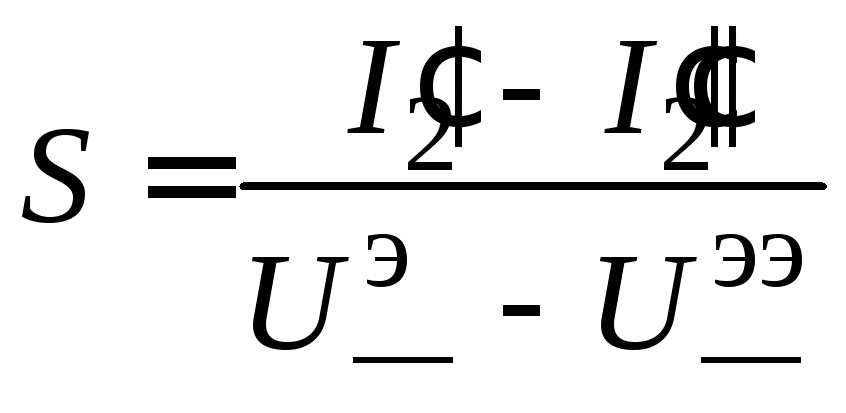Способы линеаризации нелинейных уравнений

Линеаризация нелинейных уравнений (Тема)

На практике все системы управления нелинейные, однако в некоторых случаях нелинейности настолько малы, что их эффект незначителен, или при больших нелинейностях система работает на линейных участках.

Процесс замены нелинейных уравнений близкими к ним по динамическим свойствам линейными уравнениями называется линеаризацией.

Существует несколько приёмов линеаризации. В данном подразделе рассматривается линеаризация, в основе которой лежит разложение нелинейностей в ряд Тейлора. Ниже дается упрощенная процедура линеаризации.

Пусть дана функция

. (1)

Предполагается, что система работает в режиме стабилизации, т.е.

. (2)

В идеальном установившемся режиме

. (3)

В действительности имеют место отклонения от точки (2), т.е.

. (4)

Предполагается что на порядок меньше .

Подставим (4) в (1). Тогда

. (5)

Последним слагаемым в (5) вследствие малости можно пренебречь.

Вычтем из (5) (3). Получим

. (6)

Уравнение (6) линейно относительно новых переменных .

Геометрический смысл линеаризации представлен на рисунке ниже.

Линеаризация путём разложения в ряд Тейлора представляет собой перенос начала координат из т. О в т. О ₁ и переход от переменных к новым переменным . В этом случае нелинейная функция АВ заменяется на касательную, проведенную в точке О₁.

Источник

§ 12. Линеаризация нелинейных функций и уравнений.

Линеаризация — приближённая замена нелинейной функции (уравнения) соответствующей линейной функцией (уравнением). Она производится в целях упрощения расчёта, но в ущерб точности.

Если исходное уравнение нелинейно, то из него необходимо выписать и линеаризовать все входящие в него нелинейные функции переменных (входных и выходных). Для линеаризации нелинейную функцию разла­гают в степенной ряд Тейлора в окрестности расчётного статического ре­жима и затем отбрасывают нелинейный остаток этого ряда в виду его малости.

Пусть имеется нелинейная функция F(x₁). Разложение в степенной ряд Тейлора выглядит следующим образом:

F(x₁₀) — значение в установившемся режиме. Первые два слагаемых образуют линейную часть ряда, а все остальные — нелинейный остаток (в общем случае он бесконечен). Обозначим x₁—x₁₀=Δx₁ — малое отклонение (приращение) x₁. Можно утверждать, что только при малости отклонений нелинейный остаток может быть отброшен, поскольку (Δx₁) 2 , (Δx₁) 3 — являются малыми величинами более высокого порядка малости, чем Δx₁. Это условие имеет под собой физическое обоснование: при высоком качестве регулирования величины отклоняются мало от своих постоянных значений. Второе условие линеаризации — дифференцируемость функции в рассматриваемой точке, т.е.

Линеаризованная функция равна линейной части ряда Тейлора:

(1)

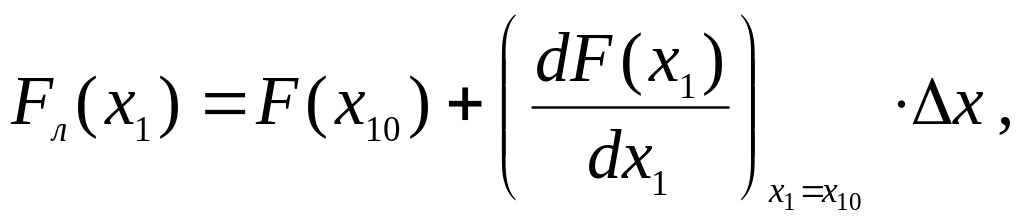
Отсюда можно найти линейное приращение нелинейной функции

Если нелинейная функция задана графически, то ее линеаризация производится по методу касательной, при этом небольшой отрезок этой функции

приближенно заменяется соответствующим отрезком касательной, угловой коэффициент которой находится из графика по формуле:

где m_F и m_x – масштабы по осям.

Если нелинейная функция зависит от нескольких переменных, то ее линеаризуют аналогично:

Линеаризация дифференциального уравнения может быть сведена к следующим преобразованиям: в нелинейном уравнении все входящие в него функции (как линейные так и нелинейные) заменяются своими линейными приращениями, производные от переменных по времени заменяются соответствующими производными от их приращений в силу того, что

, т.к. x₀=const

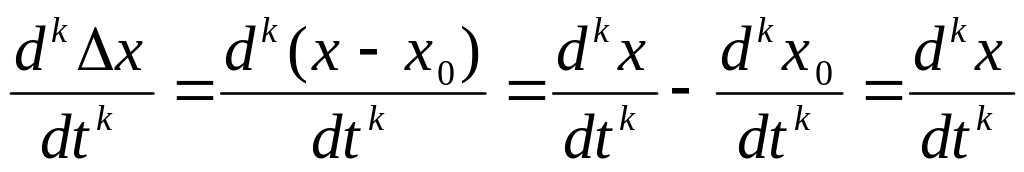
Приращение линейной функции получается при этом заменой переменной на ее приращение.

Пример:

Из уравнения статики a₂y 2 =b₀sin x найдем y₀, зная x₀. Затем получаем следующее линеаризованное уравнение для малых приращений:

Полученное таким образом линеаризованное уравнение приводится известным способом к стандартному виду, и по нему находятся передаточные функции для малых приращений.

§13. Cтруктурные схемы сар и их преобразования

Структурной называется схема, отражающая математическое преобразование сигналов. Она является по сути графической иллюстрацией к уравнениям системы.

Структурные схемы составляются для статических и динамических режимов и содержат следующие обозначения:

Звено обозначается прямоугольником, в котором записана математическая модель звена, например, в виде передаточной функции;

С

Входные и выходные величины — в виде стрелок.

Источник

2.2. Линеаризация нелинейных уравнений

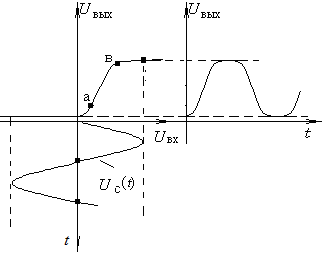
Рис. 2.3. Искажения выходного сигнала, вызванные нелинейностью характеристики «вход-выход» усилителя

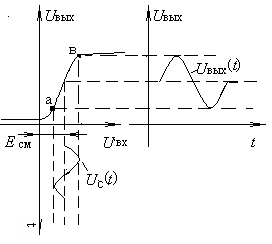
На практике встречается широкий класс задач, когда нелинейность электронного элемента (устройства) не является принципиально необходимой и даже, более того, может оказаться вредной. Так нелинейность характеристики «вход-выход» усилителя приводит к искажению формы усиливаемого сигнала (нелинейные искажения), который может оказаться неприемлемым, например, для качественно воспроизводимой музыки (рис. 2.3).

Ситуация изменится, если входной сигнал подать на вход усилителя на фоне постоянного пьедестала – напряжения смещения Е_см (см. рис. 2.4) так, чтобы размах сигнала не выходил за пределы практически линейного участка а–в.

Из рис. 2.4 видно, что, несмотря на сохранившуюся нелинейность характеристики усилителя, переменная составляющая выходного напряжения теперь линейно связана со входным сигналом U_вых(t) = kU_c(t).

В принципе, для любого нелинейного элемента с характеристикой «вход-выход»

для малых приращений относительно некоторого начального значения функции y₀ = F(x₀)

связь «вход=выход» может быть заменена линейной (рис. 2.5) связью для приращения

Рис. 2.5. Замена нелинейной зависимости y = F(x) линейной для малых приращений y = kx относительно исходного значения y₀, x₀

Рис. 2.4. Подача входного сигнала на постоянном пьедестале – напряжении смещения

Хотя уравнение (2.3) выглядит как линейное, оно называется линеаризованным, т. к. коэффициент уравнения k не является постоянной величиной, а зависит от начального значения y₀ функции:

Замена нелинейной связи y = F(x) линейной для приращений

относительно некоторого исходного значения функции y₀=F(x₀) называется линеаризацией  . Значения y₀, x₀, определяемые вектором «рабочей точки» по характеристике нелинейного элемента при x0, будем именовать режимом покоя нелинейного элемента (или начальным режимом при x = 0). Поскольку коэффициенты линеаризованного уравнения (в т. ч. и дифференциального), а следовательно и параметры устройства зависят от режима покоя, – это понятие очень важно для электроники, а оптимальный выбор режима покоя является достаточно сложной оптимизационной многопараметровой задачей, поскольку характер зависимости отдельных параметров элемента от режима покоя может быть диаметрально противоположным.

Математически переход от нелинейного уравнения к линеаризованному осуществляется путем разложения нелинейной функции в ряд Тейлора в окрестности режима покоя с удержанием в этом разложении только приращения первого порядка.

Для электронного двухполюсника, описываемого на постоянном токе нелинейным уравнением

линеаризованное уравнение примет вид

. (2.5)

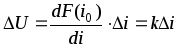
Очевидно, что коэффициент k уравнения (2.5) имеет размерность сопротивления, которое принято называть дифференциальным сопротивлением, или сопротивлением для приращений:

Переход от нелинейного уравнения (2.4) к линеаризованному (2.6) позволяет при анализе цепи для приращений заменить нелинейный двухполюсный элемент резистором, сопротивление r которого должно быть определено из статического режима.

Рассмотрим пример использования линеаризации для решения конкретной задачи.

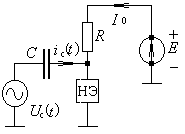
Рис. 2.6. Нелинейная цепь

На рис. 2.6 изображена схема, содержащая нелинейный элемент НЭ с характеристикой

В схеме действуют два источника – постоянная ЭДС Е и переменный сигнал U_c(t) произвольной формы. Необходимо определить значение тока i_c(t), потребляемого от источника переменного сигнала.

Допустим, что графоаналитическим методом определено значение постоянного тока I 0 .

Линеаризованное уравнение нелинейного элемента

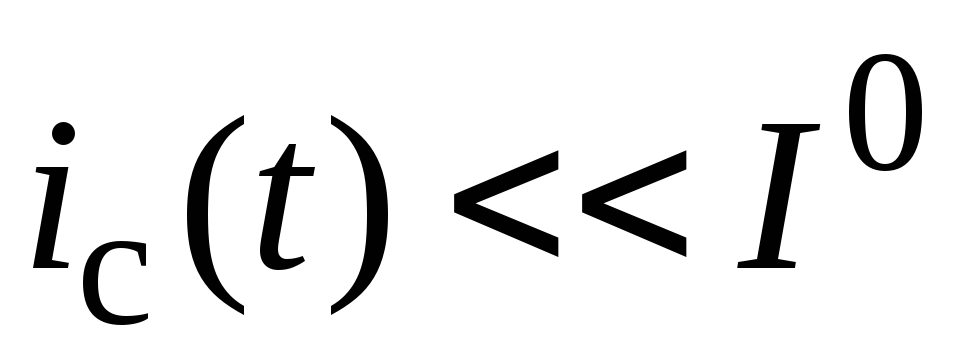
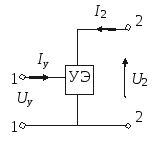
Полагая, что , заменим нелинейную цепь линеаризованной моделью (рис. 2.7). Теперь анализ такой цепи являетсядостаточно простой задачей. Особенностью линеаризованных моделей цепей является то, что постоянные источники в них отсутствуют, т. к. их приращения равны нулю (источник постоянной ЭДС заменяется закороткой, источник постоянного тока – разрывом).

Рассмотрим алгоритм линеаризации некоторого абстрактного управляющего элемента (рис. 2.8).

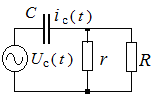
Рис. 2.7. Линеаризованная модель Рис. 2.8. Схема нелинейного

цепи по рис. 2.6 управляемого элемента

Пусть есть нелинейные зависимости

Проведем линеаризацию относительно режима покоя

Разложив зависимость (2.7) в ряд Тейлора, получим

(2.8)

=r₁₁.

Рис. 2.9. Линеаризованная электрическая модель управляемого элемента

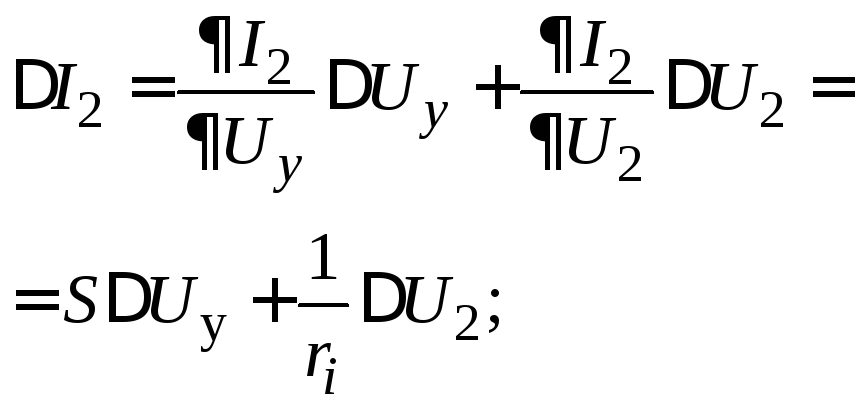
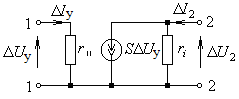
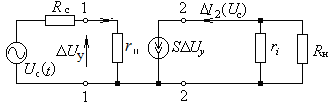
Оставляя пока без комментариев физический смысл коэффициентов линеаризованных уравнений S, r_i, r₁₁ на основании (2.8), можно построить электрическую линеаризованную модель управляемого элемента (рис. 2.9).

Рассмотрим пример использования линеаризованной модели для анализа усилительного устройства, изображенного на рис. 2.10.

Рис. 2.10. Схема усилительного устройства

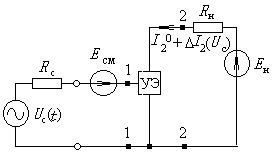
За счет источника смещения Е_см через управляемый элемент задается ток покоя I₂ 0 , а под воздействием сигнала U_c(t) этот ток получает полезное приращение I₂(U_c), которое и требуется определить.

Заменим схему нелинейного устройства на рис. 2.10 линеаризованной моделью этого устройства, для чего управляемый элемент заменим линеаризованной моделью, а источники постоянной ЭДС Е_см и Е_н закоротим (рис. 2.11). Ясно, что задача определения I₂(U_c) по такой схеме решается обычным методом электротехники.

Поскольку нелинейные зависимости (2.7) для конкретных управляемых элементов чаще всего задаются в виде статических (для постоянного тока) вольтамперных характеристик, то коэффициенты линеаризованного уравнения могут быть найдены графически. Допустим, что для некоторого элемента зависимость

задана графически (рис. 2.12).

Из уравнения (2.8) следует, например, что параметр

Рис. 2.11. Линеаризованная модель усилительного устройства

.

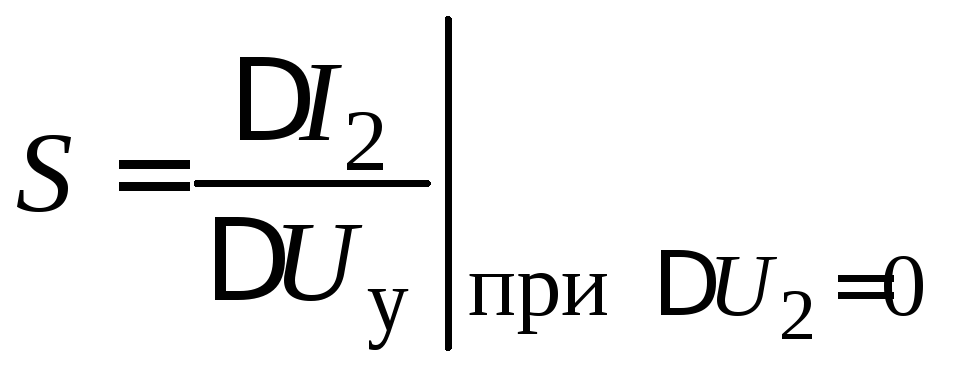
Условие U₂=0 означает, что приращения определяют при неизменном значении U₂ 0 , определяющем режим покоя.

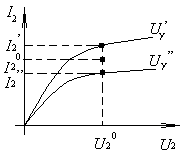
Рис. 2.12. Графическое определение коэффициента линеаризованного уравнения

Из рис. 2.12 очевиден алгоритм определения S. Аналогично можно определить и другие параметры линеаризованной модели, используя их определения из (2.8) и соответствующие вольт-амперные характеристики.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник