Тема 11. Нелинейные регрессии и их линеаризация
Аннотация.Данная тема раскрывает особенности построения нелинейных моделей регрессии.
Ключевые слова.Нелинейная регрессия, индекс корреляции, коэффициент эластичности, подход Бокса-Кокса.
Методические рекомендации по изучению темы
· Тема содержит лекционную часть, где даются общие представления по теме.
· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.
· Для проверки усвоения темы имеется тест для самоконтроля.
· Для подготовки к экзамену имеется контрольный тест.
Рекомендуемые информационные ресурсы:
2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. — 3-e изд., испр. и доп. — М.: ИНФРА-М, 2014. — 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 41-45.
3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 564 с.
(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 383-399.
4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. — М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. — 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.172-174.
Глоссарий
Бокса-Кокса подход – способ подбора линеаризующего преобразования.
Индекс корреляции—показатель корреляции, который определяется для нелинейных регрессий.
Коэффициент эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 процент.
Линеаризация нелинейных моделей – процедура, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований.
Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду.
Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции.
Вопросы для изучения
1. Классы и виды нелинейных регрессий.
2. Линеаризация нелинейных моделей. Выбор формы модели.
3. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).
Классы и виды нелинейных регрессий. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных; регрессии, нелинейные по оцениваемым параметрам. Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду. Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции. При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации.
Линеаризация нелинейных моделей. Выбор формы модели. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.
Рис. 11.1. Способы линеаризации
Замена переменных заключается в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Логарифмирование обеих частей уравнения применяется обычно, когда мультипликативную модель необходимо привести к линейному виду. К классу степенных функций относятся: кривые спроса и предложения, производственная функция Кобба-Дугласа, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий, зависимость валового национального дохода от уровня занятости.
Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса). Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
Здесь 
— общая дисперсия результативного признака y, 
— остаточная дисперсия, определяемая по уравнению нелинейной регрессии 
. По-другому можно записать так:
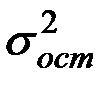
Следует обратить внимание на то, что разности в соответствующих суммах 
и 
берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Величина R находится в границах 
, и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Если разные модели используют разные функциональные формы для зависимой переменной, то проблема выбора модели становится более сложной, так как нельзя непосредственно сравнивать коэффициенты R 2 или суммы квадратов отклонений. Например, нельзя сравнивать эти статистики для линейного и логарифмического вариантов. Пусть в линейной модели в качестве зависимой переменной используется заработок, а в нелинейной – логарифм заработка. Тогда R 2 в одном уравнении измеряет объясненную регрессией долю дисперсии заработка, а в другом — объясненную регрессией долю дисперсии логарифма заработка. В случае, если значения R 2 для двух моделей близки друг к другу, проблема выбора усложняется. Здесь следует использовать тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и lny проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать суммы квадратов отклонений в линейной и логарифмической моделях. Здесь выполняются следующие шаги. Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y. Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*. Оцениваются две регрессии: для линейной модели с использованием y* в качестве зависимой переменной и для логарифмической модели с использованием ln y* вместо ln y. Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным. Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz, где z – отношение значений остаточной СКО в перечисленных регрессиях. Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания.
Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %:
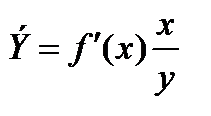
В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:
| Вид уравнения регрессии | Коэффициент эластичности |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
  |  |
 |
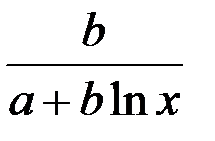Вопросы и задания для самоконтроля
1. Какие модели являются нелинейными относительно: а) включаемых переменных; б) оцениваемых параметров?
2. Какие преобразования используются для линеаризации нелинейных моделей?
3. Чем отличается применение МНК к моделям, нелинейным относительно включаемых переменных, от применения к моделям, нелинейным по оцениваемым параметрам?
4. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
5. Какие показатели корреляции используются при нелинейных соотношениях рассматриваемых признаков?
6. В каких случаях используют обратные и степенные модели?
Задача 1.По группе предприятий, производящих однородную продукцию известно, как зависит себестоимость единицы продукции (Y) от факторов, приведенных в таблице:
| Признак-фактор | Уравнение парной регрессии | Среднее значение фактора |
Объем производства,  млн. руб. |  |  |
Трудоемкость единицы продукции,  чел/час |  |  |
Оптовая цена за 1т энергоносителя,  , млн. руб. |  |  |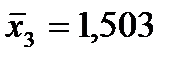
Доля прибыли, изымаемая государством,  ,% |  |  |
1) определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;
2) ранжировать факторы по силе влияния на результат.
Задача 2. По группе из 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции 
(тыс. руб) от уровня технической оснащенности 
(тыс. руб.)
.
Доля остаточной дисперсии в общей составила 0,19.
1) определить коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.;
2) вычислить индекс корреляции;
3) оценить значимость уравнения регрессии с помощью 
критерия.
Источник
Тема 4. Нелинейные модели регрессии и их линеаризация
Довольно часто соотношения между социально-экономическими явлениями и процессами приходится описывать нелинейными функциями. Например, производственные функции (зависимость между объемом производства и основными факторами производства) или функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом).
Следует различать модели, нелинейные по параметрам, и модели, нелинейные по переменным.
Для оценки параметров нелинейных моделей существует два основных подхода:
1. Первый подход основан на линеаризации модели: преобразованием исходных переменных и введением новых, нелинейную модель можно свести к линейной, для оценки параметров которой используется метод наименьших квадратов.
2. Если подобрать соответствующее линеаризующее преобразование не удается, то применяются методы нелинейной оптимизации на основе исходных переменных.
Если модель нелинейна по переменным, то используется первый подход, т.е. вводятся новые переменные, и модель сводится к линейной:
y =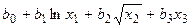 
+ ε.
Переходим к новым переменным: x1‘=lnx1, x2‘=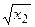 
и получаем линейное уравнение:
y =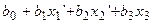 
+ ε.
Более сложной проблемой является нелинейность по оцениваемым параметрам. В ряде случаев путем подходящих преобразований эти модели удается привести к линейному виду. Рассмотрим следующие модели, нелинейные по оцениваемым параметрам:
· степенная (мультипликативная) –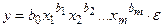 
,
Степенная модель может быть преобразована к линейной путем логарифмирования обеих частей уравнения:
lny = ln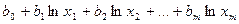 
+ lnε.
y‘ =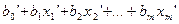 
+ ε‘.
Степенные модели получили широкое распространение в эконометрическом моделировании ввиду простой интерпретации параметров, которые представляют собой частные коэффициенты эластичности результативного признака по соответствующим факторным признакам.
· экспонента –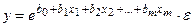 
,
Экспоненциальная модель линеаризуется аналогично:
lny =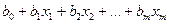 
+ lnε.
Переходя к новым переменным y’=lny, ε‘=lnε, получаем линейную регрессионную модель:
y‘ = 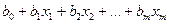+ ε‘.
· гипербола –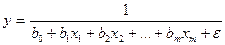 
.
Гиперболическая модель линеаризуется непосредственной заменой переменной y‘=1/y:
y‘ = 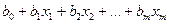+ ε.
Эти функции используются при построении кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей или от цены товара.
y = 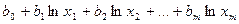+ ε.
При выборе формы уравнения регрессии важно помнить, что чем сложнее функция, тем менее интерпретируемы ее параметры.
В качестве примера использования линеаризующего преобразования регрессии рассмотрим производственную функцию Кобба-Дугласа:
где Y – объем производства, К – затраты капитала, L – затраты труда.
Путем логарифмирования обеих частей данную степенную модель можно свести к линейной:
Переходя к новым переменным Y‘=lnY, A‘=lnA, K‘=lnK, L‘=lnL, ε‘=lnε, получаем линейную регрессионную модель:
Эластичность выпуска продукции.
Показатели α и β являются коэффициентами частной эластичности объема про-изводства Y соответственно по затратам капитала К и труда L. Это означает, что с увели-чением только затрат капитала (труда) на 1% объем производства возрастает на α% (β%):
;
.
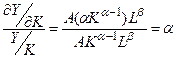
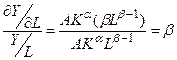
Эффект от масштаба производства.
Если α и β в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то Y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства. Если их сумма меньше единицы, то имеет место убывающий эффект от масштаба производства. Например, К и L увеличиваются в 2 раза. Найдем новый уровень выпуска (Y*):
Y* = A(2K) α (2L) β = A2 α K α 2 β L β = 2 α + β AK α L β = 2 α + β Y.
Если α+β =1,2, то 2 α + β =2,30, а Y увеличивается больше, чем в 2 раза.
Если α+β =1, то 2 α + β =2, и Y увеличивается также в 2 раза.
Если α+β =0,8, то 2 α + β =1,74, а Y увеличивается меньше, чем в 2 раза.
Первоначально Кобб и Дуглас представляли функцию в виде Y = AK α L 1- α ε,
т.е. предполагали постоянную отдачу от масштаба производства. Впоследствии это допущение было ослаблено.
Если в модели α+β =1, то функцию Кобба-Дугласа представляют в виде
Y = AK α L 1- α ε
или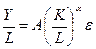 
.
Таким образом, переходят к зависимости производительности труда (Y/L) от его капиталовооруженности (К/L). Логарифмируя обе части уравнения, приводим его к линейному виду:
Функция Кобба-Дугласа с учетом технического прогресса имеет вид:
Y = AK α L β e θt ε,
где t – время, параметр θ – темп прироста объема производства благодаря техническому прогрессу.
Источник
