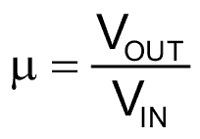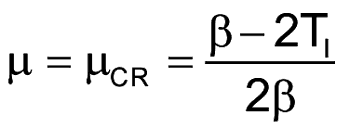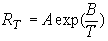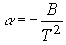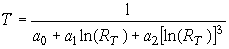Способы линеаризации характеристик термисторов

Новая формула для линеаризации характеристик термисторов

Довольно часто мне требуется с хорошей точностью измерить температуру лазера, транзистора или печатной платы. Обычно в качестве датчиков я использую для этого термисторы, поскольку они очень дешевы. Однако нелинейная характеристика сопротивления термистора затрудняет получение точных результатов. Чтобы сделать задачу менее трудоемкой, я часто линеаризую характеристику термистора, делая его элементом резистивного делителя напряжения. Отклик линеаризованного термистора намного проще преобразовать в температуру, чем напряжение, измеренное на одиночном термисторе. Для оптимизации параметров делителя я вывел пару формул, которыми пользуюсь для вычисления величин сопротивлений резисторов R_S и R_P, используемых в схеме линеаризации.

На Рисунке 1 показана схема линеаризации термистора, о которой я хочу рассказать ниже. Ее выходное напряжение приблизительно линейно зависит от температуры.

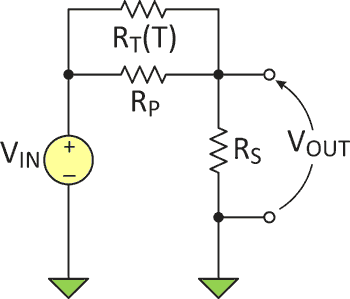Рисунок 1.	Линеаризация характеристики термистора с помощью двух резисторов.

Начнем с выбора температуры T_I, которую я называю «температурой перегиба», при которой мы хотим иметь наилучшее совпадение линеаризованной характеристики V_OUT/V_IN с идеальной. Конечной целью будет вычисление значений сопротивлений R_S и R_P и отношения

при температуре T_I.

Зависимость сопротивления термистора R_T от температуры T часто описывают следующим выражением

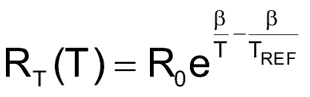(1)

R₀ – сопротивление термистора при опорной температуре T_REF,
β – коэффициент температурной чувствительности.

R_S и R_P я нашел, приравняв к нулю вторую производную от V_OUT/V_IN (Рисунок 1) при температуре T_I. После достаточно громоздких алгебраических преобразований я получил следующие формулы:

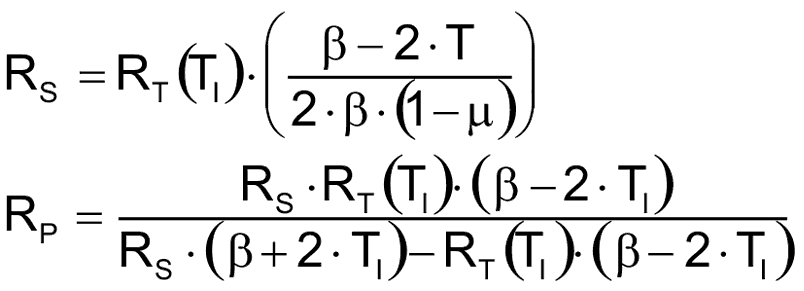(2)

Физическая реализация схемы линеаризации на пассивных компонентах возможна не при любых µ. При

значение R_P получается отрицательным.

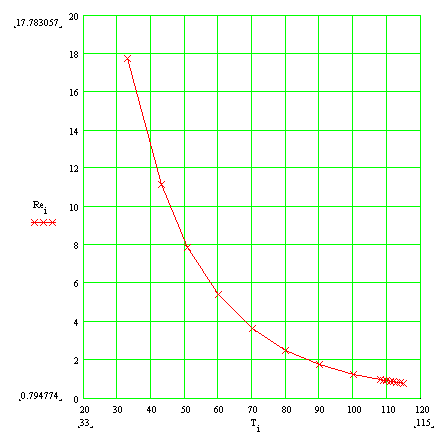
На Рисунке 2 показана передаточная функция обычного линеаризованного термистора.

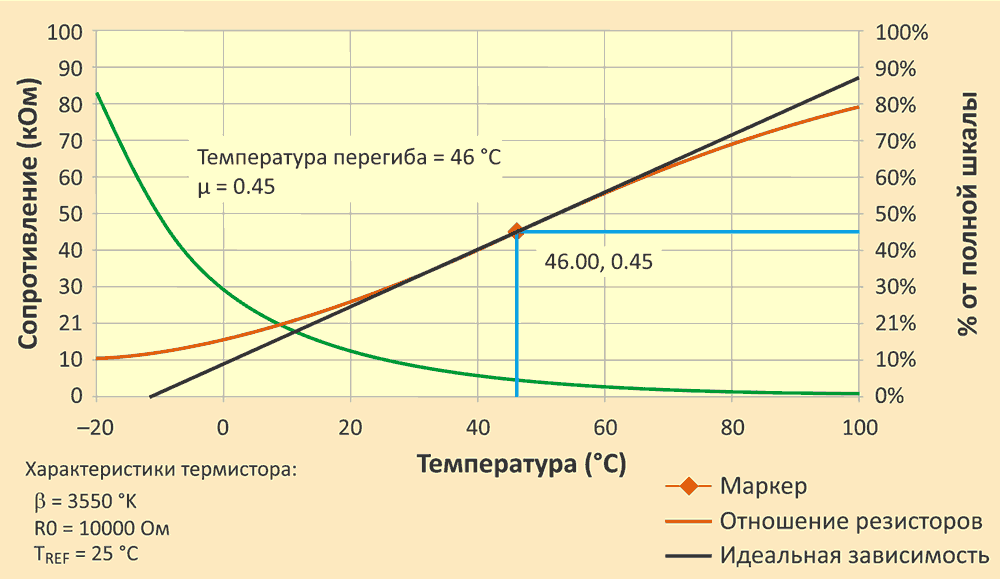Рисунок 2.	Сравнение передаточной функции линеаризованного термистора с идеальной.

Использованные при расчетах и моделировании рабочие таблицы Excel и файл Mathcad доступны для скачивания в разделе Загрузки.

Загрузки

Перевод: AlexAAN по заказу РадиоЛоцман

Источник

Применение терморезисторов (термисторов) для измерения температуры

Введение

Терморезисторы (термисторы) — это резисторы, сопротивление которых сильно изменяется в зависимости от температуры. Термисторы изготавливаются на основе полупроводникового материала и имеют нелинейную вольт-амперную характеристику. Термисторы с положительным температурным коэффициентов сопротивления (ТКС) называются позисторами. Благодаря чувствительности к температуре термисторы используются для измерения температуры и построения систем управления температурой в технологическом и лабораторном оборудовании.

Терморезисторы изготавливаются на основе полупроводникового оксида металлов, спрессованного для получения заданной формы. Механическая прочность и защита от воздействий окружающей среды обеспечивается с помощью металлического корпуса или защитного изолирующего слоя. Термисторы имеют нелинейную вольт-амперную характеристику и очень высокую температурную чувствительность по сравнению с другими типами датчиков температуры. Типовое значение ТКС для термисторов составляет -5% на градус, в то время как для платинового термопреобразователя (RTD) он составляет 0,4% на градус.

Типовой диапазон температур термисторов достаточно узок (-60. +150 С), для некоторых образцов он расширен до (-60. +300 С).

Важным преимуществом термисторов является их большое сопротивление, что устраняет проблему, связанную с падением напряжения на подводящих проводах, как при использовании RTD или проблему, связанную с необходимостью большого усиления сигнала (до 2000) для термопар.

Температурная зависимость

Зависимость сопротивления термисторов от температуры в диапазоне нескольких десятков градусов удовлетворительно описывается экспоненциальной функцией (рис.1)

где А — сопротивление при бесконечно большой температуре, В — коэффициент температурной чувствительности (его значения обычно лежат в диапазоне 1200-16000).

Из выражения (1) можно получить связь между ТКС терморезистора ( 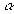) и коэффициентом температурной чувствительности в виде

Величину ТКС обычно приводят в справочниках для температуры 20 С (293 К).

Рис.1. Зависимость сопротивления от температуры для термистора ММТ-1 22Ком.

При протекании тока через терморезистор он нагревается, что увеличивает погрешность измерений. Поэтому при выборе терморезистора необходимо учитывать его коэффициент рассеяния, который определяется как мощность, приводящая к нагреву терморезистора на 1 градус относительно температуры окружающей среды. Для снижения погрешности, вызванной собственным разогревом термистора, необходимо увеличивать площадь его поверхности, однако это приводит к увеличению тепловой инерционности, которая характеризуется величиной постоянной времени. Постоянная времени терморезистора равна времени, в течение которого его температура изменяется в е раз (на 63%) при перенесении термистора из воздушной среды с температурой 0 град. Цельсия в воздушную среду с температурой 100 град. Типовые значения постоянных времени лежат в диапазоне от десятых долей секунды до нескольких минут.

Линеаризация характеристик

В связи с сильной нелинейностью температурной зависимости терморезисторы не могут быть использованы без компенсации нелинейности (линеаризации) их характеристики. Для этой цели используют нелинейные аппроксимирующие функции, коэффициенты которых подбирают методом наименьших квадратов или другими методами параметрической идентификации. Этот недостаток термисторов сильно ограничивал их применение до появления средств измерения температуры, построенных на базе компьютера. Применение компьютера позволяет легко скомпенсировать нелинейность программным путем. Эта особенность увеличила интерес к применению термисторов в последние годы и инициировала дальнейшие исследования в направлении улучшения их стабильности, точности и взаимозаменяемости.

Для компенсации нелинейности термисторов используют формулу Стейнхард-Харта:

где температура дана в градусах Кельвина, (К = С + 273,15); 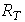— сопротивление термистора. Коэффициенты уравнения подбираются из условия наилучшего приближения к экспериментально полученной зависимости или поставляются изготовителем термистора.

Измерительная цепь

Цепь измерения температуры с использованием термистора состоит из источника тока и самого термистора. Падение напряжения на термисторе прямо пропорционально его сопротивлению и считывается дифференциальным усилителем. Для устранения паразитного влияния помех усилитель должен иметь достаточно большой коэффициент ослабления синфазного сигнала.

Несколько худший результат по температурной чувствительности дают измерительные схемы, в которых ток термистора задается не от идеального источника тока, а от источника напряжения через последовательно включенное сопротивление.

Чувствительность схемы измерения температуры пропорциональна величины тока через термистор. Поэтому этот ток следует выбирать как можно больше, но так, чтобы погрешность. вносимая эффектом саморазогрева термистора, находилась в допустимых пределах. Перегрев термистора на 1 градус вызывается мощностью, равной его коэффициенту рассеяния.

Коэффициент рассеяния существенно зависит от теплопроводности среды, в которой находится терморезистор (вода, воздух, контакт с металлом), поэтому необходимо принимать во внимания условия, при которых он измеряется изготовителем. При использовании термистора в иной среде необходимо предварительно измерять коэффициент рассеяния. Например, если на термисторе рассеивается мощность 2 мВт, а его коэффициент рассеяния равен 10 мВт/град, то саморазогрев термистора составит 0,2 град. Если требуемая погрешность измерения должна быть меньше, следует уменьшить ток через термистор и улучшить экранирование токоподводящих проводов, поскольку при уменьшении тока ухудшается отношение сигнал/помеха.

Для улучшения отношения сигнал/помеха при значительном удалении термодатчика от системы сбора данных используют фильтр нижних частот с полосой, которая зависит от требуемой скорости измерений и тепловой инерционности термодатчика. Типовым применениям удовлетворяет фильтр третьего порядка с полосой 5 Гц, например, фильтр RL-8F3 из серии RealLab!

Располагается на площади 6500 м², оснащено самым современным технологическим оборудованием, имеет научно-исследовательское и конструкторское подразделение, использующие передовые средства автоматизации проектирования.

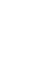Телефон:

Режим работы:
Адрес:

Почта:

© НИЛ АП, ООО, 1989-2021
© Microsoft, Windows, and the Windows CE are registered trademarks of Microsoft Corporation in the United States and/or other countries

Источник

Измерение температуры с помощью термистора NTC

Узнайте о термисторах и о том, как запрограммировать Arduino для измерения их данных.

Вы когда-нибудь задумывались над тем, как некоторые устройства, такие как термостаты, нагревательные площадки 3D принтеров, автомобильные двигатели и печи измеряют температуру? В этой статье вы можете это узнать!

Знать температуру может быть очень полезно. Знание температуры может помочь регулировать температуру в помещении до комфортного значения, гарантировать, что нагревательная площадка 3D принтера была достаточно горячей, чтобы такие материалы, как ABS, прилипали к ее поверхности, а также предотвратить перегрев двигателя или не допустить сжигания приготавливаемой еды.

В данной статье мы рассматриваем только один тип датчика, способного измерять температуру. Этот датчик называется термистором.

Термистор обладает сопротивлением, которое намного сильнее зависит от температуры, чем сопротивление других типов резисторов.

Мы буде использовать Arduino для измерения и обработки показаний термистора, после чего мы преобразуем эти показания в удобный для чтения формат единиц измерения температуры.

Ниже приведена фотография термистора, который мы собираемся использовать:

Терморезистор

Необходимые компоненты

Комплектующие

• Arduino (Mega или Uno или любая другая модель);
• несколько перемычек;
• паяльник и припой (возможно, понадобится, если ваш термистор не будет влезать в разъемы на плате Arduino).

Программное обеспечение

Теория

При типовом использовании резистора вы не хотите, чтобы его сопротивление менялось при изменении температуры. Это не реально в реальной жизни, можно лишь обеспечить небольшое изменение сопротивления при большом изменении температуры. Если бы это было не так, то резисторы странно влияли бы на работу схем, например, светодиод мог бы светиться намного ярче или тусклее по мере изменения температуры окружающей среды.

Но что, если вы действительно хотите, чтобы яркость светодиода была функцией температуры? Здесь появляется термистор. Как вы могли догадаться, у термистора сопротивление сильно изменяется при небольшом изменении температуры. Чтобы проиллюстрировать это, ниже приведена кривая изменения сопротивления термистора:

График зависимости сопротивления термистора от температуры

На рисунке показаны лишь единицы измерения без фактических значений, так как диапазон сопротивлений зависит от типа конкретного термистора. Как вы можете заметить, по мере увеличения температуры сопротивление терморезистора уменьшается. Это является отличительным свойством резистора с отрицательным температурным коэффициентом (Negative Temperature Coefficient), или, кратко, NTC термистора.

Существуют также терморезисторы с положительным температурным коэффициентом (Positive Temperature Coefficient, PTC), сопротивление которых увеличивается по мере роста температуры. Однако, PTC термисторы имеют своего рода точку перелома и сильно меняют сопротивление при некоторой температуре. Это делает взаимодействие с PTC термисторами чуть более сложным. По этой причине в большинстве дешевых измерителей температуры предпочтительнее использовать NTC термисторы.

В оставшейся части статьи, как вы можете догадаться, мы будем говорить о терморезисторах типа NTC.

Четыре подхода к нахождению формулы для построения кривой

Теперь, когда мы лучше понимаем поведение термисторов, вы можете удивиться, как мы можем использовать Arduino для измерения температуры. Кривая на графике выше нелинейна и, следовательно, простое линейное уравнение нам не подходит (на самом деле мы можем вывести уравнение, но об этом позже).

Так что же делать?

Прежде чем продолжить, подумайте, как бы вы это сделали на Arduino или даже в схеме без микропроцессорных компонентов.

Существует несколько способов решения этой проблемы, которые перечислены ниже. Это далеко не полный список всех методик, но он покажет вам некоторые популярные подходы.

Метод 1

Некоторые производители предоставляют настолько полную информацию, что в ней содержится весь график, отображающий определенные диапазоны целочисленных значений температуры и сопротивления (типовые значения). Один такой термистор может быть найден в техническом описании от компании Vishay.

Как, имея такие подробные данные, можно было бы реализовать измерение температуры на Arduino. Вам нужно было бы жестко прописать в коде все эти значения в огромной таблице поиска или очень длинных структурах управления » switch. case » или » if. else «.

А если производитель не удосужился предоставить подробную таблицу, то вам придется самостоятельно измерить каждую точку для формирования такой таблицы. Этот день будет для программиста довольно уныл. Но этот метод не так уж и плох и имеет место в использовании. Если текущий проект проверяет лишь несколько точе или даже небольшой диапазон, этот способ может быть предпочтительным. Например, одна такая ситуация возникает, если вы хотите измерить, находятся ли значения выбранных диапазонах температур, и зажечь светодиод для индикации этого состояния.

Но в нашем проекте мы хотим измерять температуру в почти непрерывном диапазоне и отправлять показания на монитор последовательного порта, поэтому этот метод использовать не будем.

Метод 2

Вы можете попытаться «линеаризовать» реакцию термистора, добавив к нему дополнительную схему.

Одним из популярных способов выполнения этого является подключение резистора параллельно термистору. Некоторые микросхемы предлагают сделать это за вас.

Определение того, как выбрать и линеаризовать участок кривой, вместе с выбором правильного номинала резистора – это тема для отдельной статьи. Этот подход хорош, если микропроцессор не может вычислять выражения с плавающей запятой (например, PICAXE), поскольку он упрощает реакцию в некотором диапазоне температур до линейного характера. Это также упрощает проектирование схемы, в которой нет микропроцессора.

Но у нас в этой статье микропроцессор используется, и мы хотим измерять температуру во всем диапазоне.

Метод 3

Вы можете взять данные из таблицы в техническом описании или (если нравятся извращения) сформировать собственную таблицу, выполнив самостоятельные измерения и воссоздав график в чем-то типа Excel. Затем вы можете использовать функцию подгонки кривой для создания формулы этой кривой. Это неплохая идея, и вся выполненная работа даст красивую формулу, которую вы сможете использовать в программе. Но это займет некоторое время для предварительной обработки данных.

Хотя это разумный подход, мы не хотим зависеть от анализа всех этих данных. Кроме того, каждый термистор немного отличается (но, конечно, это не проблема, если допуск довольно низок).

Метод 4

Оказывается, есть общая формула для подгонки кривой, предназначенная для устройств типа термисторов. Она называется уравнением Штейнхарта-Харта. Ниже представлена его версия (в других версиях используются члены во второй и степени):

где R – сопротивление терморезистора при температуре T (в Кельвинах).

Это общее уравнение кривой, подходящее для всех типов NTC термисторов. Аппроксимация связи температуры и сопротивления «достаточно подходит» для большинства применений.

Обратите внимание, что уравнение нуждается в константах A, B и C. Для разных термисторов они различаются и должны быть либо заданы, либо вычислены. Поскольку мы имеем три неизвестных, вам необходимо выполнить три измерения сопротивления при определенных температурах, которые затем могут быть использованы для создания трех уравнений и определения значений этих констант.

Даже для тех из нас, кто хорошо знают алгебру, это всё еще слишком трудоемко.

Вместо этого, есть еще более простое уравнение, которое менее точно, но содержит только одну константу. Эта константа обозначена как β, и поэтому уравнение называется β-уравнением.

где R₀ – сопротивление при контрольной температуре T₀ (например, сопротивление при комнатной температуре). R – сопротивление при температуре T. Температуры указываются в Кельвинах. β обычно указывается в техническом описании; а если нет, то вам необходимо только одно измерение (одно уравнение) для расчета этой константы. Это уравнение я буду использовать для взаимодействия с нашим термистором, поскольку оно является самым простым из тех, с которыми я столкнулся, и не нуждается в линеаризации реакции термистора.

Измерение сопротивления с помощью Arduino

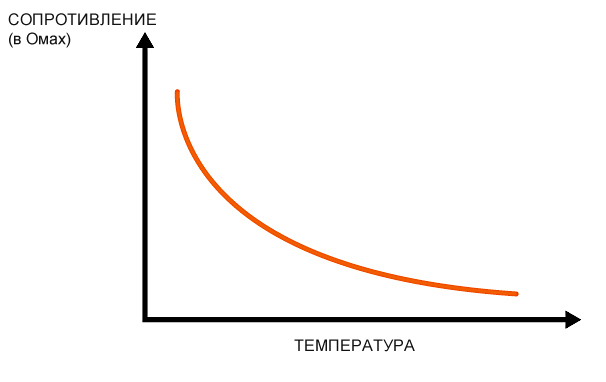
Теперь, когда мы выбрали метод построения кривой, мы должны выяснить, как реально измерить сопротивление с помощью Arduino, прежде чем мы сможем передать информацию о сопротивлении в β-уравнение. Мы можем сделать это используя делитель напряжения:

Делитель напряжения для измерения сопротивления термистора

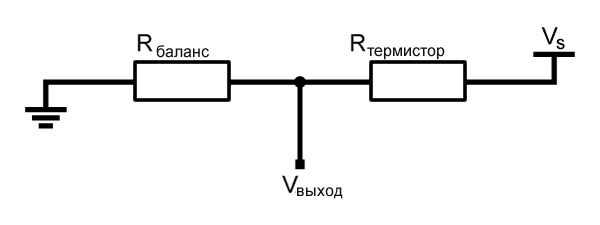
Это будет наша схема взаимодействия с термистором. Когда термистор определит изменение температуры, это отразится на выходном напряжении.

Теперь, как обычно, мы используем формулу для делителя напряжения.

Но нам неинтересно выходное напряжение V_выход, нас интересует сопротивление термистора R_{термистор}. Поэтому мы выразим его:

Это намного лучше, но нам необходимо измерить наше выходное напряжение, а также напряжение питания. Так как мы используем встроенный АЦП Arduino, то можем представить напряжение, как числовое значение на определенной шкале. Итак, конечный вид нашего уравнения показан ниже:

Это работает потому, что не имеет значения, как мы представляем напряжение (в вольтах или в цифровых единицах), эти единицы сокращаются в числителе и знаменателе дроби, оставляя безразмерное значение. Затем мы умножаем его на сопротивление, чтобы получить результат в омах.

D_max у нас будет равно 1023, так как это самое большое число, которое может выдать наш 10-разрядный АЦП. D_{измеренное} – это измеренное значение аналого-цифровым преобразователем, которое может быть в диапазоне от нуля до 1023.

Всё! Теперь можно приступить к сборке!

Соберем это

Я использовал термистор TH10K.

Также я использовал резистор 10 кОм в качестве R_баланс в нашем делителе напряжения. Константы β у меня не было, поэтому я рассчитал ее сам.

Ниже приведена полная схема устройства. Она довольно проста.

Схема измерения температуры с помощью Arduino и NTC термистора

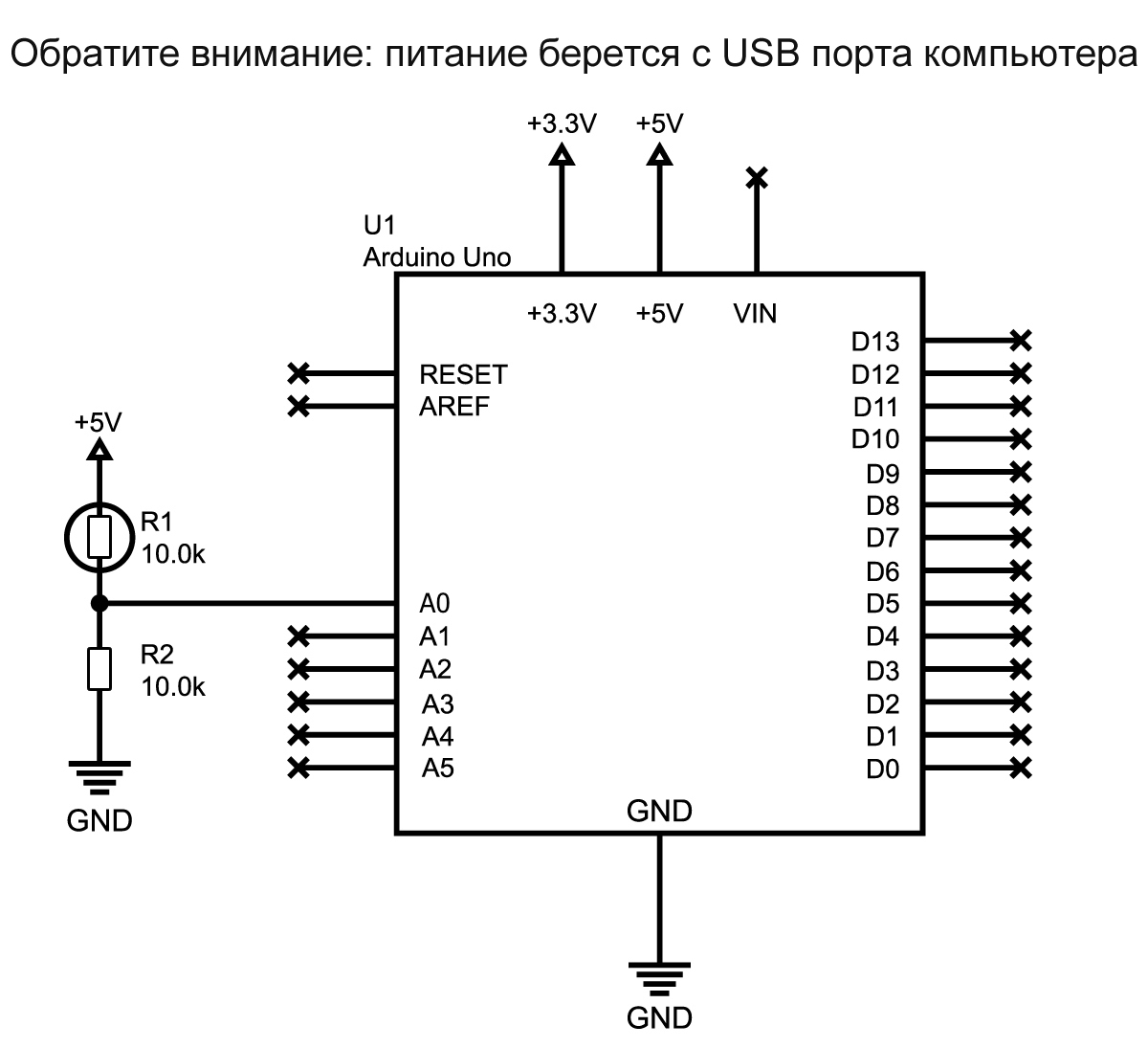
А так выглядит конечный макет:

Макет измерения температуры с помощью Arduino и NTC термистора

Код программы для Arduino

Код снабжен большим количеством комментариев, чтобы помочь вам понять логику программы.

В основном он измеряет напряжение на делителе, вычисляет температуру, а затем показывает ее в терминале последовательного порта.

Для забавы добавлены также некоторые операторы » if. else «, чтобы показать, как вы можете действовать в зависимости от диапазона температур.

Возможные следующие шаги

Всё в данной статье показывает довольно простой способ измерения температуры с помощью дешевого термистора. Есть еще пара способов улучшить схему:

• добавить небольшой конденсатор параллельно выходу делителя. Это стабилизирует напряжение и может даже устранить необходимость усреднения большого количества выборок (как было сделано в коде) – или, по крайней мере, мы сможете усреднять меньшее количество выборок;
• использовать прецизионные резисторы (допуск меньше 1%), чтобы получить более предсказуемые измерения. Если вам критична точность измерений, имейте в виду, что самонагревание термистора может повлиять на измерения; в данной статье самонагрев не компенсируется.

Конечно, термисторы – это только один из датчиков, используемых для измерения температуры. Другой популярный выбор – это микросхемы датчиков (пример работы с одной из них описан здесь). В этом случае вам не придется иметь дело с линеаризацией и сложными уравнениями. Два других варианта – это термопара и инфракрасный тип датчика; последний может измерять температуру без физического контакта, но он уже не так дешев.

Надеюсь, статья оказалась полезной. Оставляйте комментарии!

Источник