knigechka
Сайт содержит тексты редких методических пособий, лабораторных и контрольных работ. Вообщем, то что трудно найти в сети но очень нужно для подготовки к экзаменам, в частности на заочной форме обучения.
1.4.Нормальные алгоритмы А.А.Маркова
1.4.1.Основные понятия
Эта алгоритмическая система, основанная на соответствии между словами в абстрактном алфавите, включает в себя объекты двоякой природы:
элементарные операторы и
Элементарные операторы (ЭО) – достаточно просто задаваемые алфавитом операторы, с помощью последовательного выполнения которых реализуются любые алгоритмы в рассматриваемой алгоритмической системе.
Элементарные распознаватели (ЭР) служат для распознавания наличия тех или иных свойств перерабатываемой информации и для изменения, в зависимости от результатов распознавания, последовательности, в которой следуют друг за другом элементарные операторы.
Для указания набора элементарных операторов и порядка их следования при задании конкретного алгоритма удобно пользоваться ориентированными графами особого рода, называемыми граф — схемами соответствующих алгоритмов (ГСА).
ГСА — конечное множество соединенных между собой вершин, называемых узлами ГСА. Каждому узлу, кроме входа и выхода, сопоставляется какой-либо элементарный оператор или распознаватель.
Из каждого узла, которому сопоставлен распознаватель, исходят только две дуги. Из выходного узла не исходит ни одной дуги. Число дуг, входящих в ГСА может быт любым.
Рассмотрим на примере общий вид граф — схемы:
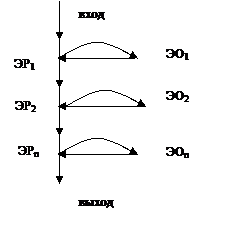 |
В общем случае число дуг, входящих в вершины – распознаватели, может быть любым.
Алгоритм, определенный граф-схемой, работает следующим образом:
-входное слово поступает на вход и двигается по направлениям, указанным стрелками;
-при попадании слова в распознавательный осуществляется проверка условия, сопоставленного этому узлу;
-при выполнении условия слово направляется в операторный узел, при невыполнении – к следующему распознавателю. Иногда стрелки обозначаются соответственно + и -. Если входное слово, поданное на вход граф-схемы, проходя через узлы схемы и преобразуясь, попадает через конечное число шагов на выход, то считается, что алгоритм применим к слову Р. Если преобразование слова Р и движение его по граф-схеме продолжается бесконечно долго, то считается, что алгоритм не применим к слову Р, т.е. Р не входит в область определения алгоритма.
В нормальных алгоритмах Маркова в качестве ЭО используется оператор подстановки, а качестве ЭР – распознаватель вхождений, который проверяет условие, имеет ли место вхождение рассматриваемого слова Р1 в качестве подслова некоторого заданного слова q.
Оператор подстановки заменяет первое слева вхождение слова Р1 в слове q на некоторое заданное слово Р2. Оператор подстановки задается обычно в виде двух слов, соединенных стрелкой: Р1 à Р2.
Например, для слова abcabca применение подстановки bc à cb приводит к следующему:
abcabca à acbabca à acbacba.
Последовательность слов P1,P2,…,Pn , получаемых в процессе реализации алгоритма, называется дедуктивной цепочкой, ведущей от слова Р1 к слову Pn.
Алгоритмы, которые задаются графами, составленными исключительно из распознавателей вхождений слов и операторов подстановки, называются обобщенными нормальными алгоритмами (ОНА). При этом предполагается, что к каждому оператору подстановки ведет только одна дуга, исходящая из соответствующего распознавателя.
Рассмотрим пример обобщенного нормального алгоритма, заданного подстановками:
Работу алгоритма проанализируем для входного слова bcbaab.
Граф-схема алгоритма имеет вид:
 |
В предлгаемом примере цепочка преобразований будет следующей:
bcbaab à bcabab à bcaabb àbaaabb àbaaaac.
Рассмотрев обобщенные алгоритмы, перейдем к характеристике собственно нормальных алгоритмов.
Нормальными алгоритмами Маркова (HA) называются такие обобщенные алгоритмы, граф-схемы которых удовлетворяют следующим условиям:
1.Все узлы, соответствующие распознавателям, упорядочиваются с помощью их нумерации от 1 до n;
2.Дуги, исходящие из узлов, соответствующих операторам подстановки, подсоединяются либо к узлу соответствующему первому распознавателю, либо к выходному узлу. В первом случае подстановка называется обычной, во втором — заключительной;
3.Входной узел подсоединяется дугой к первому распознавателю.
Нормальные алгоритмы принято задавать упорядоченным множеством подстановок для выходных операторов данного алгоритма, называемых схемой алгоритма.
Обычные подстановки записываются, как и в обобщенных нормальных алгоритмах: P1àP2, а заключительные P1à . P2.
Процесс подстановки заканчивается, лишь тогда, когда ни одна из подстановок схемы не применима к конкретному слову или когда выполнена (первый раз) заключительная подстановка.
Граф-схема НА в обобщенном виде может быть представлена следующим образом:
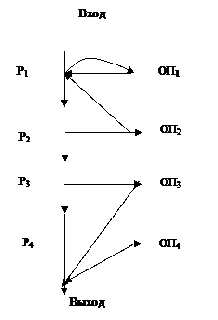 |
Рассмотрим пример представления нормального алгоритма Маркова для реализации операции сложения целых чисел, где числа представлены последовательностью соответствующего числа единиц.
Алфавит для этого преобразования включает в себя два символа: + и 1.
Схема подстановки: ‘1+1’à’11’, ‘1’ à. ‘1’.
Граф – схема нормального алгоритма Маркова в этом случае принимает вид:
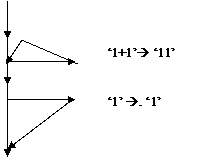 |
Преобразование входного слова в нашем случае имеет вид:
1.4.2.Принцип нормализации
Наличие в нормальных алгоритмах двух видов подстановки – необходимое условие универсальности, т.е. возможности построения нормального алгоритма, эквивалентного любому наперёд заданному алгоритму.
Принцип нормализации может быть сформулирован таким образом:
для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм над алфавитом А.
Понятие нормального алгоритма над алфавитом означает следующее:
в ряде случаев не удается построить нормальный алгоритм, эквивалентный данному в алфавите А, если использовать в подстановках только буквы этого алфавита. Однако, можно расширить требуемый нормальный алгоритм, производя расширение алфавита А, то есть добавляя к алфавиту А несколько новых букв.
В этом случае принято говорить, что построенный алгоритм является алгоритмом над алфавитом А, хотя алгоритм по-прежнему будет применяться к словам в исходном алфавите А.
Одноместная частичная словарная функция F(p), заданная в алфавите А, называется нормально вычислимой, если существует алгоритм N над алфавитом А такой, что для каждого слова р в алфавите А выполняется равенство F(p) =N(p).
Например, пусть в словаре A=<0,1>может быть записано слово р любой длины. Необходимо реализовать функцию F(p)=pa с использованием нормального алгоритма Маркова.
Рассмотрим вычисление функции F(p) для слова р=0110.
N-нормальный алгоритм в более широком алфавите <0,1,2>, имеющий схему:
20¾>02, 21¾>12, 2¾>.a, 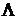
После первого шага подстановки мы получим слово 20110. Каждый следующий шаг будет сдвигать “2” на одно место вправо. После пятого шага получим:
Таким образом, алгоритм над алфавитом <0,1>вычислит функцию ра, заданную в алфавите <0,1>. В частности, алгоритм со схемой 
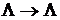
Математически доказать принцип нормализации невозможно, поскольку понятие произвольного алгоритма не является строго определенным математическим понятием.
Условимся называть тот или иной алгоритм нормализуемым, если можно построить эквивалентный ему нормальный алгоритм и ненормализуемым в противном случае.
Принцип нормализации теперь может быть высказан в следующей форме: все процессы, являющиеся алгоритмами — нормализуемы.
Справедливость этого принципа основывается на том, что все известные алгоритмы являются нормализуемыми, а способы композиции алгоритмов, позволяющие строить новые алгоритмы из уже известных, не выводят за пределы класса нормализации.
1.4.3.Основные способы композиции алгоритмов
При суперпозиции двух алгоритмов А и В выходное слово алгоритма А рассматривается как входное слово алгоритма В. Результат суперпозиции можно представить в виде C(p)=B(A(p)).
Суперпозиция может выполняться для любого конечного числа алгоритмов.
Графически суперпозиция алгоритмов А и В представлена ниже:
 |
Объединением алгоритмов А и В в одном и том же алфавите Х называют алгоритм С в том же алфавите, преобразующий любое слово Р, содержащееся в пересечении областей определения алгоритмов А и В, в записанные рядом слова А(р) и В(р). На всех остальных словах этот алгоритм считается неопределенным.
Например, дано: X=
Тогда, A(aba)=baa, B(aba)=aab и C(aba)=baaaab.
Разветвление алгоритмов представляет собой композицию алгоритмов А, В и С. Обозначая результат этой композиции D, будем считать, что область определения D совпадает с пересечением областей определения всех трех алгоритмов А, В, С, а для любого слова р из этого пересечения
 |
D(p)= A(p), если C(p) = e
B(p), если С(p) # e, где e – пустая строка (слово).
Рассмотрим действие алгоритма D на строки:
Повторение(итерация) представляет собой композицию двух алгоритмов А и В с результатом С.
Для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, перерабатываемое алгоритмом В в некоторое фиксированное слово.

Алгоритм А Алгоритм В
Все рассмотренные композиции нормальных алгоритмов приводят к получению также нормального алгоритма.
1.4.4.Задача построения универсального алгоритма
Универсальный алгоритм должен выполнять работу любого нормального алгоритма, если задана его схема.
Для задания универсального алгоритма U может быть применена следующая схема.
Фиксируется некоторый стандартный алфавит С (допустим двоичный). Для всех других возможных алфавитов задается некоторый способ их кодирования в алфавите С. Для символов, употребляемых в схемах нормальных алгоритмов (ввод, вывод, знак подстановки, разделитель операторов подстановки), отводятся отдельные коды.
Тогда, если задан некоторый алгоритм N, его кодируют одним словом Nu, называемым изображением алгоритма N в стандартном алфавите.
Входное слово P кодируют в слово Pu, называемое изображением слова.
Например, задан алгоритм N
Изображением этого алгоритма в алфавите из десятичных цифр и при кодировании:
Pu=010 010 020 010.
Справедлива следующая теорема Маркова об универсальноь нормальном алгоритме:
Существует такой универсальный алгоритм U, который для любого НА N и любого входного слова Р из области определения алгоритма N переводит слово NuPu , полученное приписыванием изображения слова P(Pu) к изображению алгоритма N(Nu), в слово Ru, являющегося изображением соответствующего выходного слова R=N(P), в которое алгоритм N перерабатывает слово Р.
Если же слово Р выбирается так, что алгоритм N к нему не применим, то и универсальный алгоритм U не применим к слову NuPu .
Эта теорема имеет большое значение, так как из нее вытекает возможность построения машины, которая может выполнять работу любого нормального алгоритма, а значит в силу принципа нормализации – работу любого произвольного алгоритма.
Программой машины в этом случае должно быть слово Nu (изображение данного алгоритма), а исходными данными слово Pu.
После нумерации входных и выходных слов любой нормальный алгоритм может быть реализован в виде частично рекурсивной функции и, наоборот, любой алгоритм, реализуемый с помощью частично рекурсивной функции, оказывается эквивалентным некоторому нормальному алгоритму.
Источник
Способы композиции нормальных алгоритмов:
Суперпозиция алгоритмов. При суперпозиции двух алгоритмов A и B выходное слово первого алгоритма рассматривается как входное слово второго алгоритма. Результат суперпозиции С может быть представлен в виде C(P) = B(A(P))
Объединение алгоритмов. Объединением алгоритмов A и B в одном и том же алфавите называется алгоритм C, преобразующий любое слово P, содержащееся в пересечении областей определения алгоритма A и B в записанные рядом слова A(P) и B(P)
Разветвление алгоритмов. Разветвление представляет собой композицию D трёх алгоритмов A,B и C, причём область определения алгоритма D является пересечением областей определения трёх алгоритмов A,B,C.
Итерация (повтор). Представляет собой такую композицию C двух алгоритмов A и B, что для любого входного слова P, соответствующего слова C(P), получается в результате последовательного многократного применения алгоритма A до тех пор, пока не получится слово, образуемое алгоритмом B.
Нормальные алгоритмы Маркова являются не только средством теоретических построений, но и основой специализированного языка программирования, применяемого как язык символьных преобразований при разработке систем искусственного интеллекта.
Рекурсивные функции.
Ещё одним подходом к проблеме формализации понятия алгоритма являются т.н. рекурсивные функции. Исторически этот подход возник первым, по этому в математических исследованиях, посвящённых алгоритмам, он имеет наибольшее распространение.
Рекурсией называется способ задания функции, при котором значении функции при определённом значении аргументов выражается через уже заданные значения функции, при других значениях аргументов.
Применение рекурсивных функций в теории алгоритмов основано на идее нумерации слов в произвольном алфавите последовательными числами.
Т.о. любой алгоритм можно свести к вычислению значений некоторой функции, при целочисленном значении аргумента.
Введём несколько понятий.
Пусть X и Y – два множества. Частичной функцией (или отображением из X в Y) будем называть пару , состоящее из подмножества D(f), содержащее D(f) € X.
Через n будем обозначать множество значений чисел (N) n .
Частичная функция f называется вычислимой, если можно указать такой алгоритм, который для входного набора XC(N) n даёт на выходе f(X), если X € D(f). И 0, если X не принадлежит D(f).
В этом отрезке неформальное понятие алгоритма оказывается связанным с понятием вычислимости функции.
Вместо алгоритмов далее будут изучаться свойства вычислимых функций.
Частная функция из (N) m полувычислима, если можно указать такой алгоритм, который для входного набора X(N) n лежит в области определения.
Очевидно, что вычислимые функции полувычислимы, а всюду определённые полувычилсимые функции вычислимы.
Частичная функция f называется ни вычислимой, ни полувычислимой. Фундаментальным открытием теории вычислимости является т.н. тезис Чёрча, который в слабейшей форме имеет следующий вид: можно явно указать:
семейство простейших полувычисимых функций;
Семейства элементарных операций, которые позволяют строить по одним полувычислимым функциям другие полувычислимые функции с тем свойством, что любая полувычислимая функция получается за конечное число шагов, каждый из которых стостоит в применении одной из элементарных операций к ранее построенным или к простейшим функциям.
Suc:N → N ( suc(x) = x+1 – определение следующего за x числа).
Определение размерности области определения функции
Pr n (x1…xn)=x2 – проекция области определения на одну из переменных.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник