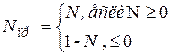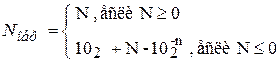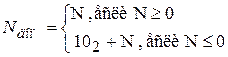Способы кодирования отрицательных целых чисел сообщение

Кодирование отрицательных чисел.

Отрицательные числа в ЭВМ представляются в прямом, дополнительном и обратном кодах.

При представлении числа в прямом коде код числа в разрядной сетке из n разрядов совпадает с самим числом.

В двоичной системе счисления знаки кодируются следующим образом: «+» цифрой 0, «-« цифрой 1. Знаковый разряд располагается слева от значащих цифр числа, то есть это крайний левый разряд в представление числа. При таком подходе введение знакового разряда уменьшает диапазон представления положительных и отрицательных чисел. Вес знакового разряда соответствует весу старшего разряда разрядной сетки. Значащие разряды числа занимают n-1 разряд. Диапазон представления положительных чисел 0 X 2 n -1 –1, а отрицательных 0 X -(2 n -1 – 1).

X, при X ³ 0

[X] _пр = (7)

q n -1 +lXl, при X £ 0

где q n -1 величина, равная весу старшего разряда (для дробных чисел q n -1 =1).

Обратите внимание на то, что запись числа в форме (7) приводит к двум равнозначным формам записи нуля – «положительной» и «отрицательной».

Примеры: представить в прямом коде следующие числа:

3. а) Х1 = +В13; б) Х3 = +0.В13

Х2 = -В13 ; Х4 = -0.В13

Ответы:

1. q n -1 = 2 5 = 100000

Здесь и далее знаковый разряд будет отмечаться подчёркиванием.

Точка в результате используется нами только для указания того, что число представлено правильной дробью и, следовательно, всегда меньше 1. Этот знак не является частью числа и в машинном представлении опускается.

2. q n -1 = 8 3 = 1000

3. q n -1 = 16 3 = 1000

Дополнительный код отрицательного числа представляет собой дополнение модуля исходного числа Х до q n , где n — количество разрядов целой части числа Х. Для правильной дроби q n = 10 в соответствующей системе счисления.

Поэтому для целого числа:

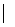
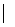
q n — X , при X =0

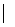
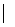
1- X , при X n = 2 6 = 1000000

а) [X1]_доп= 011011; [X2] _доп =1000000 – 011011= 100101;

или [X2] _доп = 100100 + 000001 = 100101;

б) [X3] _доп = 0.11011 [X4] _доп = 10.00000 – 0.11011 =1.00101;

или [X4] _доп = 1.00100 + 0.000001 = 1.00101

2. q n = 84 = 10000

3. q n +1 = 16 4 =1 0000

[X2] _доп = 1.F4ЕС + 0.0001 = 1.F4ED

[X4] _доп = 1.4ЕС + 0.001 = 1.4ED

Обратный код отрицательных чисел представляется как дополнение модуля исходного целого числа Х до q n +1 и модуля исходной правильной дроби до 1 0 в соответствующей СС без единицы младшего разряда числа.

Если к представлению исходного числа в обратном коде прибавить единицу младшего разряда, то получим исходное число в дополнительном коде.

Источник

Кодирование отрицательных чисел

Для выполнения арифметических операций двоичные числа кодируются специальными машинными кодами: прямыми, дополнительными и обратными, позволяющими заменить операции вычитания операциями суммирования, что упрощает построение арифметическо-логических устройств.

Прямой код. Представление двоичных чисел в прямом коде основано на подаче их в абсолютном виде с соответствующим знаком: плюсом (0) или минусом (1).

Формула для образования прямого двоичного числа имеет вид:

Ноль в прямом коде может выглядеть двояко, т.е. может быть и положительным и отрицательным

Прямой код используется для хранения чисел в устройствах ввода и вывода информации, а также при выполнении операции умножения.

Обратный код. Формула для образования обратного кода имеет вид

Пример 2. N = – 0.101011₂, N_обр =10₂ – 0.101011 – 0.000001 = –1.010100

Обратный код положительного числа полностью совпадает с изображением числа в прямом коде. Для получения обратного кода отрицательного числа, нужно в знаковом разряде этого числа поставить единицу, а в числовых разрядах нули заменить единицами, а единицы — нулями.

В обратном коде нуль изображается неоднозначно:

Дополнительный код. Формула для образования дополнительного кода двоичного числа имеет вид

Пример 3. N = 0.1010 = 10₂ + (– 0.1010) = – 1.0101.

Дополнительный код положительного числа полностью совпадает с изображением числа в прямом коде.

Чтобы записать отрицательное число в дополнительном коде, нужно в знаковом разряде этого числа поставить единицу, во всех числовых разрядах нули заменить единицами, единицы – нулями и к полученному результату прибавить единицу младшего разряда.

В дополнительном коде отрицательный нуль отсутствует.

Источник

Кодирование числовой информации

Введение

Если у вас возникли какие-либо вопросы при изучении темы «Кодирование числовой информации», то звоните мне и записывайтесь на первый репетиторский урок по информатике и ИКТ. На моих индивидуальных уроках мы с вами закроем текущие пробелы в ваших знаниях и прорешаем колоссальное количество всевозможных тематических упражнений.

Общие понятие о числовой информации

Думаю, что превалирующее число школьников и студентов знает фразу: «Математика – царица всех наук!». А как известно, математика очень интенсивно оперирует числами, цифрами и действиями над числами.

Первый счет появился много тысячелетий назад, так как даже в очень древние времена люди столкнулись с потребностью в счете. Его возникновение связано с желанием человека проинформировать своих соплеменников о количестве обнаруженных им объектов, предметов. По началу люди просто делили предметы по принципу один-много. То есть не было обозначения для двух, трех, десяти и более различных предметов. Их просто обозначали в количественном отношении как много.

Постепенно люди научились подключать к арифметическому счету пальцы на своих руках. С их помощью можно было считать до пяти, а если использовать обе руки, то до десяти различных предметов. Именно десятичная система счисления получило свое развитие на основе использования при счете пальцев рук.

Вернемся в настоящий временной континуум. Для современного человека знания, позволяющие считать предметы и записывать числа, являются обязательными. Арифметика изучается в школе с первого класса. Цифры, используя которые мы записываем числа, называются арабскими. Алфавит арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего десять различных цифр или состояний.

Числа можно классифицировать на две фундаментальные группы:

Дробные или действительные числа.

Каждое число из представленных групп может быть либо:

Примеры различных десятичных чисел:

-56 — целое отрицательное число;

12.78 — действительное положительное число;

0.0 — действительное число, равное нулю;

12000 — целое положительное число.

Наша цель – понять, каким образом производится кодирование числовой информации, выраженной целыми или дробными числами, которые являются положительными, отрицательными или равными нулю. Другими словами, мы должны понять, как персональный компьютер хранит, обрабатывает, копирует числа на «своем» уровне.

Свойства числовой информации

Конечность. Информация, выраженная числовым значением, должна быть конечной. Процессор персонального компьютера не сможет обработать число, которое не является конечным или завершенным. То есть прежде чем приступить к кодированию числовой информации, процессор должен быть уверен, что данное значение записано полностью и не будет изменено пользователем.

Понятность. Если мы говорим о кодировании числовой информации, которая представлена десятичным числом, то необходимо, чтобы само число состояло из элементов, которые будут понятны исполнителю при кодировании. Исполнителем является, в строгом приближении, процессор персонального компьютера. Например, число 129 состоит из трех цифр: 1, 2 и 9. Каждое из этих цифр входит в состав арабского алфавита. Если мы представим числовую информацию в виде значения 89J1’4, то подобное значение будет некорректно обработано процессором и он выдаст исключение, то есть сгенерирует ошибку. Почему? Потому что входное число 89J1’4 состоит из элементов: 8, 9, J, 1, ‘, 4, не каждое из которых входит в состав арабского алфавита. Например, элементы J и ‘ не являются арабскими цифрами.

Приведенные два свойства являются ключевыми в алгоритмах кодирования числовой информации. Пожалуй, еще стоит отметить неосновное свойство – размер числа. Но в современном мире мощности персональных компьютеров постоянно увеличиваются и самые эффективные процессоры способы обрабатывать огромные значения.

Способы кодирования числовой информации

Сразу необходимо твердо уяснить следующее: процессор персонального компьютера взаимодействует с любыми данными исключительно на уровне цепочек, состоящих из 0 и 1. Набор нулей и единиц называют двоичным или бинарным кодом. То есть любые текстовые, символьные или числовые значения, которые понятны простому человеку, процессор преобразует в двоичный код. Следовательно, наша задача – научиться переводить числовые значения в бинарное представление, состоящее из цепочек 0 и 1.

Для полного осознания алгоритма кодирования числовой информации необходимо очень хорошо уяснить понятие «Машинное слово». Возможно вы слышали, что иногда пользователи говорят, что на их компьютерах установлена 32-х разрядная или 64-х разрядная система Microsoft Windows. Именно значение разрядности (в приведенном примере это 32 или 64) и отвечает за то, сколько бит информации будет выделено для хранения какого-либо математического значения при кодировании числовой информации. То есть, если нам дано положительное целое число 25, то при преобразовании его в бинарный код, ему будет выделено 32 или 64 бита. Также напомню, что один байт информации состоит из 8 битов.

Далее по тексту я буду работать на уровне 16-и разрядной системы. То есть любое кодирование числовой информации будет представлено с использованием машинного слова в 16 бит.

Кодирование целых положительных чисел

Это наиболее простой способ кодирования данных, так как для его реализации необходимо уметь переводить числа из десятичной системы счисления в двоичную систему. Ниже я приведу таблицу, в которой покажу кодирование целых положительных чисел различной значности.

Исходное десятичное число

Закодированное десятичное число в двоичном коде

Источник

Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа

Прямой код

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.

Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:

0 0001101 – положительное число
1 0001101 – отрицательное число

Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).

При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.

Дополнительный код

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.

Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.

Далее следует прибавить единицу к получившемуся инверсией числу:

1 1110011 + 1 = 1 1110100

В итоге и получается число, которое принято называть дополнительным кодом числа.

Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.

Источник