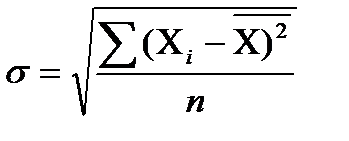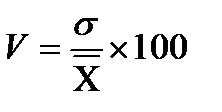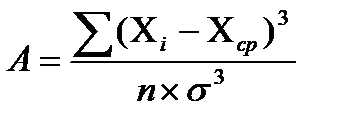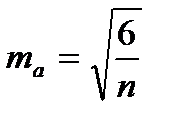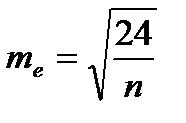Способы изучения стохастических взаимосвязей

Глава 7 СПОСОБЫ ИЗУЧЕНИЯ СТОХАСТИЧЕСКИХ (КОРРЕЛЯЦИОННЫХ) ВЗАИМОСВЯЗЕЙ В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ — Анализ хозяйственной деятельности предприятия

Глава 7 СПОСОБЫ ИЗУЧЕНИЯ СТОХАСТИЧЕСКИХ (КОРРЕЛЯЦИОННЫХ) ВЗАИМОСВЯЗЕЙ В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ

7.1. Понятие стохастической связи и задачи корреляционного анализа

Сущность стохастических взаимосвязей между показателями. Отличия стохастических связей от функциональных. Способы исследования зависимостей в стохастическом факторном анализе. Условия применения и задачи корреляционного анализа.

В предыдущих главах рассматривалась методика решения задач детерминированного факторного анализа. Однако на практике далеко не все экономические явления и процессы могут изучаться с помощью этой методики, так как в большинстве случаев их нельзя свести к функциональным зависимостям, когда величине факторного показателя соответствует единственная величина результативного показателя.

Чаще в экономических исследованиях встречаются стохастические зависимости, которые отличаются приблизительностью, неопределенностью. Они проявляются только в среднем по значительному количеству объектов (наблюдений). Здесь каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Например, увеличение фондовооруженности труда рабочих дает разный прирост производительности труда на разных предприятиях даже при очень выравненных прочих условиях. Это объясняется тем, что все факторы, от которых зависит производительность труда, действуют в комплексе, взаимосвязано. В зависимости от того, насколько оптимально сочетаются разные факторы, будет неодинаковой степень воздействия каждого из них на величину результативного показателя.

Взаимосвязь между исследуемыми факторами и результативным показателем проявится, если взять для исследования большое количество наблюдений (объектов) и сравнить их значения. Тогда в соответствии с законом больших чисел влияние других факторов на результативный показатель сглаживается, нейтрализуется. Это дает возможность установить связь, соотношения между изучаемыми явлениями.

Значит, корреляционная (стохастическая) связь — это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Отличают парную и множественную корреляцию.

Парная корреляция — это связь между двумя показателями, один из которых является факторным, а другой — результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Для исследования стохастических соотношений используются следующие способы экономического анализа, с которыми мы уже знакомились в предыдущих главах: сравнение параллельных и динамических рядов, аналитические группировки, графики. Однако они позволяют выявить только общий характер и направление связи. Основная же задача факторного анализа — определить степень влияния каждого фактора на уровень результативного показателя. Для этой цели применяются способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа и т.д.

Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями.

Необходимые условия применения корреляционного анализа.

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов).

2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Источник

Тема 6. Способы изучения стохастических взаимосвязей в экономическом анализе

Стохастическая (корреляционная) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений, тогда влияние других факторов сглаживается.

Различают парную и множественную корреляцию.

Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным.

Множественная корреляция — возникает от взаимодействия нескольких факторов с результативным показателем.

Для изучения стохастических зависимостей используют способы:

— сравнения параллельных и динамических рядов;

Эти способы выявляют характер и направление связи.

Для измерения влияния факторов в стохастическом анализе используются приемы корреляционного анализа.

Условия применения корреляционного анализа:

— наличие большого количества наблюдений о величине факторных и результативных показателей;

— факторы должны иметь количественное измерение.

Применение корреляционного анализа позволяет:

— определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

— установить относительную степень зависимости результативного показателя от каждого фактора (тесноту связи);

— оценить эффективность деятельности анализируемого предприятия по сравнению со средним уровнем (по отрасли, региону и т.п.) путем сравнения фактического и рассчитанного из уравнения регрессии значения результативного показателя).

Этапы корреляционного анализа:

1. отбор факторов для анализа;

требования к факторам: — наличие причинно – следственной связи с результативным показателем;

— в многофакторную корреляционную модель необходимо отбирать только значимые факторы, которые имеют критерий надежности по Стьюденту не меньше табличного;

— в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем носит криволинейный характер;

— не рекомендуется включать в модель взаимосвязанные факторы (парный коэффициент корреляции не должен быть больше 0,85);

— не рекомендуется включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.

2. сбор исходной информации по каждому факторному и результативному показателю; информация должна быть проверена на достоверность, однородность и соответствие закону нормального распределения;

Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.

Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической:

Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической:

Если вариация не превышает 10%, то изменчивость незначительная;

10-12% — средняя; 20-33% — значительная; если больше 33%, то информация считается неоднородной, необходимо исключить нетипичные наблюдения.

На основании максимального значения V определяют необходимый объем выборки:

, где n – необходимый объем выборки,

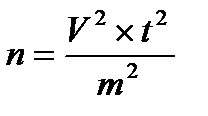
V – максимальный коэффициент корреляции в %,

t – показатель надежности связи, который при уровне вероятности 0,05 равен 1,96 (?),

m – показатель точности расчетов, % (для экономических расчетов 5-8%).

Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.

Показатель асимметрии (А) и его ошибка :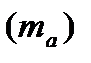

Показатель эксцесса (Е) и его ошибка :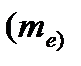

В симметричном распределении А=0. Отклонение от нуля указывает на наличие асимметрии в распределении данных около средней величины. Если асимметрия отрицательная, значит преобладают данные с большими значениями; если положительная – чаще встречаются небольшие значения.

В нормальном распределении Е=0. Если Е>0, то вершина острая (данные густо сгруппированы около среднего значения); если Е

Дата добавления: 2017-03-29 ; просмотров: 1281 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Способы изучения стохастических взаимосвязей

Глава 7 СПОСОБЫ ИЗУЧЕНИЯ СТОХАСТИЧЕСКИХ (КОРРЕЛЯЦИОННЫХ) ВЗАИМОСВЯЗЕЙ В АНАЛИЗЕ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ

Понятие стохастической связи.

Задачи корреляционного анализа.

Способы изучения парной корреляции.

Методика множественного корреляционного анализа.

Методика оценки и практического применения результатов корреляционного анализа.

7.1. Понятие стохастической связи и задачи корреляционного анализа

Сущность стохастических взаимосвязей между показателями. Отличия стохастических связей от функциональных. Способы исследования зависимостей в стохастическом факторном анализе. Условия применения и задачи корреляционного анализа.

В предыдущих главах рассматривалась методика решения задач детерминированного факторного анализа. Однако на практике далеко не все экономические явления и процессы могут изучаться с помощью этой методики, так как в большинстве случаев их нельзя свести к функциональным зависимостям, когда величине факторного показателя соответствует единственная величина результативного показателя.

Чаще в экономических исследованиях встречаются стохастические зависимости, которые отличаются приблизительностью, неопределенностью. Они проявляются только в среднем по значительному количеству объектов (наблюдений). Здесь каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Например, увеличение фондовооруженности труда рабочих дает разный прирост производительности труда на разных предприятиях даже при очень выравненных прочих условиях. Это объясняется тем, что все факторы, от которых зависит производительность труда, действуют в комплексе, взаимосвязано. В зависимости от того, насколько оптимально сочетаются разные факторы, будет неодинаковой степень воздействия каждого из них на величину результативного показателя.

Взаимосвязь между исследуемыми факторами и результативным показателем проявится, если взять для исследования большое количество наблюдений (объектов) и сравнить их значения. Тогда в соответствии с законом больших чисел влияние других факторов на результативный показатель сглаживается, нейтрализуется. Это дает возможность установить связь, соотношения между изучаемыми явлениями.

Значит, корреляционная (стохастическая) связь — это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Отличают парную и множественную корреляцию.

Парная корреляция — это связь между двумя показателями, один из которых является факторным, а другой — результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Для исследования стохастических соотношений используются следующие способы экономического анализа, с которыми мы уже знакомились в предыдущих главах: сравнение параллельных и динамических рядов, аналитические группировки, графики. Однако они позволяют выявить только общий характер и направление связи. Основная же задача факторного анализа — определить степень влияния каждого фактора на уровень результативного показателя. Для этой цели применяются способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа и т.д.

Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями.

Необходимые условия применения корреляционного анализа.

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов).

2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет решить следующие задачи:

1) определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), то есть определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

2) установить относительную степень зависимости результативного показателя от каждого фактора.

Исследование корреляционных соотношений имеет огромное значение в АХД. Это проявляется в том, что значительно углубляется факторный анализ, устанавливаются место и роль каждого фактора в формировании уровня исследуемых показателей, углубляются знания об изучаемых явлениях, определяются закономерности их развития и как итог — точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятий и более полно определяются внутрихозяйственные резервы.

7.2. Использование способов парной корреляции для изучения стохастических зависимостей

Формы стохастической связи. Приемы обоснования уравнения связи. Порядок расчета параметров уравнения прямой, параболы, гиперболы. Методика расчета коэффициентов корреляции при прямолинейной и криволинейной формах зависимости. Интерпретация результатов корреляционно-регрессионного анализа. Практическое их использование.

Одной из основных задач корреляционного анализа является определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейной, криволинейной и т.д.). Это играет важную роль в корреляционном анализе, потому что от правильного выбора уравнения регрессии зависит ход решения задачи и результаты расчетов.

Обоснование уравнения связи делается с помощью сопоставления параллельных рядов, группировки данных и линейных графиков. Размещение точек на графике покажет, какая зависимость образовалась между изучаемыми показателями: прямолинейная или криволинейная.

Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой:

где х — факторный показатель; Y — результативный показатель;

а и b — параметры уравнения регрессии, которые требуется отыскать.

Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание значений результативного показателя. В качестве примера для иллюстрации корреляционного анализа прямолинейной зависимости могут быть использованы сведения об изменении урожайности зерновых культур (Y) в зависимости от качества пахотной земли (х) (см. табл. 4.7).

Значения коэффициентов а и b находят из системы уравнений, полученных по способу наименьших квадратов. В данном случае система уравнений имеет следующий вид:

где п — количество наблюдений (в нашем примере — 20).

Значения рассчитываются на основе фактических исходных данных (табл. 7.1).

Подставив полученные значения в систему уравнений, получим

[900а+41500b= 22 900.

Умножив все члены первого уравнения на 45(900/20), получим следующую систему уравнений:

[900a + 40 500b = 22 500;

Отнимем от второго уравнения первое. Отсюда 1000b = 400; b = 0,4,

Таким образом, уравнение связи, которое описывает зависимость урожайности от качества почвы, будет иметь вид:

Коэффициент а — постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр b показывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения. В данном примере с увеличением качества почвы на один балл урожайность зерновых культур повышается в среднем на 0,4 ц/га.

Подставив в уравнение регрессии соответствующие значения х, можно определить выравненные (теоретические) значения результативного показателя (Y) для каждого хозяйства. Например, чтобы рассчитать урожайность зерновых культур для первого хозяйства, где качество почвы оценивается 32 баллами, необходимо это значение подставить в уравнение связи:

Yx= 7+0,4х32= 19,8 ц/га.

Полученная величина показывает, какой была бы урожайность при качестве почвы 32 балла, если бы данное хозяйство использовало свои производственные возможности в такой степени, как в среднем все хозяйства района. Аналогичные расчеты сделаны для каждого хозяйства. Данные приведены в последней графе табл. 7.1. Сравнение фактического уровня урожайности с расчетным позволяет оценить результаты работы отдельных предприятий.

По такому же принципу решается уравнение связи при криволинейной зависимости между изучаемыми явлениями. Если при увеличении одного показателя значения другого возрастают до определенного уровня, а потом начинают снижаться (например, зависимость производительности труда рабочих от их возраста), то для записи такой зависимости лучше всего подходит парабола второго порядка:

В соответствии с требованиями метода наименьших квадратов для определения параметров а, b и с необходимо решить следующую систему уравнений:

Значения находят на основании исходных данных (табл. 7.2).

Подставив полученные значения в систему уравнений, получим

Параметры а, b и с находят способом определителей или способом исключения. Используем способ определителей. Сначала найдем общий определитель:

затем частные определители а, b и с:

Уравнение параболы будет иметь следующий вид:

Yx = -2,67 + 4,424x — 0,56 lx2.

Параметры полученного уравнения экономического смысла не имеют. Если подставить в данное уравнение соответствующие значения х, то получим выравненные значения производительности труда в зависимости от возраста рабочих. Результаты приведены в последней графе табл. 7.2.

Из таблицы видно, что производительность труда рабочих повышается до 40-летнего возраста, после чего начинает снижаться. Значит, те предприятия, которые имеют больше работников 30 — 40-летнего возраста, будут иметь и более высокие показатели производительности труда при прочих равных условиях. Этот фактор необходимо учитывать при планировании уровня производительности труда и при подсчете резервов ее роста.

Довольно часто в экономическом анализе для записи криволинейных зависимостей используется гипербола:

Для определения ее параметров необходимо решить следующую систему уравнений:

Гипербола описывает такую зависимость между двумя показателями, когда при увеличении одной переменной значения другой увеличиваются до определенного уровня, а потом прирост снижается, например, зависимость урожайности от количества внесенного удобрения, продуктивности животных от уровня их кормления, себестоимости продукции от объема производства и т.д.

При более сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка и т.д.), а также квадратические, степенные, показательные и другие функции.

Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т.е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. Однако регрессионный анализ не дает ответа на вопрос: тесная это связь или нет, решающее воздействие оказывает данный фактор на величину результативного показателя или второстепенное?

Для измерения тесноты связи между факторными и результативными показателями определяется коэффициент корреляции.

В случае прямолинейной формы связи между изучаемыми показателями коэффициент корреляции рассчитывается по следующей формуле:

Подставляя значения в формулу (7.7), получаем

Коэффициент корреляции может принимать значения от О до ±1. Чем ближе его величина к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае величина коэффициента корреляции является существенной (r= 0,66). Это позволяет сделать вывод о том, что плодородие почвы — один из основных факторов, от которого в данном районе зависит уровень урожайности зерновых культур.

Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации (d = 0,435). Он показывает, что урожайность зерновых культур на 43,5% зависит от качества почвы, а на долю других факторов приходится 56,5% прироста урожайности.

Что касается измерения тесноты связи при криволинейной форме зависимости, то здесь используется не линейный коэффициент корреляции, а корреляционное отношение:

Показатель (7.8) является универсальным. Его можно применять при любой форме зависимости. Однако для определения его величины вначале необходимо решить уравнение регрессии и рассчитать выравненные значения результативного показателя (Ух), для чего в полученное уравнение нужно подставить значения х и х2 по каждой возрастной группе (табл. 7.3).

Подставив полученные значения в формулу (7.8), определим величину корреляционного отношения:

В заключение необходимо отметить, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, определить место и роль каждого фактора в изменении уровня исследуемого показателя.

7.3. Методика множественного корреляционного анализа

Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии шаговым способом. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэф-фициентов.

Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления.

Многофакторный корреляционный анализ состоит из нескольких этапов.

На первом, этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа.

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, то есть подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости.

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа.

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение.

Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Главная роль при отборе факторов принадлежит теории, а также практическому опыту анализа. При этом необходимо придерживаться следующих правил.

1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ же таких факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла.

2. При создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет.

3. Все факторы должны быть количественно измеримы, т.е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности.

4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер.

5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффицие

Источник