ТОПОГРАФИЧЕСКАЯ ПОВЕРХНОСТЬ И ЕЕ ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА



ОСНОВНЫЕ ПОНЯТИЯ
ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ. КРИВЫЕ ПОВЕРХНОСТИ
По геометрическим признакам все поверхности делят на две группы:
1) геометрически правильные поверхности, образованные по определенному геометрическому закону;
2) геометрически неправильные поверхности, образование которых не связано с геометрическими законами.
К первой группе поверхностей относят цилиндрическую, коническую, сферическую и другие, для точного изображения которых на чертеже требуется совершенно определенный минимум данных.
Поверхности второй группы изображаются только приближенно, причем изображение будет тем точнее, чем больше исходных данных приходится на единицу рассматриваемой поверхности. Ко второй группе наряду с другими относятся и все поверхности топографического порядка.
Поверхности, ограничивающие разного рода геологические тела, являются поверхностями топографического порядка. Однако в решении практических задач геологоразведочного производства эти поверхности часто аппроксимируются близкими по форме геометрически правильными поверхностями: многогранными, цилиндрическими, коническими и др.
Топографическую поверхность относят к геометрически неправильным поверхностям, так как она не имеет геометрического закона образования. Для характеристики поверхности определяют положение ее характерных точек относительно плоскости проекций.
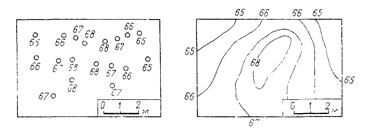
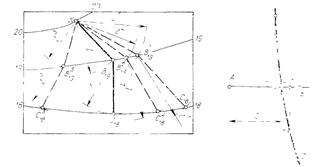
На рис. 5.1 дан пример плана участка топографической поверхности, на котором показаны проекции ее отдельных точек. Такой план хотя и дает возможность составить представление о форме изображаемой поверхности, однако отличается малой наглядностью. Чтобы придать чертежу большую наглядность и облегчить тем самым его чтение, проекции точек с одинаковыми отметками соединяют плавными кривыми линиями, которые называют горизонталями – изолиниями.
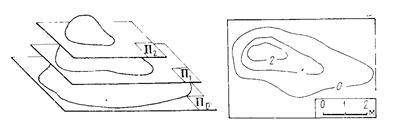
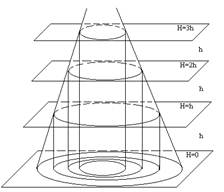
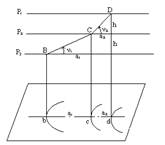
Горизонтали топографической поверхности иногда определяют и как линии пересечения этой поверхности с горизонтальными плоскостями, отстоящими друг от друга на одно и то же расстояние (рис. 5.2). Разность отметок у двух смежных горизонталей называют высотой сечения. Изображение топографической поверхности тем точнее, чем меньше разность отметок у двух смежных горизонталей. На топографических планах горизонтали замыкаются в пределах чертежа или вне его. На более крутых склонах поверхности проекции горизонталей сближаются, на пологих – их проекции расходятся.
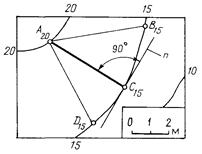
Кратчайшее расстояние между проекциями двух смежных горизонталей на плане называют заложением. На рис. 5.3 через точку А топографической поверхности проведено несколько отрезков прямых: |AB|, |AC| и |AD|. Все они имеют разные углы падения. Наибольший угол падения имеет отрезок |AC|, заложение которого имеет минимальное значение. Очевидно, он и будет являться проекцией линии падения поверхности в данном месте. Проекция этой линии перпендикулярна к касательной n, проведенной через точку C. На рис. 5.4 приводится пример построения проекции линии падения через заданную точку A. Из точки A100 , как из центра, проводят дугу окружности, касающуюся ближайшей горизонтали в точке B90. Точка B90 , лежащая на горизонтали h90 , будет принадлежать линии падения. Из точки B90 проводят дугу, касающуюся следующей горизонтали в точке C80, и т.д. Из чертежа видно, что линией падения топографической поверхности является ломаная линия, каждое звено которой перпендикулярно к горизонтали, проходящей через нижний, имеющий меньшую отметку, конец звена.
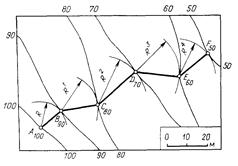
На рис. 5.5 дан пример построения проекции линии постоянного уклона, соединяющей кратчайшим путем точки A и C топографической поверхности. Проведение такого рода линий связано с проектированием технических сооружений на сильно пересеченном рельефе местности. Задачу решают в следующем порядке:
1) через точку A проводят ломанную линию постоянного уклона (AB 1 C 1 ), заложение l 1 которой берут произвольно. Отрезок, соединяющий заданную точку C с построенной точкой C 1 , является величиной несходимости точки C 1 с точкой C;
2) через точку A проводят несколько ломанных линий (AB 2 C 2 ), (AB 3 C 3 ) . причем их заложения l 2 , l 3 берут в сторону уменьшения (увеличения) заложения l 1 : l 2 1 , l 3 1 и т.д.;

3) строят кривую ошибок. На горизонтальной прямой от точки A откладывают заложения проведенных по поверхности линий: |AB 1 | = l 1 , |AB 2 | = l 2 , |AB 3 | = l 3 и т.д.
Через точки B 1 , B 2 , B 3 … проводят вертикальные линии, на которых откладывают величины несходимости точек C 1 , C 2 , C 3 … |C18C 1 18 | = |B 1 C 1 |, |C18C 2 18 | = |B 2 C 2 |, |C18C 3 18 | = |B 3 C 3 |.
Соединив точки C 1 , C 2 , C 3 … плавной линией p, отмечают точку B пересечения кривой ошибок с горизонтальной прямой. Отрезок [AB] является заложением l искомой линии.
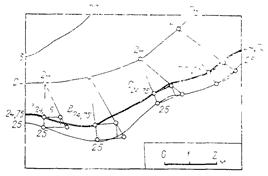
На рис. 5.6 дан пример построения дополнительной горизонтали поверхности с отметкой 24,75 м. Между горизонталями с отметками 24 и 25 м проводят отрезки прямых, на которых методом профиля находят точки с заданной отметкой. Полученные точки A, B, C … соединяют плавной линией.
В заключение следует заметить, что для построения точки, принадлежащей какой-либо из рассмотренных поверхностей, необходимо построить линию (прямую или кривую), лежащую на этой поверхности, и на ней отметить искомую точку.
Источник
Способы изображения рельефа



Основные формы рельефа. Несмотря на большое разнообразие неровностей земной поверхности, можно выделить основные формы рельефа: гора, котловина, хребет, лощина, седловина.
Гора (или холм) — это возвышенность конусообразной формы. Она имеет характерную точку — вершину, боковые скаты (или склоны) и характерную линию — линию подошвы. Линия подошвы — это линия слияния боковых скатов с окружающей местностью . На скатах горы иногда бывают горизонтальные площадки, называемые уступами.
Котловина — это углубление конусообразной формы. Котловина имеет характерную точку — дно, боковые скаты (или склоны) и характерную линию — линию бровки. Линия бровки — это линия слияния боковых скатов с окружающей местностью.
Хребет — это вытянутая и постепенно понижающаяся в одном направлении возвышенность. Он имеет характерные линии: одну линию водораздела, образуемую боковыми скатами при их слиянии вверху, и две линии подошвы.
Лощина — это вытянутое и открытое с одного конца постепенно понижающееся углубление. Лощина имеет характерные линии: одну линию водослива (или линию тальвега), образуемую боковыми скатами при их слиянии внизу, и две линии бровки.
Седловина — это небольшое понижение между двумя соседними горами; как правило, седловина является началом двух лощин, понижающихся в противоположных направлениях. Седловина имеет одну характерную точку — точку седловины, располагающуюся в самом низком месте седловины.
Существуют разновидности перечисленных основных форм, например, разновидности лощины: долина, овраг, каньон, промоина, балка и т.д. Иногда разновидности основных форм характеризуют особенности рельефа конкретного участка местности, например, в горах бывают пики — остроконечные вершины гор, ущелья, теснины, щеки, плато, перевалы и т.д.
Вершина горы, дно котловины, точка седловины являются характерными точками рельефа; линия водораздела хребта , линия водослива лощины, линия подошвы горы или хребта, линия бровки котловины или лощины являются характерными линиями рельефа.
Способы изображения рельефа. Способ изображения рельефа должен обеспечивать хорошее пространственное представление о рельефе местности, надежное определение направлений и крутизны скатов и отметок отдельных точек, решение различных инженерных задач.
За время существования геодезии было разработано несколько способов изображения рельефа на топографических картах. Перечислим некоторые из них.
Способ отмывки. Этот способ применяется на мелкомасштабных картах. Поверхность Земли показывается коричневым цветом: чем больше отметки, тем гуще цвет. Глубины моря показывают голубым или зеленым цветом: чем больше глубина, тем гуще цвет.
Способ отметок. При этом способе на карте подписывают отметки отдельных точек местности.
В настоящее время на топографических картах применяют способ горизонталей в сочетании со способом отметок, причем на одном квадратном дециметре карты подписывают, как правило, не менее пяти отметок точек.
Способ горизонталей. Сущность способа горизонталей можно понять из рис.5.6.
Мысленно рассечем участок местности горизонтальной плоскостью на высоте H. Линия пересечения этой плоскости с поверхностью Земли называется горизонталью. Горизонталь на местности — это замкнутая кривая линия, все точки которой имеют одинаковые отметки. Уменьшенное изображение на карте горизонтальной проекции горизонтали местности также называют горизонталью.
Для того, чтобы изобразить горизонталями рельеф участка местности, нужно рассечь его не одной, а несколькими горизонтальными плоскостями, расположенными на одинаковом расстоянии по высоте одна от другой. Это расстояние называется высотой сечения рельефа и обозначается буквой h. На местности горизонтали не пересекаются, так как они лежат в разных параллельных плоскостях; на карте они тоже как правило не пересекаются.
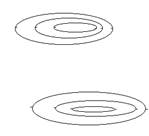
Все основные формы рельефа имеют свой рисунок горизонталей; при этом и гора и котловина изображаются системами замкнутых горизонталей (рис.5.7). Чтобы различить эти формы рельефа, а также для некоторых других целей на карте принято показывать направление скатов вниз; для этого применяются бергштрихи — короткие штрихи, перпендикулярные горизонталям и направленные по скату вниз.

Основные горизонтали имеют отметки, кратные высоте сечения рельефа h, начиная от нуля счета высот. Для выражения характерных особенностей рельефа рекомендуется проводить полугоризонтали и четвертьгоризонтали; они проводятся штриховыми линиями через половину и четверть сечения рельефа на отдельных участках карты (где расстояние между основными горизонталями слишком большое).
Каждая пятая основная горизонталь при h = 1, 2, 5, 10 м и каждая четвертая при h = 0.5 и 2.5 м утолщаются. Отметки некоторых горизонталей на карте подписывают, ориентируя основания цифр вниз по склону.
Крутизна и направление скатов. На рис.5.6 видно, что расстояние a между горизонталями на горизонтальной проекции участка зависит от крутизны ската. При одинаковой высоте сечения рельефа расстояние между горизонталями тем меньше, чем круче скат. Крутизна ската характеризуется углом наклона ν:
Тангенс угла наклона называется уклоном и обозначается буквой i; уклон обычно выражают в процентах или промилле (промилле — это тысячная часть целого).
Рассечем скат горы горизонтальными плоскостями при высоте сечения h (рис.5.8); на участке BC скат имеет угол наклона ν 1, на участке CD — угол наклона ν2. Расстояние a1 — это горизонтальное проложение линии ската BC; оно называется заложением.
Заложение, перпендикулярное к горизонталям, называется заложением ската, то-есть, заложение ската — это горизонтальная проекция линии наибольшей крутизны ската в данной точке; оно принимается за направление ската. Измерив на карте отрезок a и зная высоту сечения рельефа h, по формуле (5.4) можно вычислить тангенс угла наклона, а затем и сам угол наклона ν.
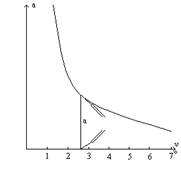
График заложений. Для быстрого определения угла наклона по карте пользуются специальным графиком, который называется графиком заложений. Он строится следующим образом (рис.5.9):
вычисляют заложение ската по заданной высоте сечения рельефа для разных углов наклона 0.5o, 1o, 2o и т.д.,
проводят прямую линию и откладывают на ней равные отрезки длины, которые подписывают в градусах угла наклона,
перпендикулярно этой линии откладывают в масштабе карты заложения ската, вычисленные для каждого значения угла наклона,
соединяют полученные точки плавной кривой.
Если теперь требуется определить угол наклона для конкретного заложения ската a, раствором циркуля, равным a, находят соответствующее место на графике и считывают угол наклона (на рис.4.9 ν = 4o 30′).
Аналогично можно построить график заложения для уклонов i.
График заложения помещается внизу листа карты справа.
Расчет высоты сечения рельефа. При проектировании работ по созданию карты или плана высоту сечения рельефа h выбирают в зависимости от масштаба карты, характера рельефа и назначения карты или плана. При этом условились изображать горизонталями скаты до 45o; скаты большей крутизны изображают специальным условным знаком обрыва. С другой стороны, расстояние между горизонталями на карте нельзя уменьшать до бесконечности, иначе они сольются. Считается, что наименьшее расстояние между горизонталями может быть 0.2 мм. При amin = 0.2 мм и νmax = 45o высоту сечения рельефа для конкретного масштаба можно подсчитать по формуле:
h = amin ∙ M ∙ tg(νmax). (5.5)
Например, для масштаба 1:M = 1:5 000 получим h = 1 м.
По формуле (5.5) находят так называемую расчетную высоту сечения рельефа. В зависимости от характера рельефа Инструкция [14] рекомендует для планов масштаба 1:5000 несколько значений высоты сечения рельефа:
для плоскоравнинной местности h = 0.5 м или h = 1 м,
для равнинной и всхолмленной местности h = 1 м или h = 2 м,
для горной местности h = 5 м.
Правильный выбор высоты сечения рельефа очень важен с экономической точки зрения, так как при уменьшении высоты сечения возрастает объем работ и расходы на производство съемки.
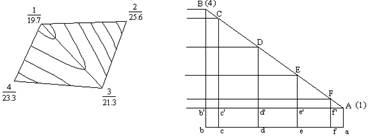
Проведение горизонталей по отметкам точек. Чтобы провести на карте (или плане) горизонтали, необходимо иметь точки с известными отметками, которые назовем пикетами. Пусть даны пикеты 1, 2, 3, 4 (рис.5.10), и предполагается, что вдоль линий 1-2, 1-3, 1-4, 2-3 и 3-4 местность имеет равномерный уклон. Требуется провести горизонтали внутри участка, ограниченного линиями 1-2, 2-3, 3-4, 4-5; высота сечения рельефа h= 1 м.
Процесс нахождения на линии, соединяющей два пикета, точек, через которые пройдут горизонтали, называется интерполированием горизонталей. Известны три способа интерполирования: аналитический, графический и на глаз.
Рассмотрим аналитический способ, являющийся основой для двух остальных способов. На рис.5.11 проведем линию местности, например, 4-1, и ее горизонтальную проекцию и затем покажем секущие плоскости, проходящие через 1 м по высоте. Обозначим точки линии 4-1 буквами A, F, E, D, C, B. Спроектируем эти точки пересечения секущих плоскостей с линией 4-1 на ее горизонтальную проекцию, получим точки a, f, e, d, c, b. Задача заключается в вычислении расстояний af, ae, ad, ac.
Из подобия треугольников FAf’ и BAb’ имеем:
af = Af’ = Ab’∙(HF — H1)/(H4 — H1).
Обозначим Ab’ через s и запишем окончательно:
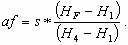
Если рис.5.11 построить в масштабе карты (плана), то отрезок s можно взять прямо с карты; отметки пикетов 1 и 4 известны, отметка точки F равна отметке первой секущей плоскости выше точки A.
Аналогично можно вычислить остальные отрезки. Отложив их на линии 4-1, получим на ней искомые точки.
На отрезках 1-2, 2-3 и других таким же образом найдем точки их пересечения с горизонталями. Затем плавными линиями соединим точки с одинаковыми отметками и получим рисунок горизонталей.
Аналитический способ применяют довольно редко ввиду его большой трудоемкости. Гораздо чаще применяют графический способ, при котором используется палетка (лист прозрачной бумаги или пластика), на котором проведены параллельные или расходящиеся прямые линии. Интерполирование на глаз применяют при небольших расстояниях между пикетами и при малых разностях отметок пикетов.
Источник