Способы измерения ускорения движения тела

Способы измерения ускорения движения тела

Новый Эталон Килограмма

может в ближайшее время заменить устаревший платиново-иридиевый. »»»

Солнце Становится Ближе

получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory. »»»

Человек «Искрививший» Время

биография Альберта Эйнштейна — величайшего физика создавшего «Общую теорию относительности». »»»

Что за Очки у Будущего?

история создания, развития и будущее популярного оптического прибора. »»»

Одним из способов определения скорости или ускорения движущегося тела является измерение через равные промежутки времени, отсчитанные секундомером или электронным тай­мером длины пути по траектории движения. Пройденное расстояние, поделенное на затраченное время,— это средняя скорость для каждого участка пути. Ускорение может быть вычислено по разности в скоростях, подсчитанных для двух различных участков на пути движения тела, де­ленной на временной интервал между этими двумя участками.

Другим способом определения ско­рости или ускорения является присо­единение телеграфной ленты к движу­щемуся телу. Движущееся тело про­тягивает ленту через телеграфный ап­парат — таймер, как показано на ри­сунке.

Магнитное поле катушки заставляет колебаться стальную по­лоску таймера с частотой 50 раз в се­кунду, которая оставляет черные точки на белой бумажной ленте, движущейся под копировальным диском. Каж­дая последующая пара точек пред­ставляет временной интервал 1/50 с (0,02 с) вне зависимости от того, на сколько будут отстоять эти точки друг от друга. Замеренное расстояние между любыми двумя последующими точками — это расстояние, которое прошло тело за 0,02 с. Поскольку лента фиксирует и пройденное рас­стояние, и затраченное на это время, го полученные данные позволяют подсчитать скорость.

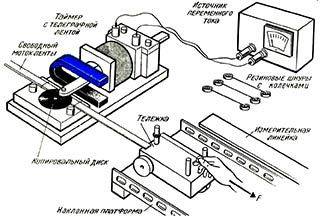
Можно составить своеобразную таблицу, если разрезать ленту на по­лоски и приклеить их на разграфлен­ную бумагу. Каждая полоска должна охватывать одинаковый временной ин­тервал, например десять отрезков представляют 0,2 с. Длина первой ленты — это расстояние, пройденное за 0,2 с, и, таким образом, средняя скорость на этом расстоянии определя­ется делением длины ленты на 0,2 с.

Источник

Измерение средней скорости движения тела определение ускорения движения тела

Лабораторная работа № 2.

Измерение средней скорости движения тела

Определение ускорения движения тела

Цель работы: – овладеть практическими навыками измерения скорости тела по величине его перемещения и времени движения;

– отработать практический прием определения ус­корения тела по его перемещению и времени движения.

Оборудование: секундомер, желоб, стальной шарик, металлический брусок, опора желоба, укладочный пенал.

1. Равномерное прямолинейное движение. Средняя скорость.

Рассматривая движение каких-либо тел, мы всегда отмечаем: на самолете добраться до нужного места можно гораздо быстрее, чем на поезде; автомобиль движется бы­стрее велосипедиста и т. п.

Движение различных тел происходит с разной быстро­той.

Для характеристики быстроты и направления движения тела служит векторная величина, называемая скоростью.

Равномерное прямолинейное движение – простейший вид механического движения, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Это движение с постоянной по модулю и направлению скоростью. При равномерном движении скорость показывает, какой путь прошло тело в единицу времени.

Обозначается скорость буквой V, а время движения буквой t. Таким образом, скорость тела при равномерном движении — это величина, равная отношению пути ко времени, за которое этот путь пройден:

или . (1)

В СИ за основную единицу скорости принят м/с (метр в секунду): [V]=[м/с]. Скорость равномерного движения, равная 1 м/с, показывает, что тело за 1 с проходит путь длиной в 1 м. [V]=[м/с] — это производная единица, ее получают согласно формуле скорости, подстав­ляя вместо физических величин, входящих в формулу, единицы их измерения.

Скорость имеет не только численное значение, но и направление. Это очень важно для определения местопо­ложения тела в определенный момент времени. Если из­вестно, что автомобиль был в пути 2 часа, двигаясь со скоростью 60 км/ч, то можно определить, что он проехал 120 км, но при этом вы не сможете сказать, где именно оказался автомобиль, так как не было указано направление движения. При указании направления становится возмож­ным зафиксировать положение движущегося тела в про­странстве. Скорость — это векторная величина. Зная ско­рость, можно найти перемещение S за любой промежуток времени t:

. (2)

Направление вектора скорости совпадает с направле­нием вектора перемещения. Направление вектора скорос­ти — это направление движения тела.

При вычислениях пользуются не самим вектором ско­рости, а его проекцией на ось. Проекции векторов — величины скалярные, поэтому с ними можно производить алгебраические действия.

В случае неравномерного (переменного) движения разли­чают мгновенную и среднюю скорости. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным движением.

На рис. 1 показаны положения санок, ко­торые сначала скатываются по наклонной плоскости (ледяной по­верхности горки), а затем движутся по горизонтальному участку, через равные промежутки времени. Сравнивая перемещения санок за одинаковые промежутки времени, видим, что при скатывании са­нок с ледяной горки расстояние между ними увеличивается, следо­вательно, скорость санок возрастает. Скатившись с горки, санки по­степенно замедляют свое движение — за равные промежутки време­ни уменьшается расстояние, пройденное санками.

При неравномерном движении тело совершает за одинаковые промежутки времени неодинаковые перемещения. Скорость такого перемещения изменяется от точки к точке траектории движения. Для характеристики переменного (неравномерного) движения пользу­ются понятием средней скорости. Для нахождения средней скоро­сти на данном участке пути (или за данное время) надо пройден­ный телом путь разделить на время его движения:

или . (3)

Если тело проходит участки пути …, соответственно за время …, , то средняя скорость

. (4)

Например, добираясь до школы, вы пользуетесь трол­лейбусом, метро, а часть пути проходите пешком. Чтобы подсчитать среднюю скорость вашего движения (на данном участке пути или за данный промежуток времени), нужно знать, сколько времени вы затрачиваете на каждом этапе движения, и путь, который соответствует каждому участку движения.

Предположим, пешком до остановки троллейбуса вы проходите 300 м и затрачиваете на этот путь 240 с, на троллейбусе вы проезжаете 2000 м и затрачиваете 360 с, на метро путь равен 6000 м, а время — 600 с. Ну а до магазина,

выйдя из метро, вы проходите 100 м за 80 с.

В таком случае средняя скорость вашего движения на протяжении всей дороги в школу определяется как:

.

Но запомните: нельзя пользоваться средними значе­ниями скоростей для нахождения средней скорости мето­дом среднего арифметического!

Например, средняя скорость пешехода (в нашем слу­чае) ≈1,3 м/с, поезд метро имеет скорость 36 км/ч, что соответствует ≈10 м/с, скорость троллейбуса ≈20 км/ч, что соответствует ≈5,5 м/с. Однако Vcp на всем участке пути — 6.6 м/с, а не 4.5, что могло бы получиться при подсчете Vcp методом среднего арифметического:

Итак, этот метод неприменим, ибо не соответствует определению скорости как физической величины. Кроме того, вы должны обратить внимание на то, что числовое значение одной и той же скорости в разных единицах измерения различно. Это зависит от выбора единицы из­мерения (36 км/ч и 10 м/с).

Чаще всего скорость выражается именно в км/ч, но существующая Международная система единиц требует умения переводить скорость из км/ч в м/с и обратно.

Для этого нужно запомнить, что для перевода км/ч в м/с данную величину скорости нужно домножить на 1000 (так как в 1 км — 1000 м) и разделить на 3600 (в 1 ч — 3600с).

Можно также запомнить, что 36 км/ч=10 м/с и в дальнейшем оценивать значение скорости в других едини­цах на основе пропорциональности.

Например, 72 км/ч=20 м/с; 54 км/ч=15 м/с и т. п.

Мгновенная скорость — это скорость в данной точке траектории в данный момент времени. Мгновенной скоростью называют предел, к которому стремится средняя скорость за бесконечно малый промежуток времени:

(5)

Скорость равномерного прямолинейного движения тела является его мгновенной скоростью, так как она одинакова в любой момент времени и в любой точке траектории.

2. Неравномерное движение.

Движение любого тела в ре­альных условиях никогда не бы­вает строго равномерным и пря­молинейным. Движение, при ко­тором тело за равные промежут­ки времени совершает неодинако­вые перемещения, называют не­равномерным движением.

При неравномер­ном поступательном движении скорость тела изменяется с тече­нием времени. Процесс измене­ния скорости тела характеризу­ется ускорением.

Физическая величина, характеризующая быстроту изменения скорости и равная отношению изменения скорости к промежутку времени , за которое произошло это изменение, называется средним ускорением:

(6)

Если за промежуток времени тело из точки А траектории переместилось в точку В и его ско­рость изменилась от до , то изменение скорости за этот промежуток времени равно разно­сти векторов и : =—.

Направление вектора ускоре­ния совпадает с направлением вектора изменения скорости при очень малых значениях про­межутка времени , за который происходит изменение скорости.

Если тело движется прямоли­нейно и скорость его возрастает по модулю, т. е. >, то на­правление вектора ускорения совпадает с направлением векто­ра скорости (рис. 2); при убы­вании скорости по модулю, т. е. при >, направление вектора ускорения противоположно на­правлению вектора скорости (рис. 3).

При движении тела по криво­линейной траектории направле­ние вектора скорости изменяется в процессе движения, вектор уско­рения при этом может оказаться направлен под любым углом к вектору скорости (рис. 4).

Рис. 2. Рис. 3. Рис. 4.

Самый простой вид неравномерного движения – это равноускоренное движение. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:

(7)

Из формулы следует, что при выражении скорости в метрах в секунду, а времени в секундах ускорение выражается в метрах на секунду в квадрате:

Прямолинейное движение с постоянным ускорением, при котором
модуль скорости увеличивается, называется равноускоренным движением, а прямолинейное движение с постоянным ускорением, при котором модуль скорости уменьшается, называется равнозамедленным.

Пусть — скорость точки в начальный момент времени , а — её скорость в любой момент времени t. Тогда , =—, и формула для ускорения примет вид

Если начальный момент времени принять равным нулю, то получим

(8)

Векторному уравнению (8) соответствуют в случае движения на плоскости два уравнения для проекций скорости на координатные оси Ox и Oy:

(9)

При движении с постоянным ускорением скорость со временем меняется по линейному закону.

Перемещение тела при равноускоренном прямолинейном движении описывается векторным уравнением:

(10)

Тогда уравнение для координаты точки при равноускоренном движении имеет вид (в проекции на ось Ox):

(11)

Где -координата тела в начальный момент.

При равноускоренном движении проекция перемещения тела связана с конечной скоростью следующей формулой:

(12)

Если начальная координата равна нулю и начальная скорость также равна нулю, то формулы (9), (11) и (12) примут следующий вид:

(13)

(14)

(15).

1 часть. В работе надо определить среднюю скорость стального шарика, скатывающегося по наклонному желобу. Для этого необходимо найти отношение перемещения, совершенное телом ко времени, за которое оно совершено.

2 часть. Измерить ускорение шарика, с которым он движется по поверхности наклонного желоба из состояния покоя (начальная скорость шарика равна нулю). Из урав­нения для равноускоренного прямолинейного движения следует, что в этом случае перемещение шарика, ускорение и время движе­ния связаны соотношением: S=at2/2, откуда a=2S/ t2. Следовательно, чтобы определить ускорение, достаточно изме­рить перемещение и время, затраченное на это перемещение.

Перемещение определяют по разности конечной и начальной координат шарика. Время движения — секундомером.

1. Соберите экспериментальную установку.

Основу экспериментальной установки составляет прямой же­лоб, один конец которого закреплен несколько выше другого. Его кладут на крышку укладочного модуля. Под один его конец подкладывают опору и регулируют его положения так, чтобы верхний конец желоба оказался выше на 3 — 4 мм. Общий вид установки показан на рисунке 5.

Объектом наблю­дения в работе являет­ся стальной шарик. Установку можно счи­тать окончательно на­строенной, если ша­рик скатывается от края до края желоба за 4-5 секунд.

Для определения координаты шарика используют брусок и внутреннюю шкалу на поверхности желоба. Брусок кладут в желоб на пути движения шарика. Шарик, скатываясь по желобу, ударит­ся о брусок. Координату шарика определяют по положению гра­ни бруска, которой он коснется в момент удара.

Работу начинают с определения начальной координаты шари­ка. В 2 — 3 см от верхнего края на желоб устанавливают брусок и шарик. Шарик должен располагаться выше бруска. Начальную координату () определяют по положению точки соприкосновения ша­рика и бруска. Для этого достаточно заметить деление шкалы, ря­дом с которым находится основание бруска, которого касается ша­рик. Затем заносят значение в таблицу 1.

Определив начальную координату, шарик удерживают рукой в исходном положении, а брусок смещают вниз по по­верхности желоба. По основанию бруска, о которое ударится ша­рик, определяют конечную координату шарика (), которую он будет иметь, пройдя путь вдоль желоба. Значение также заносят в таблицу 1. Определив координаты начальной и конечной точки движе­ния, вычисляют его перемещение. Перемещение шарика (S) определяют по разности конечной и на­чальной координаты:

(16)

Значение перемещения заносят в таблицу 1.

Затем шарик отпускают и одновременно включают секундомер. По звуку удара шарика о брусок секундо­мер останавливают и считывают его показания, которые заносят в таблицу 1. Таким образом, мы определили время движения шарика t.

Для исключения случайных по­грешностей проводят 5 пусков при тех же начальных и конечных координатах. (То есть перемещение остается одинаковым.). При этом время движения шарика будет различным (вы можете чуть раньше или чуть позже включать (выключать) секундомер). Все данные записываются в таблицу 1.

Далее вычисляют среднее время движения шарика:

(17)

После чего вычисляют среднюю скорость движения шарика:

(18)

По полученным данным определяют ускорение шарика:

(19)

Результаты всех измерений и вычислений записывают в таблицу 1.

Источник