Способы измерения угловой скорости

Все об угловой скорости — определение, единица измерения, методы расчета

Что такое угловая скорость

​Угловая скорость (обозначается как \(\omega\) ) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.

Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.

Единица измерения

В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула угловой скорости

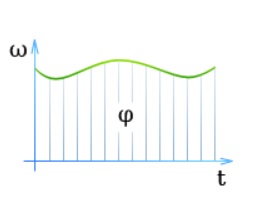
Вектор угловой скорости определяется отношением угла поворота \((\varphi)\) к интервалу времени \((\mathcal t)\) , за которое произошел поворот:

Зависимость угловой скорости от времени

Зависимость \(\varphi \) от \(\mathcal t\) наглядно показана на графике:

Угол, на который повернулось тело, характеризуется площадью под кривой.

Угловая скорость вращения, формула

Через частоту

\(\mathcal n\) — частота вращения \((1/с)\)

\(\pi\) — число Пи ( \(\approx 3,14\) )

\(T \) — период вращения (время, за которое тело совершает один оборот)

Через радиус

\(v\) — линейная скорость(м/с)

\(R\) — радиус окружности (м)

Как определить направление угловой скорости

Направление скорости в физике можно определять двумя способами:

1. Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
2. Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.

Связь линейной и угловой скорости

Линейная скорость \((v)\) тела, расположенного на расстоянии \(R\) от оси вращения, прямо пропорциональна угловой скорости.

\(R\) — радиус окружности (м)

Чему равна мгновенная угловая скорость

Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при \(\triangle\mathcal t\rightarrow0\) :

Источник

МЕТОДЫ ИЗМЕРЕНИЯ УГЛОВОЙ СКОРОСТИ ВРАЩЕНИЯ ВАЛА

Рассмотрим следующие методы измерения угловой скорости вращения вала: центробежный, часовой, фрикционный, магнит­ный, индукционный, импульсный, стробоскопический и метод дифференцирования.

1. Центробежный метод [1]

Центробежный метод основан на зависимости центробежных сил от угловой скорости вращения инерционной массы.

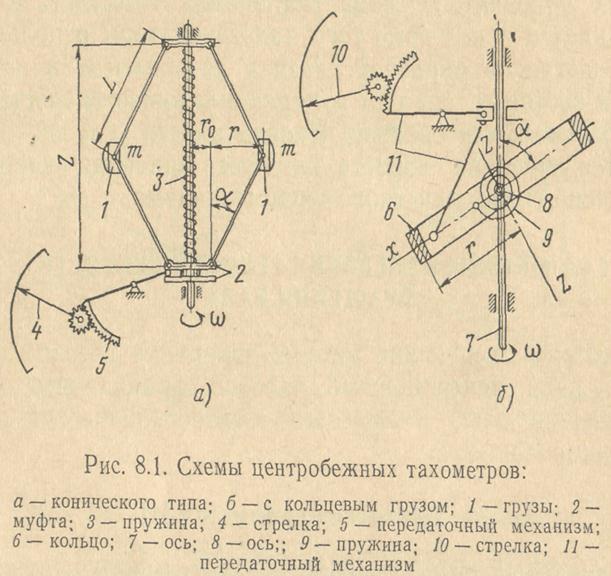
Существуют две типовые схемы центробежных тахометров — тахометр конического типа и с кольцевым грузом.

В тахометре конического типа на вращающейся оси при по­мощи шарниров прикреплено несколько грузов (два, три или че­тыре), которые при наличии угловой скорости развивают центро­бежные силы и симметрично расходятся, перемещая вдоль оси муфту и сжимая пружину до тех пор, пока ее упругая сила не уравновесит центробежные силы (рис. 8.1, а).

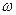
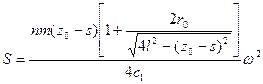
Зависимость перемещения s муфты от угловой скорости вы­ражается формулой [1]

,

где n – число грузов,

m – масса одного груза,

с₁ – коэффициент линейной жесткости пружины,

z₀ – длина пружины в свободном состоянии,

r₀ и l – размеры, обозначенные на рис. 8.1.

Для малых перемещений можно пренебречь величиной s по сравнению с z₀ и тогда

.

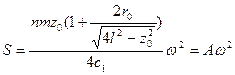
Из выражения (8.2) следует, что центробежный тахометр обладает квадратичной характеристикой.

Схема центробежного тахометра с кольцевым грузом изобра­жена рис. 8.1, б. На оси, связанной с контролируемым валом, по­мещен кольцевой груз, имеющий дополнительную степень свобо­ды относительно поперечной оси, вращающейся вместе с основ­ной осью. Когда кольцевой груз расположен под некоторым углом, а к основной оси (см. рис. 8.1, б), возникающие при его вра­щении инерционные силы создают вращающий момент М_вр отно­сительно поперечной оси и стремятся повернуть кольцо так, что­бы его плоскость была перпендикулярна оси вращения. Враща­ющему моменту М_вр противодействует момент М_пр спиральной пружины; равновесие наступает при равенстве М_пр = М_вр, чему соответствует некоторый угол .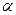

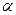
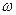
Зависимость угла от угловой скорости для тахометра с кольцевым грузом также является квадратичной.

В динамическом отношении чувствительный элемент тахомет­ра с кольцевым грузом, так же как и тахометра конического ти­па, в случае применения воздушного демпфера является колеба­тельным звеном 3-го порядка (см.стр. 54).

2. Часовой метод [3]

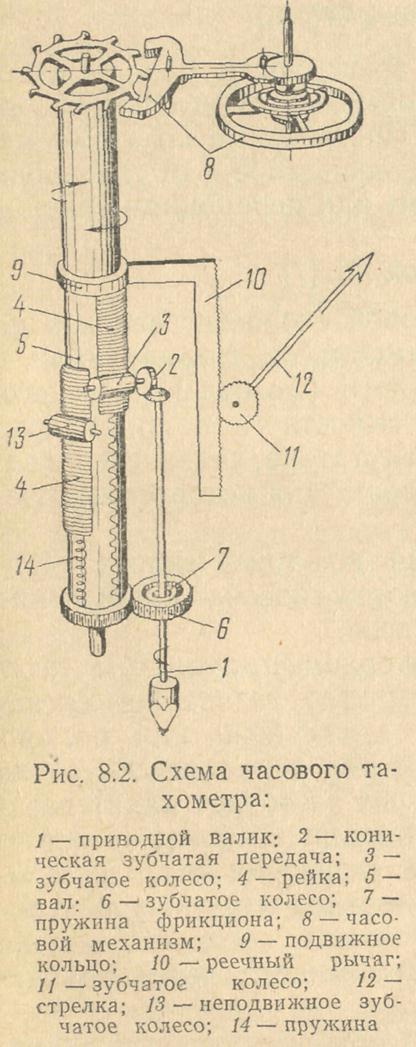
Часовой метод измерения угловой скорости основан на зави­симости угла поворота вала за фиксированный промежуток вре­мени от угловой скорости его вращения.

В часовых тахометрах временной интервал задается с помо­щью часового механизма, а величина накопленного за этот про­межуток времени угла поворота вала передается на указываю­щую стрелку (рис. 8.2).

Часовые тахометры имеют линей­ную характеристику, их особен­ность — дискретность измерения (определение результата за конт­рольный интервал времени).

3. Фрикционный метод [3]

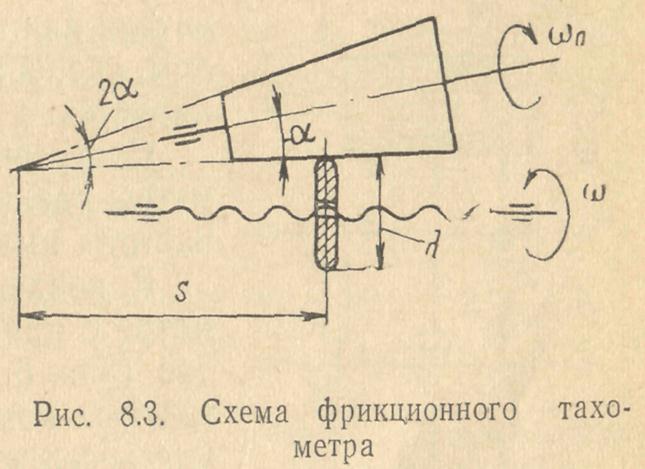
Фрикционный метод измерения угловой скорости основан на само­выравнивании (за счет трения

скольжения) окружной скорости вращения фрикционного ролика с окружной скоростью конуса, вра­щающегося с постоянной угловой скоростью 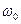. Мерой измеряемой

угловой скорости 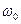является величина s расстояния ролика от

вершины конуса (рис. 8. 3):

,

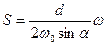
где d – диаметр ролика,

— угол конуса.

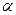
4. Магнитоиндукционный метод [1]

Магнитоиндукционныи метод основан на увлечении проводя­щего тела (цилиндра, диска и др.) полем вращающегося посто­янного магнита благодаря взаимодействию наводимых в прово­дящем теле индукционных токов с магнитным полем постоянного магнита.

Построенные по этому методу магнитоиндукционные (магнит­ные) тахометры подробно рассматриваются в § 8.3.

5. Индукционныйметод [4], [5]

Индукционный метод основан на зависимости э. д. с, наво­димой полем постоянного магнита в обмотке, от угловой скоро­сти вращения магнита или обмотки. Построенные по этому ме­тоду тахогенераторы описаны в § 8.4; в зависимости от схемы они могут выдавать сигналы на постоянном или переменном токе.

6. Импульсный метод[2], [7]

Импульсный метод измерения угловой скорости основан на определении частоты электрических импульсов, формируемых с помощью контактного или бесконтактного (фотоэлектрического,

индуктивного, емкостного и др.) преры­вателя или коммутатора, связанного с ва­лом, скорость вращения которого контро­лируется.

Построенные по этому методу тахометры различаются способами измерения частоты импульсов.

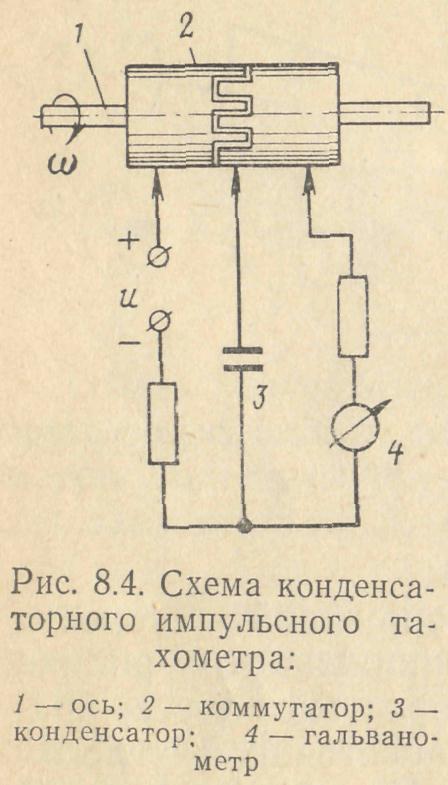
В конденсаторном импульсном тахо­метре с прямым преобразованием сигна­лов (рис. 8.4) контактный или бескон­тактный коммутатор периодически (один или несколько раз за оборот вала) пере­ключает конденсатор на заряд от источ­ника питания и на разряд через измери­тель тока (гальванометр). Мерой угло­вой скорости служит среднее значение силы тока, протекающего через гальва­нометр.

В конденсаторном импульсном тахо­метре компенсационного типа среднее

значение напряжения, создающегося на конденсаторе при его периодической коммутации, уравновешивается (автоматически) с помощью самобалансирующейся мостовой схемы со сле­дящим электроприводом.

Для повышения точности измерения используются стабильные слюдяные конденсаторы с температурным коэффициентом емко­сти не более 50• 10 -6 на 1 0 С.

В импульсных тахометрах в качестве коммутатора может быть использован тахогенератор переменного тока с вращающим­ся магнитом; синусоидальное напряжение, выдаваемое тахогенератором, используется для управления полупроводниковыми ключами.

7. Стробоскопический метод [6]

Стробоскопический метод основан на явлении кажущейся не­подвижности вращающегося тела при его периодическом наблю­дении в течение коротких промежутков времени с частотой, рав­ной или кратной частоте вращения (числу оборотов за 1 сек).

Различают стробоскопы с механическим затвором, через кото­рый наблюдается вращающееся тело, с механическим обтюрато­ром, прерывающим луч света, освещающий вращающееся тело, и с электронной схемой, управляющей частотой вспышек осве­тительной газонаполненной лампы, освещающей вращающееся тело.

8. Метод дифференцирования

Метод дифференцирования основан на дифференцировании сигнала позиционного датчика (потенциометрического, индуктив­ного или др.).

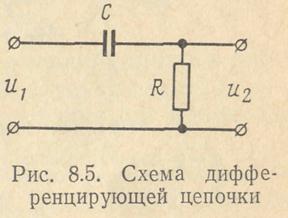
Метод применим при ограниченной величине углового пере­мещения контролируемого вала; примером простейшей схемы яв­ляется пассивная цепочка R—С (рис. 8.5), дифференцирующая напряжение

постоянного тока, снимаемое с потенциометра.

Передаточная функция такого дифференциатора

,

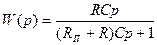
где R_n — внутреннее сопротивление по­тенциометра.

Для построения дистанционных тахометров на летательных аппаратах используется в основном магнитоиндукционный метод благодаря его простоте и линейной зависимости показания при­бора от угловой скорости.

В качестве датчиков систем автоматического управления и следящих систем используются тахогенераторы постоянного и переменного тока, основанные на индукционном методе.

В устройствах с ограниченной величиной перемещения вала применяют иногда схемы электрического дифференцирования.

Определенную перспективу имеют импульсные методы, осо­бенно в связи с развитием цифровых вычислительных машин.

Центробежный, часовой, фрикционный и стробоскопический методы измерения угловой скорости вращения вала не получили развития на летательных аппаратах по тем или другим причи­нам (громоздкость, неудобства монтажа, трудность автоматиза­ции измерений, нелинейность характеристик, увеличенные погреш­ности и т. п.).

Рассмотрим более подробно магнитоиндукционные тахомет­ры и тахогенераторы.

§ 8.3. МАГНИТОИНДУКЦИОННЫЕ ТАХОМЕТРЫ 1. Схемы и характеристики магнитоиндукционных тахометров

Применяются два варианта магнитоиндукционных тахомет­ров — с цилиндрическим чувствительным элементом и с дисковым (рис. 8.6).

В первом варианте (см. рис. 8.6, а) на вращающейся оси ук­реплена магнитная система, состоящая из постоянного магнита с одной, двумя или тремя парами полюсов и кольцевого экрана из мягкого железа, через который замыкается магнитный поток магнита.

В кольцевом воздушном зазоре между магнитом и экраном расположен тонкостенный токопроводящий цилиндр, укреплен­ный на отдельной оси, соосной с осью магнитной системы. Ось цилиндра несет на себе также указывающую стрелку и связана со- спиральной противодействующей пружиной.

При вращении магнитной системы с угловой скоростью а в токопроводящем цилиндре наводится электродвижущая сила е, вызывающая ток I, замыкающийся в теле цилиндра; в результате взаимодействия тока i с магнитным полем постоянного магнита создается движущий момент М_яв, стремящийся увлечь цилиндр вслед за вращающейся магнитной системой; этому препятствует пружина, развивающая противодействующий момент М_пр. В ре­зультате подвижная система (цилиндр вместе с указывающей стрелкой) поворачивается на некоторый угол 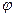, величина кото­рого определяется равновесием моментов М_пр = М_дв.

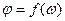
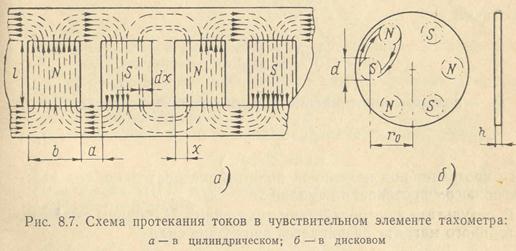
Зависимость является статической характеристикой (уравнением шкалы) прибора. Для определения этой зависимо­сти рассмотрим картину протекания индукционных токов на схе­ме на рис. 8.7, а, где изображена поверхность цилиндра, развер­нутая в виде токопроводящей ленты.

Будем считать магнитную систему неподвижной, а ленту — движущейся с линейной скоростью 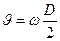—, где D — диаметр ци­линдра.

Магнитный поток пронизывает ленту перпендикулярно к пло­скости чертежа; области, внутри которых действует поток, огра­ничены на схеме прямоугольниками, изображающими проекции полюсов постоянного магнита на поверхность ленты.

Выделим в ленте над поверхностью полюса, на расстоянии х от его края, узкую полоску шириной dx и толщиной 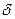, равной толщине стенки цилиндра.

При движении ленты со скоростью v в полоске будет наво­диться э. д. с.

,

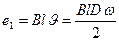
где В — магнитная индукция в рабочем зазоре;

l — длина полюса постоянного магнита.

Поскольку магнитный поток над соседним полюсом имеет противоположное направление, то э. д. с, наводимая в анало­гичной полоске, расположенной на расстоянии х от края сосед­него полюса, будет такой же величины, т. е. е₂=е₁.

В итоге под действием э. д. с. е₁ и е₂ образуется короткозамкнутый элементарный виток тока

.

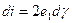
Источник