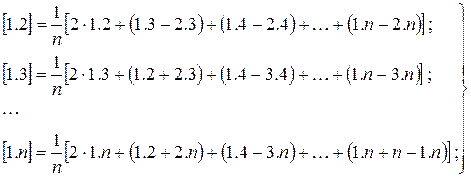Способы измерения углов с точностью

Измерение горизонтальных углов. Точность измерений

Работа по измерению углов на станции выполняется в следующем порядке:

— установка теодолита в рабочее положение;

— измерение горизонтальных углов (направлений);

— обработка журнала наблюдений и контроль измерений.

Для установки теодолита в рабочее положение нужно выполнить три действия:

1 Ц е н т р и р о в а н и е. Центрирование, или установку оси вращения прибора над вершиной угла выполняют с помощью отвеса (нитяного или оптического) путем перемещения теодолита и штатива до тех пор, пока острие грузика отвеса или пересечение сетки нитей оптического отвеса не установится над вершиной угла.

2 Г о р и з о н т и р о в а н и е. Горизонтирование, или приведение оси вращения прибора в отвесное положение, выполняют следующим образом. Устанавливают уровень при алидаде горизонтального круга по направлению двух подъемных винтов и, действуя ими, приводят пузырек уровня в нуль-пункт. Затем поворачивают алидаду на 90 о , располагая ось уровня по направлению третьего подъемного винта. Вращая этот винт, вновь приводим пузырек уровня в нуль-пункт. Эти действия повторяют до тех пор, пока при повороте алидады пузырек уровня не будет отклоняться более чем на одно деление.

3 У с т а н о в к а з р и т е л ь н о й т р у б ы д л я н а б л ю д е н и й. Состоит в установке трубы по глазу и предмету. Установку трубы по глазу осуществляют вращением окулярной трубочки до тех пор, пока штрихи сетки нитей не будут видны четко. Установку трубы по предмету осуществляют вращением кремальеры (у теодолита Т-30) или фокусировочного кольца трубы (у теодолитов Т5, Т2 и т. д.) до тех пор, пока изображение предмета не получится четким.

Для измерения горизонтальных углов наиболее часто применяются способ приемов (для измерения одного угла) и способ круговых приемов (при измерении углов на станции между тремя направлениями и более).

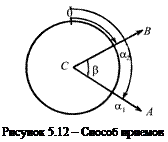
С п о с о б п р и е м о в. Для измерения угла АСВ (рисунок 5.12) теодолит устанавливают над вершиной угла С, приводят его в рабочее положение и закрепив лимб, вращением алидады наводят трубу на правую точку А. Закрепив алидаду, производят отсчет а₁ по горизонтальному кругу, например а₁ = 119 о 42′. Затем открепляют алидаду, визируют на левую точку В и делают отсчет а₂, например, а₂ = 57 о 14′. Величина измеряемого угла

β = а₁ – а₂ = 119 о 42′ – 57 о 14′ = 62 о 28′.

Если отсчет на точку А меньше отсчета на точку В, то его увеличивают на 360 о .

Такие действия по измерению угла называют первым полуприемом. Первый полуприем обычно выполняют при круге лево (КЛ).

Для контроля, ослабления влияния систематических погрешностей прибора и повышения точности угол измеряют при втором положении вертикального круга (КП), сместив лимб на 3–5 о . Для выполнения второго полуприема переводят трубу через зенит и, открепив закрепительный винт лимба, поворачивают его на 180 о . Измерение угла производят так же, как и в первом полуприеме. По полученным отсчетам вторично вычисляют величину угла. Расхождение значений углов между полуприемами не должно превышать двойной точности отсчета теодолита.

Два полуприема составляют один полный прием. За окончательный результат принимают среднее арифметическое из двух значений. Для повышения точности угол можно измерять несколькими приемами с перестановкой лимба между приемами на угол 180 о /n, где n число приемов.

С п о с о б к р у г о в ы х п р и е м о в. Этот способ применяют в тех случаях, когда необходимо измерить ряд углов при одной вершине. Пусть требуется измерить углы при точке А (рисунок 5.13). Для этого теодолит устанавливают в точке А и приводят его в рабочее положение. Затем, вращая алидаду по ходу часовой стрелки при закрепленном лимбе, последовательно визируют на все точки по заданным направлениям и берут отсчеты. Последнее наведение делают на начальное направление, чтобы убедиться в неподвиж-

ности лимба. Эти действия составляют первый полуприем (например, при круге лево).

Во втором полуприеме (при круге право) переводят трубу через зенит и последовательно визируют на все направления, но в обратном порядке – против хода часовой стрелки.

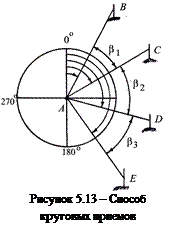
По результатам наблюдений вычисляют средние значения отсчетов по направлениям, как среднее арифметическое отсчетов при круге лево и круге право. По средним значениям направлений можно вычислить любой угол как разность соответствующих направлений его сторон. Например, согласно рисунку 5.13,

β₁ = AC – AB; β₂ = AD – AC и т. д.

В зависимости от требуемой точности углы измеряют различным числом приемов. Между приемами лимб переставляют на 180 о /n, где n – число приемов. Способ круговых приемов применяется в сетях триангуляции и полигонометрии 2-го класса и ниже, а также при развитии специальных геодезических сетей.

Т о ч н о с т ь и з м е р е н и я г о р и з о н т а л ь н ы х у г л о в. На точность измерения горизонтальных углов оказывают влияние следующие погрешности:

1) центрирования (зависит от неточности установки теодолита над точкой и длины стороны);

2) редукции (возникает из-за неточной установки визирных целей над точками);

3) визирования (зависит от точности наведения зрительной трубы на визирную цель и от увеличения зрительной трубы);

4) снятия отсчета (зависит от цены деления шкалы отсчетного устройства).

Совместное влияние перечисленных погрешностей не должно превышать двойной точности отсчетного устройства теодолита, если при измерениях не было грубых просчетов.

Источник

Способы угловых измерений

Результаты угловых измерений в ГГС должны быть равноточными, т.е. на всех пунктах иметь один и тот же вес, и получены с наивысшей точностью при наименьших затратах труда и времени. Для этого высокоточные измерения каждого направления и угла выполняют по строго одинаковой наиболее совершенной методике в периоды наивыгоднейшего времени наблюдений, когда влияние внешней среды минимально. Необходимо, чтобы каждое направление измерялось на разных диаметрах лимба, равномерно распределенных по кольцу делений; в приеме должно быть обеспечено единообразие операций при измерении каждого направления и симметрия во времени относительно среднего для приема времени наблюдений; целесообразно все направления и углы на пункте измерять симметрично относительно момента изотермии воздуха.

Перед выполнением наблюдений на пункте производят осмотр геодезического знака, откапывают центр до марки с меткой, на площадку наблюдателя поднимают теодолит и другое снаряжение, крышу сигнала накрывают брезентом. В результате осмотра наблюдатель должен убедиться в прочности и устойчивости столика сигнала и в том, что внутренняя пирамида не соприкасается с полом площадки для наблюдателя и с лестницей. Обнаруженные недостатки необходимо устранить.

Перед наблюдением с помощью теодолита согласно схеме геодезической сети отыскивают все подлежащие наблюдению пункты и после наведения на них делают с точностью до 1’ отсчеты по горизонтальному и вертикальному кругам. Кроме того, при наведении на пункты положение алидады фиксируют на нижней части прибора с помощью штрихов против индекса на алидаде. Теодолит устанавливают на штатив или столик сигнала не менее чем за 40 минут до начала наблюдений. К измерению горизонтальных направлений приступают при хорошей видимости, когда изображения визирных целей спокойны или слегка колеблются (в пределах 2”).

Измерение отдельного угла.Незакрепленную алидаду отводят влево на 30 – 40 0 и обратным вращением наводят на визирную цель первого направления так, чтобы она оказалась справа от биссектора, алидаду закрепляют. Наводящим винтом алидады, только ввинчиванием, биссектор наводят на визирную цель и берут отсчет по оптическому микрометру (если имеется окулярный микрометр, то трижды наводят его биссектор на визирную цель и берут отсчеты). Открепляют алидаду и наводят на 2-е направление так же, как и на 1-е. На этом заканчивается полуприем.

Трубу переводят через зенит, по часовой стрелке наводят на 2-е направление, предварительно отведя алидаду на 30 – 40 0 ; наводящим винтом биссектор наводят на визирную цель и берут отсчет по оптическому микрометру. По часовой стрелке алидаду поворачивают на угол, дополняющий измеряемый до 360 0 , наводят на визирную цель 1-го направления, берут отчет. Заканчивается прием.

Способ круговых приемов – способ Струве.Способ был предложен в 1816 г. В.Я. Струве, получил широкое применение почти во всех странах. В нашей стране используется в геодезических сетях 2 — 4 классов и сетях более низкой точности.

В этом способе при неподвижном лимбе алидаду вращают по ходу часовой стрелки и биссектор сетки нитей трубы последовательно наводят на первый, второй,…, последний и снова на первый (замыкание горизонта) наблюдаемые пункты, каждый раз отсчитывая по горизонтальному кругу. В этом состоит первый полуприем. Затем трубу переводят через зенит и, вращая алидаду против часовой стрелки, наводят биссектор на те же пункты, но в обратной последовательности: на первый, последний, …, второй, первый; заканчивают второй полуприем и первый прием., состоящий из первого и второго полуприемов.

Между приемами лимб переставляется на угол

,

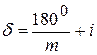
где m – число приемов, i – цена деления лимба.

Наведение биссектора на на визирную цель выполняют только ввинчиванием наводящего винта алидады. Перед каждым полуприемом алидаду вращают по ее движению в данном полуприеме.

В результаты измеренных направлений вводят поправки за рен, наклон вертикальной оси теодолита (при углах наклона визирного луча в 1 0 и более) и поправки за кручение знака – по отсчетам по окулярному микрометру поверительной трубы.

Контроль угловых измерений: по расхождениям значений первого направления в начале и конце полуприема (незамыкание горизонта), по колебанию двойной коллимационной ошибке, определяемой для каждого направления, и по расхождению приведенных к нулю значений одноименных направлений, полученных в разных приемах. В триангуляции 2 – 4 классов незамыкание горизонта и колебание направлений в приемах не должны превышать 5, 6 и 8” для Т05, Т1; ОТ-02 и Т2; колебание 2С – 6,8 и 12” для этих же теодолитов соответственно.

В пунктах 2 класса направления измеряют 12-15 круговыми приемами, на пунктах 3 класса – 9, на пунктах 4 класса – 6, а в сетях полигонометрии 2, 3, 4 классов – 18, 12, 9 приемами.

Уравнивание на станции сводится к вычислению среднего значения по каждому направлению из m приемов. При этом предварительно все измеренные направления приводят к начальному, придав ему значение 0 0 00’00,00”. Вес уравненного направления равен p = m – числу приемов измерений. Для оценки точности направления обычно применяют приближенную формулу Петерса

,

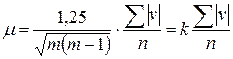
где μ – с.к.о. направления, полученного из одного приема (с.к.о. единицы веса); ∑‌‌[v] – сумма абсолютных величин уклонений измеренных направлений от их средних значений, вычисленных по всем направлениям; n, m – число направлений и приемов соответственно. Значения k при m = 6, 9, 12, 15 равны 0,23; 0,15; 0,11; 0,08. С.к.о. уравненного направления (среднего из m приемов) вычисляют по формуле

.

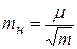
Достоинстваспособа круговых приемов: простота программы измерений на станции; значительное ослабление систематических ошибок делений лимба; высокая эффективность при хорошей видимости по всем направлениям.

Недостатки:сравнительно большая продолжительность приема, особенно при большом числе направлений; повышенные требования к качеству геодезических сигналов; необходимость примерно одинаковой видимости по всем направлениям; разбивка направлений на группы при их большом числе на пункте; более высокая точность начального направления.

Способ измерения углов во всех направлениях – способ Шрейбера.Этот метод предложен Гауссом. Методика разработана Шрейбером, применившим его в 1870-х годах в прусской триангуляции. В России начал применяться с 1910 г., используется и в настоящее время. Суть способа: на пункте с n направлениями измеряют все углы, образующиеся при сочетании из n по 2, т.е.

Число таких углов

.

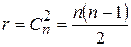
Значение углов можно получить путем непосредственных измерений и путем вычислений. Если вес непосредственно измеренного угла равен 2 , то вес этого же угла, полученного из вычислений, будет равен 1. Следовательно. Вес угла, полученного из вычислений, в два раза меньше веса непосредственно измеренного угла.

При уравнивании на станции для каждого угла вычисляют его среднее значение из всех приемов (при допустимых расхождениях между приемами). Используя эти средние, находят уравненные на станции углы как среднее весовое значение. Учитывая, что сумма весов измеренного и вычисленных значений данного угла 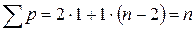, находим

где n – число направлений на пункте. Углы, полученные в результате уравнивания на станции, по направлениям – равноточны.

Применяя формулу веса функции, для угла [1.2] находим

.

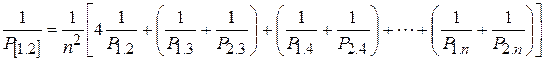
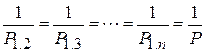
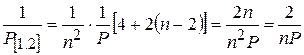
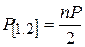
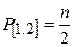
Так как , то , откуда . При Р = 1 , , т.е. веса уравненных углов равны половине числа направлений, наблюдаемых с данного пункта. Если каждый угол измерен m приемами, то при n направлениях вес каждого угла будет равен mn / 2. Для равенства весов окончательных углов на всех станциях необходимо, чтобы произведение mn для всех пунктов сети являлось постоянным. Так как вес направления в два раза больше веса угла, то mn – вес направления.

Вес углов, измеренных во всех комбинациях должен быть равен весу углов, измеренных способом круговых приемов, т.е. p = m_кр = mn / 2 , откуда 2m_кр = mn , где m_кр – число приемов в методе круговых приемов. Например, если углы в триангуляции 2 класса измеряют 15 круговыми приемами (m_кр = 15), то mn = 30; при числе направлений n = 5 способом во всех комбинациях их нужно измерять 6 приемами (m = 30 / 5 = 6).

При измерении углов способом во всех комбинациях выполняют следующий контроль: 1) расхождение углов из двух полуприемов – 6” для теодолита с окулярным микрометром и 8” – без; 2) расхождение углов из разных приемов 4 и 5” для сетей 1 и 2 классов соответственно; 3) колебание среднего значения угла, полученного по результатам непосредственных измерений и найденного из вычислений, не должно превышать 3 “ при n до 5 и 4” – более 5. Если законченные приемы не удовлетворяют этим допускам, то их переделывают на тех же установках круга. Если второй контроль не выполняется, то перенаблюдают углы, имеющие максимальное и минимальное значение, при тех же установках круга. Все наблюдения выполняют заново, если число повторных приемов более 30% от числа приемов, предусмотренных программой. Наблюдения повторяют и при несоблюдении третьего контроля.

С.к.о. единицы веса и уравненного угла определяют по формулам

.

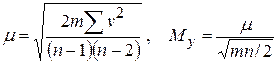
Достоинстваспособа: уравненные результаты являются рядом равноточных направлений; углы можно измерять в любой последовательности, выбирая наиболее благоприятные условия видимости и обеспечивая в итоге высокую точность; малая продолжительность одного приема (2-4 минуты измерения угла) обеспечивает меньшую зависимость точности результата от кручения сигнала; большое число перестановок горизонтального круга ослабляет влияние ошибок диаметров лимба.

Недостатки:быстрое уменьшение числа m приемов измеренного угла с ростом числа n направлений на пунктах (малое число приемов непосредственного измерения углов снижает точность их средних и уравненных значений); быстрый рост объема работ при n > 5.

Способ неполных приемовпредложен в 1954 г. Ю.А. Аладжаловым. Все направления разбивают на группы по три направления (без замыкания горизонта) так, чтобы определяемые по ним углы соответствовали бы углам, измеренным во всех комбинациях, но требовали бы меньшего объема работ и позволили увеличить число приемов непосредственных измерений каждой группы направлений. Следовательно, в этом способе заложено стремление избавиться от недостатков методов Струве и Шрейбера при наблюдении на пунктах с большим количеством направлений.

Практически не всегда путем подбора можно разбить направления на группы из трех направлений. В этом случае кроме групп из трех направлений измеряют отдельные углы, дополняющие программу. Программа измерений приведена в Инструкции. Способ неполных приемов применяется в триангуляции 2 класса на пунктах с 7 – 9 направлениями.

Обработка результатов измерений на станции заключается в определении средних значений направлений из m приемов в каждой группе и средних значений отдельных углов. По этим средним значениям вычисляют все углы – по три угла из каждой группы из трех направлений. Окончательно уравненные углы вычисляют по формулам способа Шрейбера. С.к.о. уравненных направлений определяют по формуле

,

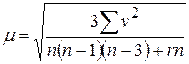
где v – разности между измеренными и уравненными значениями углов; n – число направлений на пункте; r – число отдельно измеренных углов в программе. Вес уравненных направлений

,

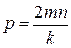
где m – число приемов измерений направлений и отдельных углов; n, k – число направлений на пункте и в группе соответственно (k = 3, для углов k = 2).

Достоинства способа: результаты уравнивания на станции равноточны; объем работы на пункте на 20 – 25% меньше, чем в способе Шрейбера; число приемов непосредственных измерений групп при n = 7 – 9 больше, чем в способе Шрейбера, что позволяет более полно ослаблять ошибки измерений; дает возможность измерять направления, на которые в данный момент имеется хорошая видимость; короткая продолжительность приема (2 – 4 минуты), что позволяет уменьшить зависимость точности измерений от качества сигнала.

Недостатки:отсутствуют правила образования групп из трех направлений; при n = 8 нужно измерять большое число отдельных углов, что приводит к неклторому нарушению равноточности уравненных направлений; программа не предусматривает ослабление односторонне действующих ошибок измерений.

Видоизмененный способ измерения углов в комбинацияхпредложен А.Ф.Томилиным. Используется в триангуляции 2 класса на пунктах с 6 – 9 направлениями. В этом способе на станции с n направлениями независимо измеряют 2n углов:

Каждый угол измеряют 5 или 6 приемами. В этом способе измеряют не все углы, образующие сочетания направлений из n по 2, поэтому результат уравнивания на станции не является рядом равноточных направлений, и формулы для вычислений поправок в измеренные углы являются довольно сложными.

Достоинстваспособа: при n =7 – 9 число приемов непосредственных измерений углов больше и их точность выше, чем в способе Шрейбера; требует меньшего объема измерений, чем способ во всех комбинациях.

Недостатки:сложные формулы для вычисления поправок в измеренные углы.

Источник