Способы измерения угла поворота

Метрология

Методы и средства контроля и измерения углов

Углы и измерение углов

Угловые размеры определяют положение плоскостей, осей, линий, центров отверстий и т. д. Угловые размеры бывают зависимые и назависимые.
Независимые углы не связаны с другими параметрами изделия; зависимые углы определяются основными параметрами изделий, к которым они относятся.

В качестве единицы измерения плоских углов Международной системой единиц (СИ) принят радиан — угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
Измерение углов в радианах на практике связано с значительными трудностями, так как ни один из современных угломерных приборов не имеет градуировки в радианах.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:

• 1 рад = 57°17׳45״ = 206 265″
• 1° = π/180 рад = 1,745329 × 10 -2 рад;
• 1‘ = π /10800 рад = 2,908882 × 10 -1 рад;
• 1” = π/648000 рад = 4,848137 × 10 -6 рад.

Значение угла при измерении определяют сравнением его с известным углом. Известный угол может быть задан так называемыми жесткими (с постоянным значением угла) мерами — аналогами формы элементов детали: угловыми мерами, угольниками, угловыми шаблонами, коническими калибрами, многогранными призмами.
Измеряемый угол можно сравнивать также с многозначными угломерными штриховыми мерами и различными видами круговых и секторных шкал. Еще одним методом получения известного угла является его расчет по значениям линейных размеров на основании тригонометрических зависимостей.

В соответствии с этим классификацию методов измерений углов производят в первую очередь по виду создания известного угла: сравнением с жесткой мерой, сравнением с штриховой мерой (гониометрические методы) и тригонометрическими методами (по значениям линейных размеров).

При сравнении углов с жесткой мерой отклонение измеряемого угла от угла меры определяют по просвету между соответствующими сторонами углов детали и меры, по отклонению показаний прибора линейных размеров, измеряющих несовпадение этих сторон или при контроле «по краске», т.е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.

В приборах для гониометрических измерений имеются штриховая угломерная шкала, указатель и устройство для определения положения сторон угла. Это устройство связано с указателем или шкалой, а измеряемая деталь — соответственно со шкалой или указателем. Определение положения сторон угла можно производить как контактным, так и бесконтактным (оптическим) способом. При соответствующих измеряемому углу положениях узлов прибора определяют угол относительного поворота шкалы и указателя.

При косвенных тригонометрических методах определяют линейные размеры сторон прямоугольного треугольника, соответствующего измеряемому углу, и по ним находят синус или тангенс этого угла (координатные измерения). В других случаях (измерение с помощью синусных или тангенсных линеек) воспроизводят прямоугольный треугольник с углом, номинально равным измеряемому, и устанавливая его как накрест лежащий с измеряемым углом, определяют линейные отклонения от параллельности стороны измеряемого угла основанию прямоугольного треугольника.

При всех методах измерений углов должно быть обеспечено измерение угла в плоскости, перпендикулярной к ребру двугранного угла. Перекосы приводят к погрешности измерения.

При наличии наклона плоскости измерения в двух направлениях погрешность измерения угла может быть и положительной и отрицательной. При измерениях малых углов эта погрешность не превысит 1% значения угла при углах наклона плоскости измерения до 8°. Такая же зависимость погрешности измерения угла от углов перекоса получается и в случаях неточного базирования деталей на синусной линейке, несовпадения направления ребра измеряемого угла или оси призмы с осью поворота на гониометрических приборах (при фиксации положения граней по автоколлиматору), при измерениях с помощью уровней и т.п.

Угол наклона плоскостей обычно определяется уклоном, численно равным тангенсу угла наклона.
Малые значения уклонов часто указывают в микрометрах на 100 мм длины, в промилле или миллиметрах на метр длины (мм/м).
Например, в мм/м указывается цена деления уровней. Пересчет уклонов в угол обычно производится по приближенной зависимости: уклон 0,01 мм/м (или 1 мкм/100 мм) соответствует углу наклона в 2″ (погрешность подсчета угла по этой зависимости составляет — 3%).

Как было показано выше в машиностроении в зависимости от используемых средств и методов различают три основных способа измерения углов :

Сравнительный метод измерения углов с помощью жестких угловых мер. При этом измерении определяется отклонение измеряемого угла от угла меры.

Абсолютный гониометрический метод измерения углов, при котором измеряемый угол определяется непосредственно по угломерной шкале прибора.

Косвенный тригонометрический метод: угол определяется расчетным путем по результатам измерения линейных размеров (катетов, гипотенузы), связанных с измеряемым углом тригонометрической функцией (синусом или тангенсом).

Сравнительный метод измерения углов обычно сочетается с косвенным тригонометрическим методом, последним определяется разница сравниваемых углов в линейных величинах на определенной длине стороны угла.

Угловые призматические меры и угольники

Угловые призматические меры служат для хранения и передачи единицы плоского угла. Их применяют для проверки шаблонов и угловых размеров различных изделий; для градиуровки угломерных приборов, а также для непосредственных измерений.
Угловые меры, предназначенные для проверки угломерных приборов и рабочих мер, называют образцовыми.

По точности аттестации образцовые угловые меры делят на четыре разряда (1,2,3 и 4). Предельные погрешности аттестации рабочих углов не должны превышать для угловых мер 1-го разряда — ±0,5”; 2-го разряда — ±1”; 3-го — ±3”; 4-го — ±6”.
Угловые меры собирают в блоки с помощью специальных державок.

Контроль углов угольниками осуществляют, оценивая просвет между угольником и контролируемой деталью на глаз, или сравнивают с образцовой щелью, созданной с помощью концевых мер длины и лекальной линейки.
При использовании крупных угольников просвет оценивают с помощью щупов.
Погрешность проверки углов угольником зависит от погрешности самого угольника, длины сторон угла, по которой производится проверка, и других факторов.

Угломеры с нониусами

Угломеры с нониусами применяют для измерения профиля угла на деталях контактным методом с отсчетом по угловому нониусу с точностью 2‘ и 5‘. Состоит угломер из круглого угломерного диска, скрепленного с корпусом зажимной гайкой. На основании смонтированы установочная планка и нониус с нанесенными 30 делениями с двух сторон от нулевого штриха; каждое деление соответствует 2 мин.
Линейка с лицевой стороны имеет продольный ласточкообразный паз, по которому перемешается (в процессе установки линейки на угол) хвостовик прижима.

При измерении угломер накладывают на проверяемую плоскость детали так, чтобы линейка и рабочая плоскость корпуса были совмещены со сторонами измеряемого угла. Целое число градусов отсчитывают по шкале диска до нулевого деления (штриха) нониуса. Затем определяют деление нониуса, совпадающего с делениями основной шкалы (диска).
После этого определяют по нониусу сколько минут и градусов совпадают с делениями нониуса.

Оптический угломер

В корпусе оптического угломера закреплен стеклянный диск со шкалой, имеющей деления в градусах и минутах. Цена малых делений 10 ‘. С корпусом жестко скреплена основная (неподвижная) линейка. На диске смонтированы лупа, рычаг и укреплена подвижная линейка.
Под лупой параллельно стеклянному диску расположена небольшая стеклянная пластинка, на которой нанесен указатель, ясно видимый через окуляр. Линейку можно перемещать в продольном направлении и с помощью рычага закреплять в нужном положении.

Во время поворота линейки в ту или другую сторону будет вращаться в том же направлении диск и лупа. Таким образом, определенному положению линейки будет соответствовать вполне определенное положение диска и лупы. После закрепления линеек зажимным кольцом через лупу отсчитывают показания угломера.
Оптическим угломером можно измерять углы от 0 до 180°. Допускаемые погрешности показания оптического угломера ±5‘.

Индикаторный угломер

В индикаторном угломере обычная шкала и нониус заменены индикаторным циферблатом. Отсчет угловых размеров производится по показаниям стрелки на большой шкале через 10°. Цена деления 5‘, предел измерения угломера 0…360°.

Портативный оптический угломер-шаблон

Портативный оптический угломер-шаблон предназначен для проверки профиля резцов. Он состоит из стандартной восьмикратной лупы, неподвижно закрепленной на прозрачном диске из органического стекла. Вокруг оси, запрессованной в этот диск, свободно поворачивается стальной диск, по периметру которого с высокой точностью выполнены шаблоны наиболее часто встречающихся в практике углов, радиусов и кривых. Нужный профиль шаблона накладывают на затачиваемый резец и под лупой проверяют точность доводки.
Прибор отличается точностью и удобством, так как им можно пользоваться непосредственно на рабочем месте.

Источник

Угол поворота, угол произвольной величины

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

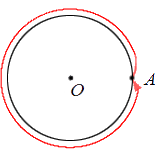
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Полный оборот

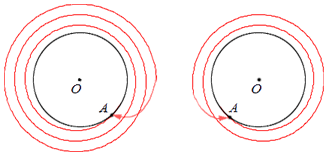
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Направление поворота

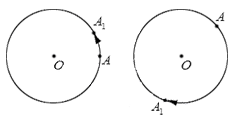
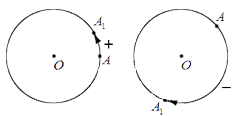
Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

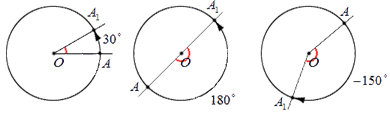
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

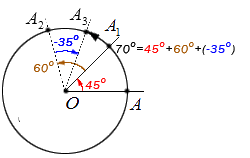
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Источник