Способы измерения расстояния до луны

Как рассчитать расстояние до Луны без телескопа и СМС-регистрации

В комментариях к моему прошлому посту отметили, что я не расписал, как древнегреческие астрономы высчитали расстояние до Луны. Вот этой теме и посвящен следующий текст. Правда, задача оказалась проще, чем с расстоянием до Солнца, поэтому и пост получится заметно покороче.

Начну с того, что у античной науки была одна особенность: и греки (и затем римляне) фактически не умели в алгебру, они не пользовались десятичными дробями, понятием ноля, даже система счисления у тех и других была алфавитная, а не позиционная. Но зато они хорошо научились решать геометрические задачи. И познавали мир с помощью геометрии.

В частности, рассчитали расстояние до Луны. Как раз Аристарх Самосский считается первым, кому это удалось. И сделал он это следующим образом (излагаю кратко, кому нужно больше подробностей – читайте в первоисточнике, кому нужно много формул — это тоже есть в Сети, например, здесь).

Сначала он измерил угловой радиус нашего спутника. Зная его, можно рассчитать «сколько» Лун можно разместить на ее орбите. Это количество, согласно формуле длины окружности, равняется произведению радиуса орбиты (того самого расстояния) на 2 π. Теперь, для того, чтобы высчитать радиус, Аристарху нужно было рассчитать не угловой, а фактический размер Луны.

Кратко его дальнейшее решение звучало так. Затмения доказывали, что Солнце находится дальше от Земли, чем Луна, а их угловые размеры примерно равные (по расчетам Аристарха). На основании этого астроном сделал вывод, что солнечные лучи, падающие на Луну, сходятся за ней в точку на поверхности Земли. Далее он измерил тень от Земли на диске Луны во время лунного затмения. Тень получилась в два раза больше, чем сама Луна.

Аристарх суммировал результаты обоих выводов (разница в тенях и «уход» солнечных лучей от диаметра в точку) и пришел к выводу, что Луна меньше Земли в три раза. Это было довольно близко к современному ответу – в 3,6 раза.

Итак, Аристарх посчитал, что Луна «укладывается» на орбиту 720 раз и она меньше Земли в 3 раза. Значит Земля «поместилась» бы на лунной орбите 240 раз. Диаметр Земли грекам был известен благодаря Эратосфену (и это было очень близкое к реальному значение). Теперь формула расчета радиуса лунной орбиты была довольно простой: 240 диаметров Земли разделить на 2 π. У Аристарха получилось 486400 км.

Спустя сто лет другой античный астроном Гиппарх уточнил его расчеты: в его ответе Луна помещалась на орбиту всего 650 раз, а расстояние получалось уже около 382 тыс. километров. Что всего на пару тысяч километров расходится с современными данными.

Источник

Способы измерения расстояния от Земли до Луны в километрах и метрах и сколько лететь по времени

Измерение расстояния от Земли до Луны проводились еще в древние времена: греки пытались сделать это неоднократно.

Данные сведения были необходимы человеку для получения полноценной картины представления о Вселенной.

Кроме вычислений о расстоянии до спутника Земли, древние греки проводили расчеты, чтобы вычислить его радиус.

Со временем технологический прогресс развивался и уже сегодня все измерения известны человеку.

Как вычислялось расстояние?

Издавна людям было интересно, что же представляется собой космос и Луна – она с незапамятных времен была естественным спутником нашей планеты.

Люди интересовались, как далеко она находится и сколько до нее лететь, применяя для этого разнообразные подсчеты.

На сегодняшний день измерить расстояние методами, использующимися в повседневной жизни – нереально.

Для этого применяются тригонометрические формулы и расчеты.

Рассмотрим, как древние люди определяли этот показатель, напоминая, что он измеряется от центра спутника:

Первый, кто попытался достучаться до истины, был Аристарх Самосский.

На основе геометрических уравнений и показателей, полученных с помощью угломерных инструментов, ученый проводил исследование.

Для начала он вычислил разницу расстояния до спутника и Солнца, после чего умножал данный результат на радиус Земли. Его расчеты показали, что расстояние равно 509680 в километрах.
Во 2 веке до нашей эры астроном Гиппарх Никейский также принялся за вычисления.

Он проводил наблюдения за Луной при разных ее фазах и пришел к выводу, что расстояние до Земли будет равно 382260 километров.

Основываясь на угловых замерах, Гиппарх выяснил, что в период затмения Солнце и Луна имеют одинаковые показатели.

После этого он высчитал разницу и вывел формулу, по которой определил среднее расстояние.

Среднее расстояние в километрах

Указать точные показатели расстояния в километрах невозможно: это связано с эллиптической формой орбиты, по которой движется спутник.

Это говорит о том, что некоторое время он удаляется от планеты, после чего снова приближается.

Реальные размеры могут изменяться в пределах 15 %, что связано с различными точками нахождения спутника.

Самая полная Луна находится к Земле гораздо ближе, чем тогда, когда она проходит фазу роста.

Известные показатели помогут узнать расстояние, которое измерили ученые:

Показатель	Описание
384403 километров	Астрономы называют данное расстояние большой полуосью, оно измеряется только километрами, величина в метрах здесь не используются. Иногда приводятся цифры 384467 километров, что не является верным
357104 километра	Такой результат является минимальным числовым показателем, когда Луна находится в самой близкой точке к Земле
406696 километров	В апогее спутник располагается на указанном количестве километров от Земли – его самая отдаленная точка будет показывать данное число

Время полета

На сегодня уже совершено большое количество полетов, для того, чтобы судить, сколько по времени занимает путешествие до спутника.

Ученые производили расчеты, исходя из скорости на ракете и наблюдения за космонавтами.

Вот некоторые цифры:

Самый медленный полет займет 1 год 1 месяц и 2 недели, что было доказано при эксперименте.

В 2003 году на основе станции с ионным революционным двигателем под названием ЕКА SMART-1 был произведен запуск лунного зонда.

Средний по времени полет занял 5 дней, когда китайский спутник Chang’e-1 был отправлен в 2007 году на орбиту: при полете использовались стандартные ракетные двигатели.

Пилотируемый полет с человеком длился 3 дня 3 часа и 49 минут, когда американцы в 1969 году впервые ступили на поверхность Луны – космический корабль Сатурн-5 стартовал с площадки во Флориде.

Кратчайший путь освоили американцы в проекте «Новые горизонты»: скорость спутника составляет 58 тысяч километров.

Чтобы преодолеть притяжение Солнца, компания Nasa использовала огромное ускорение.

Сегодня туристические космические компании по всему миру предлагают путешествия на Луну короткой или длительной продолжительности.

Интересные факты

Любые вычисления, произведенные человеком, были окружены множеством интересных фактов, историй. Измерение пространства и расстояния до Луны не лишено таких случаев.

Приведем несколько интересных примеров, связанных с историей вычисления времени полета, расстояния от Земли до спутника:

1. Согласно легенде, Луна образовалась от столкновения планеты Земля с другой планетой. Тогда образовалась орбита, из которой сформировался спутник желто-белого цвета.
2. Спутник всегда обращен к планете одной стороной.
3. Самый большой кратер называется Бэйли, его диаметр составляет 295 километров.
4. Во время одной из экспедиций американский Аполлон-6 привез на Землю несколько сотен килограммов лунного грунта.
5. Находясь на Земле и смотря в небо, кажется, что Луна и Солнце обладают одинаковыми размерами.
6. На Луне нет атмосферы, поэтому ночь там наступает сразу, без постепенного угасания света.
7. Сила притяжения на спутнике имеет наименьшее значение – она в 6 раз меньше силы притяжения на Земле.
8. На поверхности спутника существует памятник погибшим космонавтам – это фигура 10 сантиметров из алюминия.
9. С течением лет Луна значительно отдалилась от Земли: это происходит каждый год на 4 сантиметра.
10. Минимальное расстояние в ближайших точках от Луны до Марса составляет 55 миллионов 399 тысяч километров.

Известно, что в будущем планируются регулярные полеты на Марс, однако гораздо удобнее осуществлять их с поверхности спутника.

Вычисление расстояний до Луны помогает организаторам полетов достоверно просчитать количество топлива, а также средств, затрачиваемых на полет.

Полезное видео

Источник

Как измерили расстояние от Земли до Луны?

Расстояние от Земли до Луны пытались измерить еще древние греки.

До нас дошло только сочинение Аристарха Самосского «О величинах и расстояниях Солнца и Луны» (III в. до н. э.), где он впервые в истории науки попытался установить расстояния до этих небесных тел и их размеры.

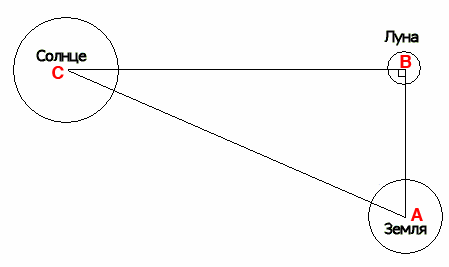
К решению этого вопроса Аристарх подошел очень остроумно. Он исходил из предположения, что Луна имеет форму шара и светит отраженным от Солнца светом. В этом случае, в те моменты, когда Луна имеет вид полудиска, она образует прямоугольный треугольник с Землей и Солнцем:

Если в этот момент точно определить угол между направлениями с Земли на Луну и на Солнце (CAB), можно из простых геометрических соотношений найти, во сколько раз катет (расстояние от Земли до Луны AB) меньше гипотенузы (расстояния от Земли до Солнца AC). По Аристарху, CAB=87°; следовательно, соотношение этих сторон 1:19.

Аристарх ошибся приблизительно в 20 раз: в действительности расстояние до Луны меньше, чем до Солнца, почти в 400 раз. Загвоздка заключается в том, что точно определить момент, когда Луна оказывается в вершине прямого угла, лишь на основе наблюдений невозможно. Малейшая же неточность влечет за собой огромное отклонение от истинного значения.

Величайший астроном древности Гиппарх Никейский в середине II века до н. э. с большой уверенностью определил расстояние до Луны и ее размеры, приняв за единицу радиус земного шара.

В своих вычислениях Гиппарх исходил из правильного понимания причины лунных затмений: Луна попадает в земную тень, имеющую форму конуса с вершиной, находящейся где-то в стороне Луны.

Посмотрите на рисунок. Он показывает положение Солнца, Земли и Луны во время лунного затмения. Из подобия треугольников следует, что расстояние от Земли до Солнца AB во столько раз больше расстояния от Земли до Луны BC, во сколько раз разность радиусов Солнца и Земли (AE — BF) больше разности радиусов Земли и ее тени на расстоянии Луны (BF — CG).

Из наблюдений при помощи простейших угломерных инструментов следовало, что радиус Луны составляет 15′, а радиус тени приблизительно 40′, то есть радиус тени больше радиуса Луны почти в 2,7 раза. Приняв расстояние от Земли до Солнца за единицу, можно было установить, что радиус Луны почти в 3,5 раза меньше радиуса Земли.

Уже было известно, что под углом в 1′ наблюдается предмет, расстояние до которого превосходит его размеры в 3 483 раза. Следовательно, рассуждал Гиппарх, под углом в 15′ наблюдаемый предмет будет в 15 раз ближе. Значит, Луна находится от нас на расстоянии, в 230 раз (3 483 : 15) превосходящем ее радиус. А если радиус Земли составляет приблизительно 3,5 радиуса Луны, то расстояние до Луны равно 230 : 3,5

60 радиусов Земли, или около 30 земных диаметров (это около 382 тыс. километров).

В наше время измерение расстояния от земли до Луны было выполнено с помощью метода лазерной локации. Суть этого метода заключается в следующем. На поверхности Луны устанавливается уголковый отражатель. С Земли с помощью лазера на зеркало отражателя направляется лазерный луч. При этом точно фиксируется время, когда сигнал был излучён. Отражённый от прибора на Луне свет в течение примерно одной секунды возвращается в телескоп. Определив точное время, за которое луч света проходит расстояние от Земли до Луны и обратно, можно установить расстояние от источника излучения до отражателя.

С помощью этого метода расстояние от земли до Луны определено с точностью до нескольких километров (максимальная точность измерения в настоящее время — 2-3 сантиметра!): в среднем оно составляет 384 403 км. «В среднем» не потому, что это расстояние взято из разных или приблизительных результатов измерений, а потому, что орбита Луны представляет собой не окружность, а эллипс. В апогее (наиболее удаленная от Земли точка орбиты) расстояние от центра Земли до Луны 406 670 км, в перигее (наиболее близкая точка орбиты) — 356 400 км.

Источник

Как далеко до Луны?

Как без помощи Google, Википедии и NASA узнать расстояние от Земли до Луны

Представьте, что вы смотрите на луну зимним вечером и задаетесь вопросом: «Как далеко находится Луна?». Что бы вы сделали, чтобы рассчитать, насколько это далеко? Самое простое решение — заглянуть в Google. Но, как же тогда греки, которые задавали тот же вопрос 2200 лет назад, и нашли ответ на него без помощи Google, Википедии и NASA или любой современной технологии? Греки смогли определить достаточно точное расстояние от Земли до Луны, используя тщательные наблюдения, измерения и изящную геометрическую модель.

Определение ключевой информации

Греческий астроном и математик, Аристарх Самосский, вычислил расстояние от Земли до Луны только пользуясь следующей информацией:

• Диаметр Земли равняется приблизительно 8 000 миль или 12 800 км (еще один гениальный расчет, сделанный Эратосфеном).

• Тени, отбрасываемые небесными телами, имеют коническую форму и считаются похожими. В двумерном виде тени, отбрасываемые Луной и Землей, являются подобными равнобедренными треугольниками:

Следующая информация была получена в результате пристального наблюдения лунных затмений.

• Во время полного лунного затмения наблюдалось, что Луна проходила через земную тень расстояние, равное диаметру двух с половиной своих дисков.

Формулирование модели

На основе этой информации была разработана модель. В этой модели тень от Луны разворачивается зеркально по отношению к земной тени, а сама Луна располагается так, что одна сторона её тени выравнивается с одной стороной земной тени. При этом конец лунной тени сужается достигая Земли.

Пусть диаметр Луны равен 1 единице. Тогда AF составляет 1 единицу, а FD должен составлять 2,5 единицы, что согласуется с наблюдениями за лунными затмениями.

Как указывалось выше, треугольники теней — ABF и BEC подобны. Следовательно углы BEC и ABF равны. Из этого следует, что линии AB и EC взаимно параллельны. Также параллельны линии AD и BC. Поэтому прямоугольник ABCD является прямоугольником, в котором противоположные стороны равны. А, следовательно, BC = AD.

ВС — это диаметр Земли, который, как известно из исходных данных, составляет примерно 8 000 миль или 12 800 км.

AD — это 3,5 диаметра Луны. Из равенства ВС=AD можно рассчитать этот диаметр, который будет равен примерно 2 285 миль (8000/3,5) или около 3 500 км.

Основываясь на информации, с которой мы начали, расстояние между Землей и Луной составляет 108 диаметров Луны или примерно 378 000 км (3500 x 108).

Современные расчеты показывают, что расстояние от Земли до Луны из-за эллиптической орбиты спутника колеблется от 363 тыс.км (перигей) до 406 тыс.км (апогей), а большая полуось орбиты составляет 384 тыс.км. Невероятно, но Аристарху удалось сделать достаточно точную оценку этого расстояния, учитывая инструменты, которые он имел в своем распоряжении, и астрономические масштабы, с которыми он работал.

Источник