Методы измерений и погрешности измерений
Метод измерений — прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений.
По общим приемам получения результатов измерений различают: 1) прямой метод измерений; 2) косвенный метод измерений. Первый реализуется при прямом измерении, второй — при косвенном измерении.
В соответствии с РМГ 29-99, к числу основных методов измерений относят метод непосредственной оценки и методы сравнения: дифференциальный, нулевой, замещения и совпадений.
Непосредственный метод — метод измерений, в котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия, например измерения силы тока амперметром.
Методы сравнения с мерой — методы, при которых измеряемая величина сравнивается с величиной, воспроизводимой мерой:
- дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Примером дифференциального метода может служить измерение вольтметром разности двух напряжений, из которых одно известно с большой точностью, а другое представляет собой искомую величину;
- нулевой метод — при котором разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины, например измерительный мост;
- метод замещения — метод сравнения с мерой, в котором измеренную величину замещают известной величиной, воспроизводимой мерой. Метод замещения применяется при измерении сопротивления с поочередным замещением его из магазина сопротивлений;
- метод совпадений — метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. Примером использования данного метода может служить измерение частоты наблюдением при помощи осциллографа фигур Лиссажу.
Погрешности измерений. Процесс измерения неизбежно сопровождается ошибками, которые вызываются несовершенством измерительных средств, нестабильностью условий проведения измерений, несовершенством самого метода и методики измерений, недостаточным опытом и несовершенством органов чувств человека, выполняющего измерения, а также другими факторами.
Погрешность измерения, выраженная в единицах измеряемой величины, называется абсолютной. Она не всегда является информативной. Например, абсолютная погрешность 0,01 мм может быть достаточно большой при измерениях величин в десятые доли миллиметра и малой при измерениях величин, размеры которых превышают несколько метров.
Более информативной величиной является относительная погрешность, под которой понимают отношение абсолютной погрешности измерения к ее истинному значению (или математическому ожиданию).
Именно относительная погрешность используется для характеристики точности измерения.
По своему характеру (закономерностям проявления) погрешности измерения подразделяются на систематические, случайные и грубые промахи.
К систематическим погрешностям измерений относят погрешности, которые при повторных измерениях остаются постоянными или изменяются по какому-либо закону.
Систематические погрешности измерения при измерении одним и тем же методом и одними и теми же измерительными средствами всегда имеют постоянные значения. К причинам, вызывающим их появление, относят:
- погрешности метода или теоретические погрешности;
- инструментальные погрешности;
- погрешности, вызванные воздействием окружающей среды и условий измерения.
Случайные погрешности измерений – это погрешности, принимающие при повторных измерениях различные, независимые по знаку и величине значения, не подчиняющиеся какой-либо закономерности.
Влияние случайных погрешностей измерений выражается в разбросе полученных результатов относительно математического ожидания, поэтому количественно наличие случайных погрешностей хорошо оценивается среднеквадратическим отклонением (СКО).
Случайные погрешности измерений, не изменяя точности результата измерений, тем не менее, оказывают влияние на его достоверность.
При этом дисперсия среднего арифметического ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то количество измерений надо увеличить в 4 раза.
Грубые погрешности измерений (промахи) — это погрешности, приводящие к явным искажениям результатов измерения.
При оценке грубых промахов прибегают к обычным методам проверки статистических гипотез.
Источник
Способы измерения погрешностей при измерениях
1. Методы измерений.
2. Погрешности измерений.
3. Выбор метода и средств измерений.
4. Выбор измерений.
1. Методы измерений . Измерение физической величины может быть осуществлено различными методами (способами), выбор которых в каждом отдельном случае зависит от характера измеряемой величины, от условий измерения, от устройства и принципа действий измеряемой аппаратуры, а также требуемой точности.
По способу получения числового значения измеряемой величины методы измерения делят на 3 вида:
Они различаются по характеру использования мер.
К наиболее важным методам, прямых измерений постоянно встречающихся на практике, относятся следующие:
1. Метод непосредственной оценки.
2. Метод сравнения, состоящий из четырех разновидностей:
а) нулевой метод;
б) дифференциальный метод;
в) метод замещения;
г) метод совпадения.
Сущность метода непосредственной оценки Состоит в том, о значение измеряемой величины судят по показанию одного или нескольких приборов прямого преобразования, заранее проградуированных в единицах измеряемой величины или в единицах других величин, от которых зависит измеряемое. Он принадлежит к числу наиболее распространенных в технической практике (в силу своей простоты), и типичным его примером служит измерение электрических величин стрелочными приборами. Точность этого метода обычно ограничивается точностью измерительных приборов. Отличительной особенностью этого метода является то, что мера непосредственного участия в процессе измерения не принимает.
Сущностью метода сравнения является то, что при использовании этих методов измеряемая величина в процессе измерения сравнивается с величиной, воспроизводимой мерой.
Таким образом, отличительной чертой методов сравнения является непосредственное участие меры в процессе измерения. Они различаются по характеру использования мер.
А) Нулевой метод – это метод, при котором результатирующий эффект воздействия измеряемой величины и образцовой меры на прибор сравнения (нулевой индикатор) доводится до нуля. Примерами использования нулевых методов в электротехнике являются мостовые и компенсационные схемы. Нулевые методы значительно сложнее методов непосредственной оценки, требуют значительно большего времени, но зато точность их несравненно выше (0,02% и выше).
Нулевые методы применяются в основном при проверке приборов используемых непосредственной оценке.
Б) Дифференциальный метод – это метод, при котором непосредственно оценивается измерительными приборами разность между измеряемой величиной и образцово мерой или разность производимых ими эффектов.
Аиз-А=а
Аиз – измеряемая величина; А – показание прибора; а – погрешность.
Зная А и измерив а, можно найти Аиз. Точность этого метода тем выше, чем меньше измеряемая разность и с тем большей точностью она измерена (если разность между Аиз и А составляет 1% и измерено с точностью до 1%, то точность измерения составит уже 0,01%).
Дифференциальные методы используются при точных лабораторных измерениях (поверка образцовых сопротивлений, поверка измерительных трансформаторов и др.).
В) Метод замещения . Этот метод заключается в том, что в процессе измерения измеряемая величина Аиз заменяется в измерительной установки известной величиной А, при чем путем измерения величины А, измерительная установка приводится в прежнее состояние, то есть достигаются те же показания приборов, что и при действии величины Аиз. При таких условиях Аиз=.
Г) Метод совпадения . Этот метод заключается в том, что измеряют разность между искомой величиной и образцовой мерой, используя совпадения меток шкал или периодических сигналов. Сущность этого метода можно пояснить на примере определения размера дюйма.
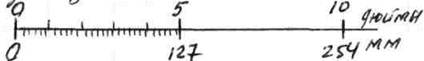 |
Погрешности измерений.
При осуществлении измерений, вследствие ряда причин, числовое значение измеряемой величины, полученная в результате опыта, является лишь более менее приближенным.
Отклонение результатов измерения от истинного значения измеряемой величины называется Погрешностью измерения .
Верным (истинным) значением Изменяемой величины называют ее значение, свободное от погрешностей измерений.
Действительное значение – это значение, полученное в результате измерения с допустимой погрешностью (ошибкой).
Погрешности измерений можно классифицировать по ряду признаков:
1. По способу числового выражения погрешности измерений делятся на:
А) Абсолютные и б) относительные.
Абсолютной погрешностью Называется разность между измеренным и действительным значением измеряемой величины.
За действительные значения измеряемой величины принимаются показания образцового прибора.
Абсолютная погрешность измеряется в единицах измеряемой величины.
Величина обратная по знаку абсолютной погрешности называется поправкой.
σ =-ΔА
Относительной погрешностью Называется отношение абсолютной погрешности к действительному значению измеряемой величины.
β = ΔА/АД = Аиз – Ад/Ад; или β = ΔА/Ад·100%.
2. По характеру изменения Погрешности измерений делятся на:
В) грубые ошибки (промахи).
Систематическими Называются погрешности, подчиняющие определенному закону или остающиеся в
Процессе измерения постоянными. К ним относятся погрешности, обусловленные неточностью осуществления меры, неправильностью градуировок измерительного прибора, влиянием температуры окружающей среды на меры и измерительные приборы.
Различают следующие разновидности систематических погрешностей:
2. Погрешности установки прибора.
3. Личные погрешности (субъективные).
4. Погрешности метода (или теоретические).
В зависимости от изменения во времени систематические погрешности делятся на: а) постоянные; б) прогрессивные; в) периодические.
Для учета и исключения систематических погрешностей необходимо располагать, возможно, полными данными о наличии отдельных видов погрешностей и о причинах их возникновения.
Систематические погрешности могут быть исключены или значительно уменьшены устранением источников погрешностей или введением поправок, останавливаемых на основании предварительного изучения погрешностей, путем поверки мер и приборов, используемых при измерении, введением поправочных формул и кривых, выражающих зависимость показаний приборов от внешних условий.
Случайными Называются погрешности, изменение которых не подчиняется какой-либо закономерности. Они обнаруживаются при многократном измерении искомой величины, когда повторные измерения проводятся одинаково тщательно и, казалось бы, при одних и тех же условиях.
Случайные погрешности нельзя исключить опытным путем, но их влияние на результат измерения может быть теоретически учтено путем применения при обработке результатов измерений методов теории вероятности и математической статистики.
Грубые ошибки – это погрешности, существенно превышающие ожидаемые при данных условиях. Примером грубых ошибок могут быть неправильные отсчеты показаний средств измерений. Грубые погрешности измерения выявляются при повторных измерения и должны быть отброшены, как на заслуживающие доверия.
Общие методы повышентя точностсти средств измерений.
Стремясь к созданию более точных средств измерений измерительная тезника выработала ряд общих методов достижения точности, которые можно подразделить на четыре группы:
1. Стабилизация важнейших параметров средств измерений технологическим путем, т. е. путем использования наиболее стабильных деталей, материалов и соответствующей технологии изготовления.
2. Метод пассивной защиты от быстро изменяющихся влияющих величин, т. е. уменьшение случайных погрешностей средств измерений путем применения фильтрации, амортизации, теплоизоляции и т. д.
3. Методы активной защиты от медленно изменяющихся влиящих величин путем стабилизации этих величин.
4. Методы коррекции систематических и прогрессирующих погрешностей и статическая обработка случайных погрешностей.
Повышение точности измерений обычно связано с усложнением аппаратуры и увеличением времени
(большая повторность) измерения. А это не всегда оравдано. Очевидно также нецелесообразность особой точности измерения величин, мало влияющих на числовое значение общего конечного результата.
Так, например, при измерении величин x1, x2 и х3 для определения величины у=х12*х2β*х3γ вряд ли целесообразно добиваться особой точности измерения х1, если показателем степени α =1, β = 2, γ = 3.
Требуемеая точность должна соответствовать задачам и условиям измерений.
Выбор метода и средств измерений.
При выборе метода измерений следует руководствоваться требуемой точностью результатов измерений.
По точности получаемых результатов можно разделить на три группы:
1. Результат измерения должен иметь максимальную возможную при существующем уровне измерительной техники точность.
Такие измерения называют Точными (презиционными). Например, измерения физических констант, эталонный измерения, некоторые спеиальные измерения, относящиеся к максимально точной работе отдельных приборов.
2. Измерения, погрешности результата которых не должена превосходить некоторого заданного значения.
Такие измерения называют Контрольно поверхностными. Они выполняются в поверочных контрольно-измерительных лабораториях такими измерительными средствами и по такой методике, чтобы гарантировать погрешность результата, не превышающую некоторого заранее заданного значения.
3. Измерения, при которых погрешность результата определена характеристиками измерительных устройств.
Такие измерения называют Техническими.
К ним относятся и лабораторные измерения, проводимые при различного рода обработок и исследованиях, и исследованиях, и производственные, и приемно-сдаточные, и эксплутационные измерения, проводимые для обеспечения необходимого режима работы различных объектов и устройств.
Приборы для измерений выбирают по ряду показателей: роду тока, частоты, диапозону измеряемой величины, точности, входным параметрам, степени влияния внешних факторов.
1. Род тока исследуемой цепи определяет принцип действия и систему выбираемого для нее измерительного прибора. (U, I, R на постоянном токе – МЭ, Р-ЭД, точное измерение I, U, P, cosγ вольтметру – ср. Д., измерения средних, действующих значений тока и напряжения в цепях передоваемого тока звуковой и высокой частоты применяют – выпрямительные, тэрмоэлектрические, электронные и электростатические приборы. Мгновнные значения переменных величин измеряют – осцелографами).
2. Номинальная чатота или область частоты измерительного прибора или меры должна соответствовать частоте тока исследуемой цепи.
Чем сильнее отличается частота исследуемой цепи от номинальной частоты прибора или меры, тем больше погрешности измерений.
3. Номинальные пределы прибора или меры не должны превышать верхнего предела измеряемой величины более чем на 25%.
Чем сильнее они разняться, тем менее точны результаты измерений. При заданном классе точности допускается относительная погрешность прибора или меры тем больше, чем меньше измеряемая величина.
4. Классы точности выбранного измерительного прибора или меры должны быть такими, чтобы допустимые основные погрешности были в 3 раза меньшими, чем допустимые погрешности данных измерений, т. к. предельная погрешность измерений, возможная в данных условиях, не может превысить
Утроенного значения среднеквадратичной погрешности ряда измерений.
5. В зависимости от схемы включения измерительного прибора его входное сопротивление должно быть, возможно, большим или меньшим.
Чем точнее измерения, тем большими должны быть входные сопротивления измерительных приборов включаемых параллельно, и тем меньшими они должны быть у приборов, включаемых последовательно в исследуемую цепь.
6. Выбирая нужный измерительный прибор, следует учитывать конкретные условия измерений и технические характеристики прибора.
Непосредственное влияние внешних факторов может вызвать большие погрешности приборов (температура, влажность, внешние электрические и магнитные поля, паразитные емкости). При любых условиях наиболее желательны приборы и меры, требующие минимальных средств защиты от влияния внешних факторов.
Виды измерений.
Прцесс измерения может осуществляться по-разному в зависимости от рода измеряемой величины и приемов измерения.
По способу получения результатов различабт следующие виды измеренй:
2. Косвенные измерения.
3. Совокупные измерения.
К прямым измерениям Относятся измерения, результат которых получается непосредственно из опытных данных измерения.
Прямое измерение условно можно выразить формулой Y=Х, где
Y – искомое значение измеряемой величины;
Х – значение, непосредственно получаемоеиз опытных данных.
К этому виду измерений относятся измерения различных физичских величин при помощи приборов, градуированных в установленных единицах (ток – апмерметром, температура – термометром). К этому виду измерений относятся и измерения, при которых искомое значение величины определяется непосредственным сравнением ее с мерой.
Косвенными Называется такое измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвеных измерениях числовое значение измеряемой величины определяют путем вычисления по формуле.
Y = F (X1, X2, … , Xn),
где y – искомое значение измеряемой величины;
x1, x2, …, xn – значения измеренных величин (R = U/I, P = U*I – в цепях постоянного тока).
Совокупными Называются такие измерения, при коорых искомые значения величин определяются путем решения системы уравнений, связывающих значения искомых величин с непосредственно измеренными величинами, т. е. путем решения системы уравнений.
Примером этого вида измерений является определение температурных коэффициентов сопротивления:
Rt = R20 [1+α (T1-20)+β(T1-20)]
Здесь Rt и t измеряются прямым измерением, а α, β и R20 – искомые величины.
Меняя тепловой режим катушки и измеряя Rt при ряде заданных температур t1; t2 и t3, получаем систему уравнений, совместное решение которых позволяет определить числовые значения искомых величин.
Источник




