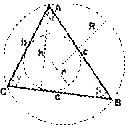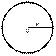Способы измерения площадей геометрических фигур

Площадь фигуры, её свойства. Способы измерения площадей фигур. Единицы площади. Вычисление площадей квадрата, прямоугольника, треугольника, круга, трапеции.

Первое представление о площадях – в дошк. возрасте (н-р: сравнивая платочки).Геометр фигура плоская, если все точки принадлежат 1 плоскости. S фигуры – положит величина, определяется для каждой фигуры, так что: 1) равные фигуры имеют = S; 2) S фигуры = сумме S всех ее компонентов. Равные фигуры – совпадают при наложении. Равновеликие – S равны. Равносоставленные – две фигуры, которые можно разбить на соответ равные части (только многоугольники). Теорема Бойян и Гервина: 1) равносоставленные фигуры = равновеликие; 2) если у 2 многоугольников S =, то их можно представить из 2 попрано = частей.

Св-ва S: 1)если фигуры =, то = их числ значения S; 2) если фигура состоит из частей, то S = сумме S этих частей; 3) при замене ед S, числ значение S увеличивается во столько раз, во сколько ед S; 4) числ значение S единичного квадрата = 1; 5) если F₁ – часть F₂, то численное значение F₁ 2 2 . Чтобы найти приближенное значение S_(F) достаточно сложить получ числовые значения S по недостатку и по избытку :2. S_(F)

(me+(m+n)e 2 )/2 = ((m+n+m)e 2 )/2= (2m/2 +n/2)e 2 = (m+n/2)e 2 . Для более точно значения – более мелкая палетка, или наклонить с разных углов, и высчитать среднее арифметическое.

Ед S. м 2 , см 2 , дм 2 , км 2 , мм 2 , ар, га, сотка.

Формулы площади квадрата

1) Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны. S = a2

2) Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b, где S — Площадь прямоугольника, a, b — длины сторон прямоугольника.

Формулы площади треугольника

1) Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. S = 1 a · h

2) Формула площади треугольника по трем сторонам

Формула Герона: S = √p(p — a)(p — b)(p — c)

3) Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S = 1 a · b · sin γ

4) Формула площади треугольника по трем сторонам и радиусу описанной окружности.

5) Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r, где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

Формулы площади круга

1) Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи. S = π r2

2) Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи. S = 1 π d2

где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

Формулы площади трапеции

1) Формула Герона для трапеции

S = a + b √(p — a)(p — b)(p — a — c)(p — a — d)

2) Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

где S — площадь трапеции,a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p = a + b + c + d — полупериметр трапеции.

Источник

Площадь фигуры. Способы измерения площадей фигур. Равновеликие и равносоставленные фигуры. Нахождение площади прямоугольника

Каждый представляет, что такое площадь комнаты, площадь участка земли. Так же понимает если земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат.

Это обыденное представление о площади. Но когда говорят о площади геометрической фигуры выделяют определённый класс фигур. Например, рассматривают площадь многоугольника, площадь поверхность многоугольника и другое.

Площадью фигуры называется положительная величина определенная для каждой фигуры так, что:

1. Равные фигуры имеют равные площади;

2. Если фигура состоит из двух частей, то ее площадь ровна сумме площадей этих частей.

Чтобы измерить точно площадь фигуры, нужно иметь единицу площади. Такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой Е, а число, которое получается в результате измерения площади – S(F). Это число называют численным значением площади фигуры F при выбранной единице площади E. Оно должно удовлетворять условиям:

1. Число S(F) – положительное.

2. Если фигуры равны, то равны численные значения их площадей.

3. Если F состоит из F1 и F2, то численное значение площади фигуры равно сумме численных значений площадей F1 и F2.

4. При замене единице площади численное значение площади данной фигуры увеличивается (уменьшается) во столько же раз, во сколько новая единица меньше (больше) старой.

5. Численное значение площади единичного квадрата принимается равным 1, т.е. S(F)=1.

6. Если фигура F1 является частью фигуры F2, то численное значение площади фигуры F1 не больше численного значения площади фигуры F2.

Фигуры, у которых площади равны, называются равновеликими.

Многоугольники F1 и F2 называются равносоставленными, если их можно разбить на соответственно равные части.

Любые два равновеликих многоугольника равносоставлены.

Теорема.Площадь прямоугольника равна произведению длин соседних его сторон.

Читайте также: А касательное напряжение (сила, действующая на единицу площади) Агентские сети и способы стимулирования их активности Активные способы проверки домашнего задания Альтернативные способы получения и преобразования энергии. Альтернативные способы получения электрической энергии. Амортизация основных средств, способы начисления амортизационных сумм. Аналоговые каналы передачи данных; способы модуляции, модемы Б7.5 Способы оказания первой помощи пострадавшему при поражения электрическим током. Б8.5 Способы проведения искусственного дыхания и наружного массажа сердца. Бак прямоугольной формы с водой имеет в дне малое отверстие, через которое происходит его опорожнение. Время опорожнения бака _____ раза, если площадь бака увеличить в 4 раза.

E

F Дано:

F – данный прямоугольник

a,b – длины его сторон.

Доказать: S(F) = ab

1. Пусть a и b – натуральные числа. Тогда прямоугольник F можно разбить на единичные квадраты: F = E+E+E…+E. Всего их ab, так как имеем b рядов, в каждом из которых a квадратов. Отсюда S(F)=S(E)+S(E)…+S(E) = abS(E) =ab

Для приближенного измерения площадей плоских фигур можно использовать различные приборы, в частности, палетку. Палетка – это прозрачная пластина, на которой нанесена сеть квадратов. Сторона принимается за1.

Таким образом площадь геометрических фигур можно измерить максимально точно с помощью вычислений, но если фигура произвольна, то ее площадь можно найти только приблизительно.

Математические понятия. Объем и содержание понятия. Определение понятия через род и видовое отличие. Требование к определению понятий

1.Связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др.;

2.Алгебраичкские понятия: выражение, равенство, уравнение и др.;

3.Геометрические понятия: прямая, отрезок, треугольник и т.д.;

4.Понятия, связанные с величинами и их измерением.

Любое математическое понятие характеризуется термином, объемом и содержанием понятия.

Объем понятия – это множество всех объектов, обозначаемых одним термином.

Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.

Понятия обозначаются строчными буквами латинского алфавита: a, b, c, …, z. Их объемы обозначаются соответственно: A, B, C, …, Z.

Если А с В (А = В), то говорят, что понятие а – видовое по отношению к понятию b, а понятие b – родовое по отношению к понятию а.

Если А = В, то говорят, что понятия а и b тождественны (а ≡ b) («равносторонний треугольник» и «равноугольный треугольник»).

В отношении «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок – часть прямой, а не ее вид.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). а b

Определения, имеющие такую структуру называются явными.

Определяемое понятие Родовое понятие + Видовое отличие

Пример: квадрат – прямоугольник, у которого все стороны равны.

Также выделяют неявные понятия, в их структуре нельзя выделить определяемое и определяющее понятия. Среди них различают контекстуальные и остенсивные.

Контекстуальные определения – содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия.

Остенсивные определения – это определения путем показа. Они используются для введения термина путем демонстрации объектов, которые этим термином обозначаются.

Существенное свойство – свойство, присущее этому объекту и без него он не может существовать.

Между объемом и содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот.

Генетические понятия – показ пути зарождения.

Пример: конус – это тело, образованное путем вращения прямоугольного треугольника вокруг одного из катетов.

Индуктивное понятие – определения но основе формулы.

Пример: арифметическая прогрессия – это последовательность чисел, в которой каждый последующий элемент получается путем прибавления одного и того же числа к предыдущему.

Требования к определению понятия:

* определение должно быть соразмерным

* в определении не должно быть порочного круга

* определение должно быть ясным

Дата добавления: 2015-04-18 ; просмотров: 203 ; Нарушение авторских прав

Источник

Формулы площади геометрических фигур.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула Герона

где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b ,
r — радиус вписанной окружности,
R — радиус описанной окружности,

p =	a + b + c	— полупериметр треугольника.
	2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

Формула площади прямоугольника

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Формулы площади ромба

Формулы площади трапеции

Формула Герона для трапеции

S =	a + b	√ ( p-a )( p-b )( p-a-c )( p-a-d )
	| a — b |

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p =	a + b + c + d	— полупериметр трапеции.
	2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d ₁, d ₂ — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.

Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

Формула площади четырехугольника по длине сторон и значению противоположных углов

a , b , c , d — длины сторон четырехугольника,

p = a + b + c + d 2 — полупериметр четырехугольника,

θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади четырехугольника, вокруг которого можно описать окружность

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

Источник