Способы измерения площадей фигур единицы площади

Площадь фигуры. Способы измерения площадей фигур. Равновеликие и равносоставленные фигуры. Нахождение площади прямоугольника

Каждый представляет, что такое площадь комнаты, площадь участка земли. Так же понимает если земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат.

Это обыденное представление о площади. Но когда говорят о площади геометрической фигуры выделяют определённый класс фигур. Например, рассматривают площадь многоугольника, площадь поверхность многоугольника и другое.

Площадью фигуры называется положительная величина определенная для каждой фигуры так, что:

1. Равные фигуры имеют равные площади;

2. Если фигура состоит из двух частей, то ее площадь ровна сумме площадей этих частей.

Чтобы измерить точно площадь фигуры, нужно иметь единицу площади. Такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой Е, а число, которое получается в результате измерения площади – S(F). Это число называют численным значением площади фигуры F при выбранной единице площади E. Оно должно удовлетворять условиям:

1. Число S(F) – положительное.

2. Если фигуры равны, то равны численные значения их площадей.

3. Если F состоит из F1 и F2, то численное значение площади фигуры равно сумме численных значений площадей F1 и F2.

4. При замене единице площади численное значение площади данной фигуры увеличивается (уменьшается) во столько же раз, во сколько новая единица меньше (больше) старой.

5. Численное значение площади единичного квадрата принимается равным 1, т.е. S(F)=1.

6. Если фигура F1 является частью фигуры F2, то численное значение площади фигуры F1 не больше численного значения площади фигуры F2.

Фигуры, у которых площади равны, называются равновеликими.

Многоугольники F1 и F2 называются равносоставленными, если их можно разбить на соответственно равные части.

Любые два равновеликих многоугольника равносоставлены.

Теорема.Площадь прямоугольника равна произведению длин соседних его сторон.

Читайте также: А касательное напряжение (сила, действующая на единицу площади) Агентские сети и способы стимулирования их активности Активные способы проверки домашнего задания Альтернативные способы получения и преобразования энергии. Альтернативные способы получения электрической энергии. Амортизация основных средств, способы начисления амортизационных сумм. Аналоговые каналы передачи данных; способы модуляции, модемы Б7.5 Способы оказания первой помощи пострадавшему при поражения электрическим током. Б8.5 Способы проведения искусственного дыхания и наружного массажа сердца. Бак прямоугольной формы с водой имеет в дне малое отверстие, через которое происходит его опорожнение. Время опорожнения бака _____ раза, если площадь бака увеличить в 4 раза.

E

F Дано:

F – данный прямоугольник

a,b – длины его сторон.

Доказать: S(F) = ab

1. Пусть a и b – натуральные числа. Тогда прямоугольник F можно разбить на единичные квадраты: F = E+E+E…+E. Всего их ab, так как имеем b рядов, в каждом из которых a квадратов. Отсюда S(F)=S(E)+S(E)…+S(E) = abS(E) =ab

Для приближенного измерения площадей плоских фигур можно использовать различные приборы, в частности, палетку. Палетка – это прозрачная пластина, на которой нанесена сеть квадратов. Сторона принимается за1.

Таким образом площадь геометрических фигур можно измерить максимально точно с помощью вычислений, но если фигура произвольна, то ее площадь можно найти только приблизительно.

Математические понятия. Объем и содержание понятия. Определение понятия через род и видовое отличие. Требование к определению понятий

1.Связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др.;

2.Алгебраичкские понятия: выражение, равенство, уравнение и др.;

3.Геометрические понятия: прямая, отрезок, треугольник и т.д.;

4.Понятия, связанные с величинами и их измерением.

Любое математическое понятие характеризуется термином, объемом и содержанием понятия.

Объем понятия – это множество всех объектов, обозначаемых одним термином.

Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.

Понятия обозначаются строчными буквами латинского алфавита: a, b, c, …, z. Их объемы обозначаются соответственно: A, B, C, …, Z.

Если А с В (А = В), то говорят, что понятие а – видовое по отношению к понятию b, а понятие b – родовое по отношению к понятию а.

Если А = В, то говорят, что понятия а и b тождественны (а ≡ b) («равносторонний треугольник» и «равноугольный треугольник»).

В отношении «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок – часть прямой, а не ее вид.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). а b

Определения, имеющие такую структуру называются явными.

Определяемое понятие Родовое понятие + Видовое отличие

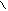
Пример: квадрат – прямоугольник, у которого все стороны равны.

Также выделяют неявные понятия, в их структуре нельзя выделить определяемое и определяющее понятия. Среди них различают контекстуальные и остенсивные.

Контекстуальные определения – содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия.

Остенсивные определения – это определения путем показа. Они используются для введения термина путем демонстрации объектов, которые этим термином обозначаются.

Существенное свойство – свойство, присущее этому объекту и без него он не может существовать.

Между объемом и содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот.

Генетические понятия – показ пути зарождения.

Пример: конус – это тело, образованное путем вращения прямоугольного треугольника вокруг одного из катетов.

Индуктивное понятие – определения но основе формулы.

Пример: арифметическая прогрессия – это последовательность чисел, в которой каждый последующий элемент получается путем прибавления одного и того же числа к предыдущему.

Требования к определению понятия:

* определение должно быть соразмерным

* в определении не должно быть порочного круга

* определение должно быть ясным

Дата добавления: 2015-04-18 ; просмотров: 203 ; Нарушение авторских прав

Источник

Тема урока «Площадь фигуры. Единицы площади». 2-й класс

Класс: 2

Презентация к уроку

Загрузить презентацию (573 кБ)

Цель: познакомиться с понятием площадь фигуры.

Задачи:

• учить находить площадь фигуры с помощью мерки – квадратного сантиметра. Начать систематизировать представления о способах сравнения и измерения площадей; закреплять навыки счёта в пределах 100;
• развивать внимание, логическое мышление, интеллектуальные и коммуникативные общеучебные умения; организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять ошибки;
• воспитывать интерес к изучению математики.

Оборудование: презентация, модели: квадратные сантиметры, квадратные дециметры, квадратные метры.

Этапы урока	Деятельность учителя	Деятельность учащихся
I. Мотивирование к учебной деятельности.

1. Организационный момент. Здравствуй, мой любимый класс,
Очень рада видеть вас!
Ты готов начать урок?
Всё ль на месте?
Всё ль в порядке?
Ручки, книжки и тетрадки? Приветствуют учителя.

Проверяют свою готовность к уроку. II. Актуализация знаний.

Устный счёт. 1)Вставьте пропущенные числа.

2) Решите задачу.

В аллее 28 каштанов, а ясеней в 4 раза меньше. Сколько ясеней растёт в аллее? Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения. III. Определение темы урока.

2. Постановка проблемы. – Как называются данные на доске фигуры?

– Что их объединяет? (Это многоугольники, стороны которых равны 2 см.)

– Как найти периметр каждого многоугольника?

2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см).

2 + 2 + 2 + 2 + 2 = 10 (см).

– Как найти площадь этих фигур?

– Какие трудности у вас возникли?

– Сегодня на уроке мы узнаем, что называют площадью фигуры.

Фиксируют затруднение. IV. Открытие нового знания. Какая фигура меньше занимает места на плоскости?

Говорят, что треугольник имеет меньшую площадь, четырёхугольник.

— Площадь какой фигуры больше?

Площадь – свойство фигуры, занимать место на плоскости.

Площадь – это внутренняя часть фигуры.

— Площадь квадрата больше, чем площадь круга?

— Площадь какой фигуры больше красной или жёлтой?

— Сможем ли мы сравнить площади фигур наложением?

— Наложить мы не сможем эти фигуры, но можем разделить на квадраты и узнать, сколько квадратов занимают фигуры.

Площадь фигуры можно измерять и другими мерками.

Сравните жёлтый и красный прямоугольники по количеству квадратов.

— Сколько квадратов в первом прямоугольнике, во втором?

— Почему так получилось?

Чтобы этого не было вводятся специальные размеры квадратов. Длина стороны квадрата 1 см. Работают с презентацией.

Треугольник занимает меньше места.

Площадь четырёхугольника больше, чем площадь треугольника. Это видно на глаз.

Площадь квадрата больше, чем площадь круга. Проверим способом наложения.

Площадь двух кругов одинаковая.

Сравнивают прямоугольники по количеству квадратов.

Т.к. фигуры разбиты на квадраты разных размеров. V. Первичное закрепление.

Работа в парах. — Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь.

Фигуры у всех разные, но что у них одинаковое?

-Образуйте фигуры, площадь которой 5 кв. см. (4 кв.см) Назовите площадь.

Чтение правила по учебнику стр. 27.

(Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.)

– Сформулируйте определение квадратного метра.

– Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади.

Их обозначают так: см 2 , дм 2 , м 2 .

– Рассмотрите вырезанные из бумаги квадраты площадью 1 дм 2 , 1 см 2 и 1 м 2 .

– Сравните попарно площади этих квадратов.

– В квадрате площадью 1 дм 2 может уместиться ровно 100 квадратов площадью 1 см 2 , а в квадрате площадью 1 м 2 – ровно 100 квадратов площадью 1 дм 2 .

Работают в парах. У учащихся модели 1кв. см.

У наших фигур одинаковые площади.

Читают определение квадратного дециметра, формулируют определение квадратного сантиметра, метра.

Сравнивают попарно площади этих квадратов, накладывая меньший квадрат на больший. Физминутка. Определите площади фигур на экране.

1) Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см 2 .

2) Прямоугольник на рисунке состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см. 1) Фигура состоит из 8 квадратов со стороной 1 см каждый. Значит, площадь всей фигуры равна 8 см 2 .

2) Весь прямоугольник состоит из 5 * 3 = 15 таких квадратов, и его площадь равна 15 см 2 . VI. Самостоятель ная работа. Работа в группах. Дополни высказывание.

• 1 группа. Квадратной единицей называют не квадрат, а его (площадь).
• 2 группа. Квадратным сантиметром называют площадь квадрата с длиной стороны (1 см).
• 3 группа. Квадратным дециметром называют площадь квадрата с длиной стороны (1 дм).
• 4 группа. Квадратным метром называют площадь квадрата с длиной стороны (1 м).

Работают в группах. Дополняют высказывание. VIII. Систематизация и повторение. Задание № 3 (с. 28).

Работа в печатной тетради № 2.

Напиши площадь данных фигур. Читают величины, записанные единицами площади.

Устанавливают взаимосвязь между изученными единицами площади: 1 дм 2 = 100см 2 .

Записывают площадь фигур. VII. Итог урока. Выбери правильное утверждение:

1. Единицы измерения площади:
а) см
б) кв.см
в) кг

2. Площадь – это .
а) сумма длин всех сторон
б) внутренняя часть фигуры
в) всё, что находится вокруг фигуры Что нового узнали на уроке?

– Назовите единицы измерения площади фигуры.

Пригодится ли вам в жизни умение находить площадь фигур?

— Где и зачем?

Выбирают правильное утверждение. Рефлексия деятельности. Покажите своё настроение в конце урока смайликом.

— Что не получилось? Почему?

Литература.

1. В.Н. Рудницкая. Математика: Учебник для 2 класса, рабочая тетрадь № 2 для 2 класса.- М.: Вентана-Граф.
2. Костицын В.Н. Моделирование на уроках геометрии: теория и методические рекомендации. – М.: Владос, 2000.
3. Развитие критического мышления на уроке. Пособие для учителей общеобразовательных учреждений . С. И. Заир-Бек, И. В. Муштавинская. — 2-е изд., М. : Просвещение, 2011.

Источник