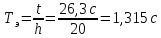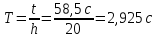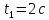Способы измерения момента инерции

1. ЕДИНИЦЫ ИЗМЕРЕНИЯ

Единицей измерения момента инерции вращающейся части I является килограмм-метр в квадрате (кг × м 2 ).

2. МЕТОДЫ ОПРЕДЕЛЕНИЯ МОМЕНТА ИНЕРЦИИ

Для определения момента инерции применяются следующие методы:

2.1. Метод крутильных колебаний

Метод крутильных колебаний следует предпочтительно применять для определения момента инерции вращающихся частей электрических машин мощностью до 100 кВт.

Вращающуюся часть следует подвесить на струне металлической или из иного высокопрочного материала с изотропной структурой согласно черт. 1. Диаметр и длину струны выбирают так, чтобы период крутильных колебаний Т был не менее 1 с. Механическая прочность струны должна соответствовать массе вращающейся части. Точка подвеса должна находиться точно на ее оси вращения.

Вращающуюся часть следует подвергнуть крутильным колебаниям и определить их период Т. При этом одностороннее угловое отклонение должно составлять не более 25°.

Таким же образом и на той же струне следует определить период крутильных колебаний Т_н эталона, момент инерции которого определяют расчетным путем.

Момент инерции исследуемой вращающейся части вычисляют по формуле

где I — момент инерции исследуемой вращающейся части, кг × м 2 ;

I_н — момент инерции эталона, кг × м 2 ;

Т — период колебаний исследуемой вращающейся части, с;

Т_н — период колебаний эталона, с.

Эталон, момент инерции которого определен расчетным путем, может быть также закреплен на валу исследуемой вращающейся части, как показано на черт. 2. В этом случае момент инерции исследуемой вращающейся части следует определять по формуле

где I — момент инерции исследуемой вращающейся части, кг × м 2 ;

I_н — момент инерции эталона, кг × м 2 ;

Т — период колебаний исследуемой вращающейся части, с;

T_н — период колебаний исследуемой вращающейся части с эталоном, с.

Более тяжелые вращающиеся части могут быть подвешены на двух параллельных струнах, прикрепленных к вращающейся части симметрично относительно ее оси в соответствии с черт. 3. Длину струн l и расстояния от струн до оси вращающейся части r следует выбирать таким образом, чтобы период крутильных колебаний Т составлял не менее 1 с.

Вращающуюся часть необходимо подвергнуть крутильным колебаниям и измерить их период Т. Кроме того, надлежит определить массу вращающейся части m. Момент инерции исследуемой вращающейся части вычисляют по формуле

где I — момент инерции исследуемой вращающейся части, кг × м 2 ;

m — масса исследуемой вращающейся части, кг;

r — расстояния от струн до оси вращающейся части, м;

l — длина струн, м;

Т — период крутильных колебаний вращающейся части, с;

g = 9,81 м/с 2 — ускорение земного тяготения.

2.2. Метод вспомогательного маятника

Метод вспомогательного маятника может применяться для определения момента инерции вращающихся частей машин мощностью примерно от 10 до 1000 кВт. Для вращающихся частей, для которых также применим метод крутильных колебаний, последний является предпочтительным.

Вращающуюся часть следует установить на подшипниках балансировочного станка. Вращающиеся части с подшипниками качения могут быть установлены также на собственных подшипниках. Если испытание проводится в собранной машине, то в случае двигателей с фазным ротором и коллекторных машин следует поднять щетки.

Для определения момента инерции методом вспомогательного маятника следует прикрепить к валу исследуемой вращающейся части дополнительную массу m_доп посредством рычага, как показано на черт. 4. Эту массу следует выбрать таким образом, чтобы масса рычага была пренебрежимо малой по сравнению с дополнительной массой m_доп. Дополнительная масса может быть закреплена также на наружной поверхности самой вращающейся части, на шкиве или на полумуфте. Вспомогательный маятник должен быть рассчитан таким образом, чтобы период колебаний Т составлял от 3 до 8 с.

Вращающуюся часть совместно с прикрепленным к ней вспомогательным маятником приводят в колебания. При этом одностороннее угловое отклонение не должно быть более 15°. Период колебаний Т следует определить как средний из нескольких колебаний. Для обеспечения точности измерения периода колебаний его следует производить между моментами прохождения маятника через положение статического равновесия.

Момент инерции испытуемой вращающейся части следует определить по формуле

где m_доп — масса вспомогательного маятника, кг;

а — расстояние от центра тяжести вспомогательного маятника до оси вала вращающейся части, м;

Т — период колебаний маятника, с;

g = 9,81 м/с 2 — ускорение земного тяготения.

Для проверки полученного значения момента инерции опыт необходимо повторить с дополнительной массой другой величины.

Метод самоторможения может применяться для определения момента инерции вращающихся частей электрических машин мощностью свыше 100 кВт. Согласно этому методу машина с испытуемой вращающейся частью приводится во вращение с частотой выше номинальной при номинальном возбуждении или без него и затем отключается от источника питания. Для машин с фазным ротором и коллекторных машин испытание проводится с минимально необходимым количеством щеток, а остальные щетки надлежит поднять. После отключения определяется кривая самоторможения n = f(t) в диапазоне частоты вращения от 1,2n_н до 0,8n_н. Для достижения возможной точности при определении этой кривой снижение частоты вращения следует осциллографировать.

В соответствии с черт. 5 момент инерции I исследуемой вращающейся части для невозбужденной машины следует рассчитать по формуле

а для возбужденной машины по формуле:

где I — момент инерции вращающейся части, кг × м 2 ;

Р_мех — механические потери при номинальной частоте вращения, Вт;

Р_ст — потери в стали при номинальной частоте вращения, Вт;

n _н — номинальная частота вращения, об/мин;

D n — разность между верхним и нижним значениями частоты вращения в опыте, об/мин;

D t — время, в течение которого частота вращения машины изменяется на D n, с;

w _н — номинальная угловая частота вращения, с -1 ;

D w — разность между верхним и нижним значениями угловой частоты вращения, с -1 .

За верхнюю точку частоты вращения принимается наивысшая возможная точка в опыте, но не менее 1,1n_н. Нижняя точка должна отличаться от номинальной на такую же величину частоты вращения.

В случае невозможности повышения частоты вращения сверх номинального значения, вместо номинальной частоты вращения принимается частота вращения, лежащая на участке примерно от 0,9 до 0,8 номинальной частоты вращения. В этом случае потери должны быть измерены на данной частоте вращения.

Если для повышения частоты вращения машина должна быть соединена с приводным двигателем, который невозможно отсоединить на ходу, то в формулах ( 5 ) и (6) под потерями следует понимать потери всего агрегата. Из полученного таким образом момента I следует вычесть момент инерции вращающейся части приводного двигателя и соединительной муфты, подлежащей отдельному определению.

1. Автор — делегация ГДР в Постоянной Комиссии по стандартизации

3. Стандарт СЭВ утвержден на 40-м заседании ПКС

4. Сроки начала применения стандарта СЭВ:

Срок начала применения стандарта СЭВ в договорно-правовых отношениях по экономическому и научно-техническому сотрудничеству

Срок начала применения стандарта СЭВ в народном хозяйстве

Источник

Экспериментальные методы определения моментов инерции.

1) способ качений – используются для тел неправильной формы имеющих отверстия.

Тело подвешивают, определяют его положение центра тяжести, отклоняют из равновесного состояния и приводят в колебательное движение. Экспериментально определяют время τ , n – колебаний и Период Т=τ/n и находят Iz

2)Метод крутильных колебаний

Тело, момент инерции которого необходимо определить, подвешивается на упругом стержне, поворачивается на некоторый угол и отпускается. Начинаются крутильные колебания. Угол закручивания стержня связан с моментом следующим соотношением

=φ K= -частота крутильных колебаний Т=2пи/к

3. способ падающего груза

Метод падающего груза. Недостатком описанных выше двух методов

определения момента инерции ротора является необходимость разборки

двигателя. Метод падающего груза позволяет определить момент инерции

На конце вала или шкива на валу навивают несколько витков гибкого

шнура. Другому концу шнура с прикрепленным к нему грузом дают воз-

можность опускаться (рис. 1.4). При эксперименте измеряют время t, за

которое груз опускается на высоту h. Момент инерции

Источник

Методы определения моментов инерции

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Наименование института – Институт неразрушающего контроля

Наименование направления – Приборостроение

Наименование кафедры – Информационно-измерительная техника

Отчет по лабораторной работе №4

«Методы определения моментов инерции»

Выполнили студенты группы 1Б02: Киселёв Е. К.

Проверил: Гурин Л. Б.

Научиться пользоваться аналитическими и экспериментальными методами определения моментов инерции.

Определение моментов инерции аналитическим методом.

Нарисовать эскиз цилиндрической детали и штангенциркулем снять его размеры. Далее пользуясь методикой и формулой (1) определить момент инерции эталона j. Материал эталона – латунь ЛС -59 ().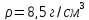

Определение объема цилиндра:

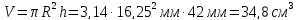
Определение массы цилиндра: =295,8 г

Определение момента инерции:

(1)

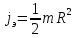
Измерение момента инерции методом крутильных колебаний.

2.1) Закрепить в кронштейне верхнюю втулку торсиона. На нижнем конце торсиона укрепить цилиндрический эталон.

2.2) Сообщить эталону крутильные колебания с амплитудой 20 – 30 градусов и измерить секундомером время 20 – 30 колебаний. Период одного колебания 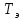находится делением общего времени на число колебаний.

2.3) Снять эталон, установить на его место ротор и аналогичным образом определить период колебаний Т .

2.4) Зная величины Т (с), , рассчитать по формуле (2) момент инерции ротора.

Определение периода колебаний цилиндрического эталона:

Определение периода колебаний ротора:

Определение момента инерции:

(2)

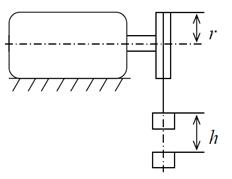
Измерение момента инерции методом падающего груза.

3.1) Установить в кронштейне на место торсиона П – образную рамку с гиромотором. Закрепить на ободе гиромотора конец нити с грузом m. Длина нити должна быть больше расстояния от гиромотора до основания установки. Измерить штангенциркулем радиус гиромотора R.

3.2)Намотав нить на ротор поднять груз до верхнего положения. Измерить расстояние от нижнего края груз до основания установки.

3.3) Опустить груз и одновременно включить секундомер, по которому засечь время t движения груз до момента касания основания. Измерение времени проводить 3 – 5 раз, затем рассчитать среднее значение .

3.4) Используя величины m (кг), R (м), h (м), 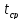(с) рассчитать по формуле (3) момент инерции ротора.

Радиус ротора гиромотора: R=0,027м

Расстояние от нижнего края груза до основания установки: h=0,37м

Масса груза: m=0,005кг

Время движения груза до касания основания:

Расчет момента инерции:

(3)

Измерение момента инерции методом качения ротора с эталоном

4.1) Снять с гиромотора нитку с грузом и укрепить в резьбовом отверстии обода ротора стержень с эталонным грузом m. Измерить расстояние от центра эталона до оси вращения ротора l.

4.2) Отклонить ротор с грузом на небольшой угол (10 – 20 град.) и сообщить ему маятниковые колебания. Секундомером замерить возможно большее количество колебаний (10 – 20 ). Разделив это время на число колебаний найдем период Т одного колебания.

4.3) По формуле (4) рассчитать момент инерции ротора j используя известные величины m (кг), l (м), Т(с)

Масса эталона: m=20гр=0,02кг

Расстояние от центра эталона до оси вращения ротора: l=0,09м

(4)

Измерение момента инерции методом качения физического маятника с эталоном

5.1) Установит стойку с рамкой таким образом, чтобы ось вращения рамки была горизонтальна.

5.2) Измерить с помощью секундомера период маятниковых колебаний рамки.

5.3) Закрепить в верхнем резьбовом отверстии стержень с эталонным грузом. Измерить расстояние l от оси вращения до цента эталона.

5.4) Сообщить системе (рамка + эталон) маятниковые колебания и измерить их период . Амплитуду колебаний нужно задавать примерно такой же как и при качании рамки без эталонного груза.

5.5) Зная величины , (с), m (кг), l (м) рассчитать по формуле (5) момент инерции рамки.

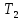
Период маятниковых колебаний рамки: =0,67c

Расстояние от оси вращения до центра эталона: l=0,055м

Период колебания рамки с грузом: 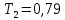с

Масса груза: m=0,02кг

(5)

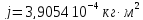
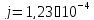
В ходе выполнения работы были рассчитаны моменты инерции различными методами: аналитическим (), крутильных колебаний (), падающего груза (), качения ротора с эталоном (), качения физического маятника с эталоном (j=1,943). Из полученных результатов можно сделать вывод о том, что в каждом из испробованных методов присутствует методическая погрешность. Также причиной того, что результаты получились разные,

Для чего нужно знать моменты инерции?

— Моменты инерции необходимо знать для того чтобы связать между собой и иметь возможность посчитать такие величины как: момент силы, угловую скорость, угловое ускорение, количество оборотов и так далее, все что связано с вращательным движением. Так же момент инерции во вращательном движении, имеет тот же смысл как и масса в поступательном.

От чего зависит погрешность аналитического метода?

— Погрешность аналитического метода зависит от того, что в расчётах момента инерции, присутствует число π, которое является бесконечным десятичным числом. Из-за этого нельзя точно посчитать объём цилиндра и соответственно массу. Что в свою очередь приведёт к небольшой погрешности при расчёте момента инерции.

Какие меры можно предпринять для увеличения точности измерения момента инерции?

— Для точности рекомендуется производить измерения периода колебаний в момент нахождения маятника через положение статического равновесия.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник