Способы измерения масштаба карты

Как определить масштаб топографической карты, измерить по ней расстояние, определить площадь, определить крутизну скатов.

С помощью топографической карты можно решить очень много практических задач, не выходя на местность. По топографической карте можно определить : масштаб данной карты, расстояние между любыми местными предметами, размеры любой площади, крутизну скатов, высоты любых точек местности, взаимное превышение точек, видимость точек, количество деревьев в лесу, количество воды в реке и многое другое.

Как определить масштаб топографической карты, измерить по ней расстояние, определить площадь, определить крутизну скатов.

Обычно на каждой топографической карте дается линейный, численный и текстовой масштаб. Но как быть, если по той или другой причине его не оказалось? Опытный специалист по внешнему виду топографической карты может сразу назвать ее масштаб. Если же вы этого сделать не можете, то следует прибегнуть к следующим способам.

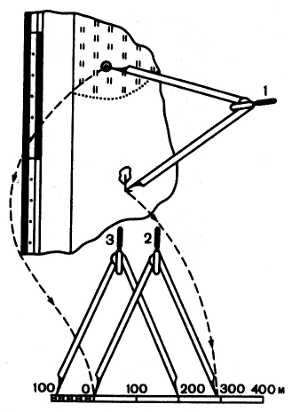
Определение масштаба топографической карты по километровой сетке.

Ее сторона соответствует определенному количеству сантиметров. Если это расстояние равно 2 см, то масштаб карты в 1 см — 500 метров, то есть 1 :50000. Если 4 см, то масштаб карты соответственно будет 1 : 25 000.

Определение масштаба топографической карты по длине дуги меридиана.

Для того чтобы пользоваться этим способом, нужно твердо помнить, что однагеографическая минута по меридиану равна примерно 2 км (точнее 1,85). Подписи градусов и минут имеются на карте, и кроме того, каждая минута выделена шашечкой. Так, например, на рисунке ниже длина одной минуты равна примерно 4 см. Это значит, что масштаб данной карты будет 1:50 000.

Как измерить расстояние по топографической карте.

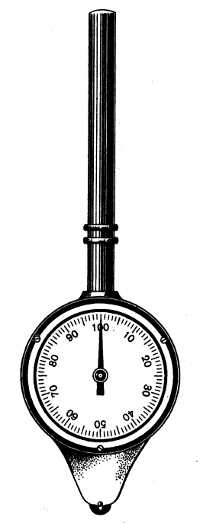
Чтобы определитьрасстояние между двумя точками, вначале измеряют это расстояние на карте, а затем, пользуясь численным или линейным масштабом карты, определяют действительное значение этого расстояния на местности. Если требуется определить расстояние не по прямой, а по извилистой дороге, пользуются специальным прибором — курвиметром.

Это прибор для измерения длины кривых линий. Основанием курвиметра служит колесико, длина окружности которого известна. Вращение колесика передается на стрелку, поворачивающуюся по круговой шкале. Зная число оборотов колесика, катящегося по измеряемой линии, легко определить и ее длину.

Как измерить площадь по топографической карте.

Измерение площади геометрическим способом.

Измеряемая площадь разбивается на сеть треугольников, квадратов, трапеции, площади которых вычисляются по известным формулам. Сумма площадей известных фигур даст общую площадь, заключенную в контуре.

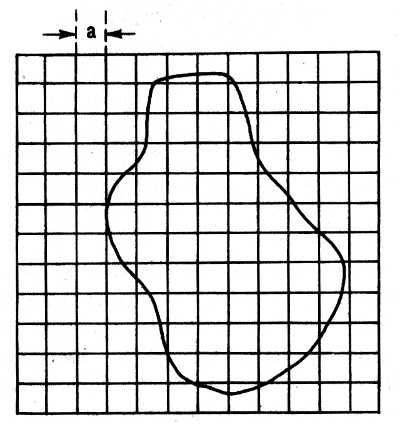
Измерение площади с помощью сетки квадратов.

Очень удобно определять площадь при помощи миллиметровой сетки, которую наносят на прозрачную бумагу или пленку. Такую сетку прикладывают на контур карты и подсчитывают число квадратных миллиметров. Зная, чему равен 1 мм2 топографической карты на местности (для масштаба 1:100 000 — 1 мм2 равен гектару, то есть 100 X 100 м), легко определить площадь на карте.

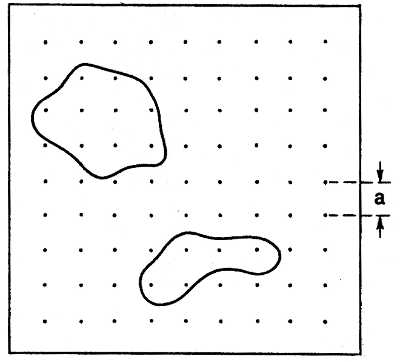
Как определить крутизну скатов по топографической карте.

Расстояние между горизонталями, так называемое заложение, показывает крутизну ската. Основные способы определения крутизны скатов по топографической карте следующие.

Как определить крутизну скатов по шкале заложений топографической карты.

Обычно для определения крутизны скатов на полях топографической карты помещается чертеж — шкала заложений. Вдоль нижнего основания этой шкалы указаны цифры, которые обозначают крутизну скатов в градусах. На перпендикулярах к основанию отложены соответствующие величины заложений в масштабе карты.

В левой части шкала заложений построена для основной высоты сечения, в правой — при пятикратной высоте сечения. Для определения крутизны ската, например, между точками а-в, надо взять циркулем это расстояние и отложить на шкале заложений и прочитать крутизну ската — 3,5 градуса.

Если же требуется определятькрутизну ската между горизонталями утолщенными n-m, то это расстояние надо отложить на правой шкале и крутизна ската в данном случае будет равна 10 градусов.

Как определить крутизну скатов вычислением.

Измерив по карте заложение d и зная высоту сечения h, крутизну ската а можно определить по формуле: а = h/d. Где а — крутизна ската в градусах, d — расстояние между двумя смежными горизонталями в миллиметрах.

Как определить крутизну скатов с помощью линейки или на глаз.

На советскихтопографических картах стандартная высота сечения для каждого масштаба установлена такой, что заложению в 1 см соответствует крутизна около 1 градуса. Из вышеприведенной формулы видно, что во сколько раз заложение меньше одного сантиметра, во столько раз крутизна ската больше одного градуса. Отсюда следует, что заложению в 1 мм соответствует крутизна 10 градусов, заложению в 2 мм — 5 градусов, заложению в 5 мм — 2 градуса и так далее.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

База знаний

§5. МАСШТАБ. ИЗМЕРЕНИЕ РАССТОЯНИЙ И ПЛОЩАДЕЙ ПО КАРТАМ

Масштаб карт. Масштабом топографических карт называется отношение длины линии на карте к длине горизонтальной проекции соответствующей линии местности. На равнинных территориях, при небольших углах наклона физической поверхности, горизонтальные проекции линий весьма мало отличаются от длин самих линий, и в этих случаях можно считать масштабом отношение длины линии на карте к длине соответствующей линии местности, т.е. степень уменьшения длин линий на карте относительно их длины на местности. Масштаб указывается под южной рамкой листа карты в виде отношения чисел (численный масштаб), а также в виде именованного и линейного (графического) масштабов.

Численный масштаб (М) выражается дробью, где в числителе единица, а в знаменателе число, показывающее степень уменьшения: М =1/m . Так, например, на карте в масштабе 1:100 000 длины уменьшены сравнительно с их горизонтальными проекциями (или с действительностью) в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем больше уменьшение длин, тем мельче изображение объектов на карте, т.е. тем мельче масштаб карты.

Именованный масштаб — пояснение, указывающее соотношение длин линий на карте и на местности. При М= 1:100 000 1 см на карте соответствует 1 км.

Линейный масштаб служит для определения по картам длин линий в натуре. Это прямая, разделенная на равные отрезки, соответствующие «круглым» десятичным числам расстояний местности (рис. 5).

Рис. 5. Обозначение масштаба на топографической карте: а — основание линейного масштаба: b — наименьшее деление линейного масштаба; точность масштаба 100 м. Величина масштаба — 1 км

Отрезки a, откладываемые вправо от нуля, называются основанием масштаба. Расстояние на местности, соответствующее основанию, называется величиной линейного масштаба. Для повышения точности определения расстояний крайний слева отрезок линейного масштаба делится на более мелкие части в, называемые наименьшими делениями линейного масштаба. Расстояние на местности, выражаемое одним таким делением, является точностью линейного масштаба. Как видно на рисунке 5, при численном масштабе карты 1:100 000 и основании линейного масштаба в 1 см величина масштаба будет 1 км, а точность масштаба (при наименьшем делении в 1 мм) — 100 м. Точность измерений по картам и точность графических построений на бумаге связаны как с техническими возможностями измерений, так и с разрешающей способностью человеческого зрения. Точность построений на бумаге (графическую точность) принято считать равной 0,2 мм. Разрешающая способность нормального зрения близка к 0,1 мм.

Предельная точность масштаба карты — отрезок на местности, соответствующий 0,1 мм в масштабе данной карты. При масштабе карты 1:100 000 предельная точность составит 10 м, при масштабе 1:10 000 она будет равна 1 м. Очевидно, что возможности изображения на этих картах контуров в их действительных очертаниях будут весьма различны.

Масштабы топографических карт в значительной степени обусловливают отбор и детальность показа изображаемых на них объектов. С уменьшением масштаба, т.е. с увеличением его знаменателя, теряется детальность изображения объектов местности.

Для удовлетворения разнообразных потребностей отраслей народного хозяйства, науки и обороны страны необходимы карты разных масштабов. Для государственных топографических карт СССР разработан ряд стандартных масштабов, основанных на метрической десятичной системе мер (табл. 1).

Таблица 1. Масштабы топографических карт СССР
Численный масштаб	Название карты	1 см на карте соответствует на местности расстоянию	1 см 2 на карте соответ-ствует на местности площади
1:5 000	Пятитысячная	50 м	0,25 га
1:10 000	Десятитысячная	100 м	1 га
1:25 000	Двадцатипятитысячная	250 м	6,25 га
1:50 000	Пятидесятитысячная	500 м	25 га
1:100 000	Стотысячная	1 км	1 км 2
1:200 000	Двухсоттысячная	2 км	4 км 2
1:500 000	Пятисоттысячная	5 км	25 км 2
1:1 000 000	Миллионная	10 км	100 км 2

В комплексе карт, названных в табл. 1, выделяют собственно топографические карты масштабов 1:5000—1:200 000 и обзорно-топографические карты масштабов 1:500 000 и 1:1 000 000. Последние уступают в точности и подробности изображения местности, но отдельные листы охватывают значительные территории, и эти карты используют для общего ознакомления с местностью, для ориентирования при движении с большой скоростью.

Измерение расстояний и площадей по картам. При измерении расстояний по картам следует помнить, что в результате получают длины горизонтальных проекций линий, а не длины линий на земной поверхности. Однако при малых углах наклона разница в длине наклонной линии и ее горизонтальной проекции очень мала и может не учитываться. Так, например, при угле наклона 2° горизонтальная проекция короче самой линии на 0,0006, а при 5° — на 0,0004 ее длины.

При измерении по картам расстояний в горных районах действительное расстояние на наклонной поверхности можно вычислить

по формуле S = d·cos α, где d — длина горизонтальной проекции линии S, α — угол наклона. Углы наклона можно измерить по топографической карте методом, указанным в §11. Поправки в длины наклонных линий приводятся также в таблицах.

Рис. 6. Положение циркуля-измерителя при измерении расстояний по карте с помощью линейного масштаба

Для определения длины отрезка прямой между двумя точками в раствор циркуля-измерителя берут с карты заданный отрезок, переносят на линейный масштаб карты (как указано на рисунке 6) и получают длину линии, выраженную в поземельных мерах (метрах или километрах). Аналогичным образом измеряют длины ломаных линий, беря в раствор циркуля каждый отрезок отдельно и затем суммируя их длины. Измерения расстояний по кривым линиям (по дорогам, границам, рекам и т. п.) более сложны и менее точны. Очень плавные кривые измеряют как ломаные, разбив предварительно на прямолинейные отрезки. Извилистые линии измеряют малым постоянным раствором циркуля, переставляя его («шагая») по всем изгибам линии. Очевидно, что мелкоизвилистые линии следует измерять при весьма малом растворе циркуля (2—4 мм). Зная, какой длине на местности соответствует раствор циркуля, и подсчитав число его установок по всей линии, определяют общую ее длину. При этих измерениях применяют микроизмеритель или пружинный циркуль, раствор которого регулируется винтом, пропущенным через ножки циркуля.

Для измерения кривых линий пользуются также прибором — курвиметром (рис. 7). Находящееся в нижней части прибора колесико катят по измеряемой кривой. Система передач сообщает движение колесика стрелке. По делениям шкалы на циферблате определяют, какое расстояние пройдено колесиком по карте. Полученное расстояние, выраженное в сантиметрах, переводят в натуральную величину. Длины кривых линий, измеренные по карте, меньше истинных величин, так как их изображение всегда несколько обобщено — мелкие извилины объединены или вовсе сглажены.

Рис. 7. Курвиметр

Следует иметь в виду, что любые измерения неизбежно сопровождаются погрешностями (ошибками). По их происхождению ошибки подразделяются на грубые промахи (возникают из-за невнимательности лица, производящего измерения), систематические ошибки (из-за погрешностей мерных приборов и др.), случайные ошибки, которые не могут быть полностью учтены (причины их не ясны). Очевидно, что истинное значение измеряемой величины из-за влияния ошибок измерений остается неизвестным. Поэтому определяют ее вероятнейшее значение. Таким значением является арифметическое среднее из всех отдельных измерений x — (a₁+a₂+ …+а_n):n=∑a/n , где x — вероятнейшее значение измеренной величины, a₁, a₂ … a_n — результаты отдельных измерений; 2 — знак суммы, n — число измерений. Чем больше измерений, тем ближе вероятнейшее значение к истинной величине A. Если предположить, что значение A известно, то разность между этой величиной и измерением а даст истинную погрешность измерения Δ=A—a. Отношение погрешности измерения какой-либо величины A к ее значению называется относительной погрешностью —. Эта погрешность выражается в виде правильной дроби, где в знаменателе — доля ошибки от измеряемой величины, т.е. Δ/A = 1/(A:Δ).

Так, например, при измерении длин кривых курвиметром возникает ошибка измерений порядка 1—2%, т. е. она составит 1/100 — 1/50 часть длины измеряемой линии. Таким образом, при измерении линии длиной 10 см возможна относительная ошибка 1—2 мм. Эта величина в разных масштабах дает разные ошибки в длинах измеряемых линий. Так, на карте масштаба 1:10 000 2 мм соответствует 20 м, а на карте масштаба 1:1 000 000 это будет 200 м. Отсюда следует, что более точные результаты измерений получаются при использовании карт крупных масштабов.

Определение площадей участков по топографическим картам основано на геометрической зависимости между площадью фигуры и ее линейными элементами. Масштаб площадей равен квадрату линейного масштаба. Если стороны прямоугольника на карте уменьшены в n раз, то площадь этой фигуры уменьшится в п2 раз. Для карты масштаба 1:10 000 (1 см — 100 м) масштаб площадей будет равен (1:10 000)2 или 1 см 2 — (100 м) 2 , т.е. в 1 см 2 — 1 га, а на карте масштаба 1:1 000 000 в 1 см 2 — 100 км 2 .

Для измерения площадей по картам применяют графические и инструментальные способы. Применение того или иного способа измерений диктуется формой измеряемого участка, заданной точностью результатов измерений, требуемой быстротой получения данных и наличием необходимых приборов.

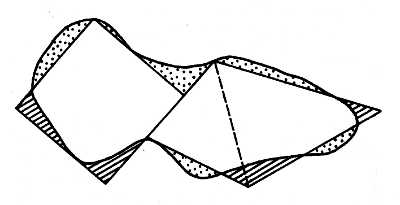
Рис. 8. Спрямление криволинейных границ участка и разбивка его площади на простые геометрические фигуры: точками обозначены отсекаемые участки, штриховкой — причленяемые участки

При измерении площади участка с прямолинейными границами делят участок на простые геометрические фигуры, измеряют площадь каждой из них геометрическим способом и, суммируя площади отдельных участков, вычисленных с учетом масштаба карты, получают общую площадь объекта. Объект с криволинейным контуром разбивают на геометрические фигуры, предварительно спрямив границы с таким расчетом, чтобы сумма отсеченных участков и сумма избытков взаимно компенсировали друг друга (рис. 8). Результаты измерений будут в некоторой степени приближенными.

Рис. 9. Квадратная сеточная палетка, наложенная на измеряемую фигуру. Площадь участка Р=a 2 n, a — сторона квадрата, выраженная в масштабе карты; n — число квадратов, попавших в пределы контура измеряемого участка

Измерение площадей участков, имеющих сложную неправильную конфигурацию, чаще производят с помощью палеток и планиметров, что дает наиболее точные результаты. Сеточная палетка (рис. 9) представляет собой прозрачную пластину (из пластика, органического стекла или кальки) с награвированной или начерченной сеткой квадратов. Палетку накладывают на измеряемый контур и по ней подсчитывают количество клеток и их частей, оказавшихся внутри контура. Доли неполных квадратиков оцениваются на глаз, поэтому для повышения точности измерений применяются палетки с мелкими квадратами (со стороной 2—5 мм). Перед работой на данной карте определяют площадь одной ячейки в поземельных мерах, т.е. цену деления палетки.

Рис. 10. Точечная палетка — видоизмененная квадратная палетка. Р=a 2 n

Помимо сеточных палеток, применяются точечные и параллельные палетки, представляющие собой прозрачные пластины с награвированными точками или линиями. Точки ставятся в одном из углов ячеек сеточной палетки с известной ценой деления, затем линии сетки удаляют (рис. 10). Вес-каждой точки равен цене деления палетки. Площадь измеряемого участка определяется путем подсчета количества точек, оказавшихся внутри контура, и умножением этого количества на вес точки.

Рис. 11. Палетка, состоящая из системы параллельных линий. Площадь фигуры равна сумме длин отрезков (средних пунктирных), отсекаемых контуром участка, умноженной на расстояние между линиями палетки. P = р∑l

На параллельной палетке награвированы равноотстоящие параллельные прямые. Измеряемый участок окажется разделенным на ряд трапеций с одинаковой высотой при наложении на него палетки (рис. 11). Отрезки параллельных линий внутри контура посредине между линиями являются средними линиями трапеций. Измерив все средние линии, умножают их сумму на длину промежутка между линиями и получают площадь всего участка (с учетом площадного масштаба).

Измерение площадей значительных участков производится по картам с помощью планиметра. Наиболее распространенным является полярный планиметр, работа с которым не представляет большой сложности. Однако теория этого прибора довольно сложна и рассматривается в руководствах по геодезии.

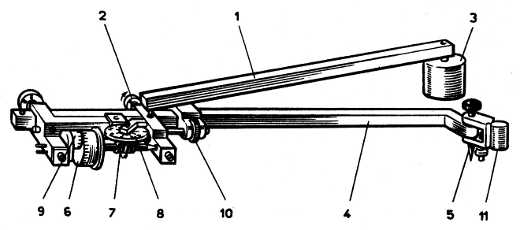
Рис. 12. Полярный планиметр

Прибор имеет два рычага и счетный механизм (рис. 12). Полюсный рычаг 1 соединен шарниром 2 с обводным рычагом 4, а его другой конец опирается на неподвижный полюс 3 — тяжелый цилиндр, снабженный иглой, которая при работе крепит бумагу к столу и обеспечивает неподвижность полюса. Обводный рычаг 4 на одном конце имеет шпиль 5 для обвода измеряемого контура фигуры, а близ другого его конца закреплен счетный механизм. Колесико 6 при движении шпиля катится или скользит по бумаге, его движения передаются червячной передачей 7 на циферблат 8.

Циферблат имеет 10 делений, каждое из которых соответствует одному обороту колесика; на барабане колесика имеется 100 делений для учета части окружности при неполном обороте колесика. По верньеру 9 можно учесть движение колесика с точностью до 1/10 доли наименьшего деления барабана, т.е. до — 1/1000 части его окружности1. Полный отсчет состоит из четырех цифр, которые получают в таком порядке: первую — по циферблату (число оборотов колесика), вторую и третью — по барабану колесика, четвертую — по верньеру. Пример записи отсчета — 3412.

Источник