Измерение длин кривых линий



Циркулярные измерения; способы перехода от длин ломаных к длинам кривых.
На картах крупных и средних масштабов длины прямых и ломаных линий измеряют с помощью циркуля-измерителя и поперечного масштаба с точностью, близкой к предельной для данной карты. Трудности возникают при измерении длин извилистых линий: рек, береговых линий, озёр и морей, контуров, горизонталей.
Универсальным способом считается использование циркуля-измерителя с малыми растворами 1.0; 1.5; 2.0; 4.0 мм. Лучше всего иметь измеритель с микрометренным винтом, который более точно удерживает установленный раствор игл. Измерение выполняется при постоянной величине растворения и заключается в подсчёте числа растворений, укладывающихся по хордам кривой, начиная с точки A.
При последнем уложении циркуль устанавливается так, что бы конец кривой (точка В) находился в створе игл. В этом положении делается отсчёт доли растворения по концу кривой. Измерения в обратном ходе начинаются с точки В. Произведение среднего числа отложений из прямого и обратного ходов на величину растворения даёт длину осреднённой ломаной, вписанной в измеряемую кривую.
Точность определения длин ломаных зависит от длины ломаной, степени извилистости кривой и от величины растворения циркуля.
Установлена закономерность распределения погрешности измерения в зависимости от величины раствора циркуля.
Относительная среднеквадратическая ошибка (ОСКО) измерения подсчитывается по формуле:
n — число отложений циркуля;
– ср.кв. ошибка одного отложения для циркуля с величиной растворения ;
является функцией извилистости кривой и определяется коэффициентом извилистости
— длина ломаной, измерённая циркулем с растворением ( =1,2,3,4 и мм)
Вычислив , по специальной таблице мы по значению получим .
Для получения длин кривых используют разные способы. Рассмотрим 2 из них.
В 1929г. Шокальский предложил способ, суть которого заключается в том, что длина ломаной, измерённая циркулем с растворением 1мм,умноженная на поправочный коэффициент, который мы выбираем, визуально сравнивая измеряемую кривую с кривыми на шкале извилистости. Для этих эталонов установлены значения коэффициентов.
Точность этого способа оценивается относительной среднеквадратической ошибкой около 2.5%.
Второй способ был предложен Волковым, который предложил использовать для измерения кривых 2 циркуля с различными величинами растворений.
Относительная разность длин ломаных , соответствующих , является показателем извилистости кривой
Механический способ определения длин линий.
Для приближённого измерения длин прямых и кривых линий применяются различные курвиметры, непригодные для измерения извилистых линий, т.к. колёсиком курвиметра практически невозможно следить за всеми мелкими извилинами линии, а они и создают длину такой линии.
Путь обводного колёсика a с помощью системы зубчатых передач передаётся на счётный механизм , состоящий из неподвижной стрелки при подвижной шкале (или наоборот).
Прокатывая обводным колёсиком по измеряемой кривой, замечаем отсчёты в начале и конце пути. Разность отсчётов даёт длину кривой в делениях курвиметра.
При измерениях кривых курвиметрами должны соблюдаться следующие условия:
1.Вертикальная ось курвиметра должна быть перпендикулярна плоскости бумаги.
2.Плоскость обводного колёсика должна располагаться по касательной к кривой в каждой её точке.
Но одновременно придавать курвиметру и поступательное и вращательное движение довольно трудно, особенно не точно выполняется вращательное движение.
Был предложен усовершенствованный курвиметр «КС». Здесь диаметр обводного колёсика уменьшен до 3 мм и смещена его ось относительно вертикальной оси стержня, что увеличивает манёвренность курвиметра в отношении поворотов. Исследования показали, что курвиметр «КС» даёт удовлетворительные по точности результаты при измерении кривых с коэффициентом извилистости до 1.11 по шкале извилистости (что соответствует 7-му номеру кривых при 9-ти: №8 -1.21, №9 -1.28).Средние ошибки измерений в таких случаях составляют около 2%.
В основном курвиметр «КС» применяется в системе Гидрометиослужбы.
Общим недостатком описанных курвиметров является то, что обводное колёсико и рука исполнителя закрывают изображение кривой в месте обводки.
Источник
ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ
Линии на топографических картах, длину которых необходимо определить, могут быть:
3. извилистыми (криволинейными).
Измерить расстояние прямых линий между точками можно одним из двух способов:
1. С помощью линейки с миллиметровыми делениями;
2. С помощью численного масштаба.
Для измерения расстояний прямых линий первым способом измеренное на карте расстояние в сантиметрах умножают на знаменатель численного масштаба в метрах. Например, на карте масштаба 1:25 000 расстояние между двумя местными предметами равно 3,6 см; на местности оно будет равно 3,6 * 250 = 900 м.
Для измерения расстояний вторым способом с помощью циркуля – измерителя и линейного масштаба. Циркулем – измерителем берут створ, соответствующий определенному расстоянию на карте, и переносят на линейный масштаб. При этом правая ножка циркуля устанавливается в точку, соответствующая числу километров 0 или 1, а относительно левой снимают отсчет (рис. 9).
Рис. 9. Измерение расстояний с помощью линейного масштаба
Измерение прямолинейных отрезков между точками производят с графической погрешностью 0,1 мм, расхождение между повторными измерениями данного отрезка не должно превышать 0,3 мм.
Измерение ломаных линий производят по частям или путем их последовательного спрямления (способ наращивания). При этом способе (рис. 10) устанавливают ножки измерителя в точках а и б, совмещают край линейки с направлением б–в, вращают измеритель вокруг ножки в точке б и устанавливают вторую ножку измерителя у края линейки в точке а1,т.е. на продолжении отрезка бв. После этого перемещают ножку циркуля из точки б в точку в и получают сумму отрезков аб и бв. Действуя аналогично, получают в растворе циркуля а3д общую длину ломаной линии абвгд.
Рис. 10. Измерение ломаных линий способом наращивания
Для контроля измерения проводят в обратном направлении, от точки д к точке а.
Для измерения извилистых (криволинейных) отрезков применяются специальные приборы – курвиметр (механический и электронный), циркуль-измеритель с постоянным раствором.
Курвиметр механический (рис. 11) состоит из колесика, связанного со стрелкой, которая указывает на циферблате длину линии. Курвиметр имеет две шкалы: метрическую – с пределами измерения от 0 до 100 см, дюймовую — с пределами измерения от 0 до 39,4 дюйма. Удерживая курвиметр перпендикулярно к плоскости карты, ведут его колесико по измеряемому отрезку.
Рис. 11. Курвиметр КУ — А
Перед применением курвиметра необходимо определить цену его деления. Для этого выбирают отрезок известной длины и устанавливают, какое число делений курвиметра п будет соответствовать этому отрезку. Тогда цена деления курвиметра 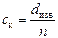
Перед началом измерения отсчет на циферблате курвиметра выводят на 0. Погрешность измерения не превышает 0,25 см на длине измерения 50 см.
Механическим курвиметром объект (реку) необходимо измерить 3 раза (1 — от устья к истоку, 2 — от истока к устью и 3 — от устья к истоку). Например, результаты измерений следующие: n1 – 100см, n2 – 105 см, n3 – 96 см. Если между n1 и n2 5%, то между n2 и n3 уже 9%, такой результат недопустим. Разница между измерениями не должна превышать 5%. Для того чтобы найти истинную длину объекта находят среднюю арифметическую:
Электронный курвиметр Plan Wheel (рис. 12) имеет ЖК-дисплей для вывода результатов измерений. Plan Wheel измеряет расстояния в милях, морских милях и километрах. В приборе можно установить масштаб до 1:10000 для измерений в масштабе картографического материала. Погрешность измерения не превышает 0,2%. Электронным курвиметром объект необходимо измерить 3 раза.
Рис. 12. Электронный курвиметр Plan Wheel
Метод Ю.М. Шокальского.Измеряя некоторые реки азиатской части России циркулями с разными растворами, Ю.М. Шокальский построил графики зависимости полученных длин рек от размеров растворов циркулей – измерителей. Эти графики были использованы для получения поправок на извилистость, значения которых определялись визуально по особо составленной шкале извилистости.
При измерении извилистых линий методом Ю.М. Шокальского линия разбивается на отдельные участки по степени их извилистости. Каждый участок измеряется циркулем с постоянным раствором, равным 1,3 мм. Полученная длина линии по каждому участку умножается на поправочный коэффициент к, соответствующий извилистости измеряемого участка.
Ю.М. Шокальский предложил 5 образцов извилистых линий. В 1961 г. картографическим отделом Государственного гидрологического института (ГГИ) была разработана новая таблица образцов и коэффициентов извилистости к (рис. 13).
Рис.13. Образцы извилистых линий ГГИ. На кривых указаны значения коэффициентов извилистости
Таким образом, методом Ю.М. Шокальского длина извилистой линии может быть определена из выражения
где k — коэффициент извилистости, d — цена раствора циркуля измерителя, n — число отложений циркуля в измеряемой линии.
Метод Н. М. Волкова. Длина Извилистой линии, измеряемой по карте данного масштаба, возрастает по мере уменьшения раствора циркуля. Если отложить на графике по оси абсцисс значения d, а по оси ординат соответствующее значение l, то получим кривую, удовлетворяющую уравнению параболы. При уменьшении размера раствора, в пределе стремящегося к нулю, можно получить действительную, или приведенную, длину lпр линии с учетом всех ее извилин и изгибов.
Измерив одну и ту же линию дважды циркулем с растворами d1 и d2 (d1>d2), получим два значения длины линии — l1 и l2 (l1>l2):

где β – коэффициент, зависящий от извилистости линии,

окончательно приведенная линия длина линии

Метод А. К. Маловичко. Для определения аналитической зависимости между длинами линий l1 и l2, полученными с использованием циркулей с растворами d1 и d2, и приведенной длиной извилистой линии lпр используются правильные геометрические линии. А. К. Маловичко для определения lпр предложил аппроксимировать извилистые линии окружностями. Тогда приведенная длина

где К = (0,5n1–n2)/(n1-n2); n1 и n2 (n2 n2) – число отложений измерителя при определении длин l1 и l2.
Метод Ю. С. Фролова.Дальнейшие изыскания в области определения аналитических зависимостей между длинами, полученными из измерений, и приведенными длинами для правильных геометрических линий привели к использованию для приведения линии, состоящей из сопряженных полуокружностей. В этом случае

Так же, как и в других методах, в методе Ю. С. Фролова выполняются соотношения между ценами делений растворов измерителей d1 l2. Значение коэффициентов k приведены в таблице 4.
| t | k | t | k | t | k | t | k |
| 1,5 | 0,80 | 1,9 | 0,38 | 2,3 | 0,23 | 2,7 | 0,16 |
| 1,6 | 0,64 | 2,0 | 0,33 | 2,4 | 0,21 | 2,8 | 0,15 |
| 1,7 | 0,53 | 2,1 | 0,29 | 2,5 | 0,19 | 2,9 | 0,14 |
| 1,8 | 0,45 | 2,2 | 0,26 | 2,6 | 0,17 | 3,0 | 0,13 |
Редуцированная длина.Вычисленное значение lпр представляет собой длину извилистой линии на карте, от которой необходимо перейти к действительной длине линии в натуре. Исследование закономерности изменения длин извилистых линий с изменением масштабов карт, на которых производятся измерения, показало наличие параболической связи между этими параметрами. Учитывая это, Н. М. Волков предложил определять длину линии на местности как бы в масштабе 1:1.
Приведенная к масштабу 1:1, или редуцированная, длина lред может быть найдена из решения двух уравнений:

где LN1 и LN2 – результаты измерения длин по картам, масштабы которых 1: N1 и 1: N2 (N1
Источник














