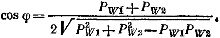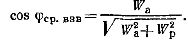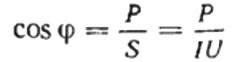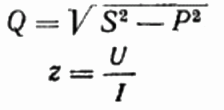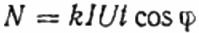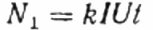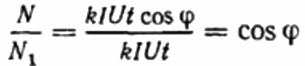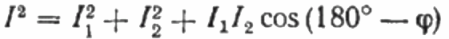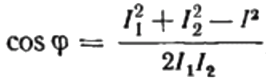Как измерить коэффициент мощности

Для измерения косинус фи лучше всего иметь специальные приборы, предназначенные для непосредственного его измерения — фазометры.

Фазометр — электроизмерительный прибор, предназначенный для измерения углов сдвига фаз между двумя изменяющимися периодически электрическими колебаниями.

Если таких приборов нет, то измерять коэффициент мощности можно косвенным методом . Например, в однофазной сети косинус фи можно определить по показаниям амперметра, вольтметра и ваттметра:

cos фи = P / (U х I), где Р, U, I — показания приборов.

в цепи трехфазного тока cos фи = P w / ( √ 3 х Uл х Iл)

где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.

В симметричной трехфазной цепи значение косинус фи можно определить из показаний двух ваттметров P w 1 и P w 2 по формуле

Общая относительная погрешность рассмотренных методов равна сумме относительных погрешностей каждого прибора, поэтому точность косвенных методов невелика.

Численное значение косинус фи зависит от характера нагрузки. Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит еще и асинхронные электродвигатели, то косинус фи

Поэтому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за сутки или месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле

Это значение средневзвешенного коэффициента мощности желательно иметь в электрических сетях равным 0,92 — 0,95.

Использование фазометра для измерения коэффициента мощности

Измерить непосредственно фазовый сдвиг между напряжением и током нагрузки можно при помощи специальных измерительных приборов — фазометров .

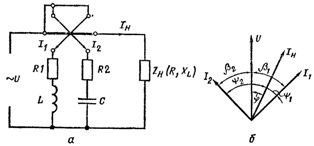
Наибольшее распространение получили фазометры электродинамической системы , в которых неподвижная катушка включена последовательно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток одной из них отстает от напряжения на угол β1. Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2 , для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90 о

Рис. 1. Схема включения фазометра (а) и векторная диаграмма напряжений и токов (б).

Угол отклонения стрелки такого прибора зависит только от значения косинуса фи.

Для измерения фазового сдвига между двумя напряжениями часто применяют цифровые фазометры . В цифровых фазометрах прямого преобразования для измерения фазового сдвига его преобразуют в интервал времени и измеряют последний. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (или в долях градуса).

Из щитовых приборов, предназначенных для измерения, наиболее простой фазометр типа Д31, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.

Для измерения косинуса фи в трехфазной сети при симметричной нагрузке можно применять щитовые фазометры типа Д301. Класс их точности 1,5. Последовательные цепи включают на ток 5 А непосредственно, а также через трансформатор тока, параллельные цепи включают непосредственно на 127, 220, 380 В, а также через измерительные трансформаторы напряжения.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Принцип и способы косвенного определения коэффициента мощности в цепи переменного тока

Коэффициентом мощности или косинусом фи, применительно к потребителю синусоидального переменного тока, называется отношение активной потребляемой мощности P к полной мощности S, которая поставляется к данному потребителю сетью.

Полную мощность S, в общем случае, можно определить как произведение действующих (среднеквадратических) значений тока I и напряжения U в рассматриваемой цепи, а активную мощность P — как безвозвратно расходуемую в потребителе на совершение работы.

Реактивная же мощность Q, хотя и является частью полной мощности, однако на совершение работы она не расходуется, а участвует лишь в создании переменных электрического и магнитного полей в некоторых элементах цепи потребителя.

Кроме непосредственного измерения коэффициента мощности при помощи электродинамических приборов — фазометров, есть вполне логичные косвенные методы, позволяющие математически точно узнать значение этой столь важной электротехнической величины, характеризующей потребитель в цепи синусоидального переменного тока.

Давайте же рассмотрим данные косвенные методы более подробно, разберемся в принципе измерения коэффициента мощности косвенным путем.

Метод вольтметра, амперметра и ваттметра

Электродинамический ваттметр с добавочным активным сопротивлением в цепи своей подвижной катушки показывает величину исключительно активной потребляемой в цепи переменного тока мощности P.

Если теперь с помощью вольтметра и амперметра измерить среднеквадратические значения тока I и напряжения U, действующих в цепи исследуемой нагрузки, то перемножив два данных параметра получим как раз полную мощность S.

Тогда коэффициент мощности (косинус фи) данной нагрузки может быть легко найден с использованием формулы:

Тут же при желании можно найти и величину реактивной мощности Q, полное сопротивление цепи z по закону Ома, а также активное и реактивное сопротивление, просто построив или представив треугольник сопротивлений, а далее воспользовавшись теоремой Пифагора:

Метод счетчика и амперметра

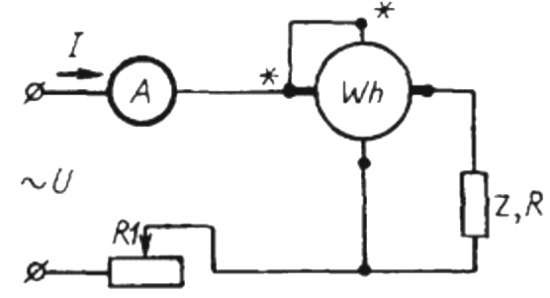
Чтобы воспользоваться данным методом, необходимо собрать схему, в которой последовательно с нагрузкой Z и амперметром подключить простейший счетчик электроэнергии Wh.

За некоторый промежуток времени t, порядка минуты, нужно будет подсчитать количество оборотов диска N, которое покажет количество потребленной за данное время активной энергии (то есть уже с учетом коэффициента мощности).

Здесь: количество оборотов диска N, коэффициент k – количество энергии за оборот, I и U — среднеквадратические ток и напряжение соответственно, t – время счета оборотов, косинус фи — коэффициент мощности:

После этого, вместо исследуемого потребителя Z, через тот же счетчик в цепь включают активную нагрузку R, но не напрямую, а через реостат R1 (добиваясь такого же тока I, что и в первом случае, с потребителем Z). Поддерживают число оборотов диска N1 за аналогичное время t. Но здесь, поскольку нагрузка активная, косинус фи (коэффициент мощности) заведомо равен 1. Поэтому:

Далее записывают отношение оборотов диска счетчика за один и тот же промежуток времени в первом и во втором случае. Это и будет косинус фи, то есть коэффициент мощности первой нагрузки (относительно чисто активной нагрузки с тем же током):

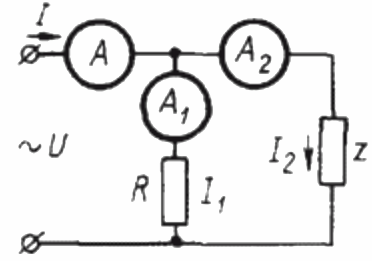
Метод трех амперметров

Для определения коэффициента мощности в цепи синусоидального тока при помощи трех амперметров, прежде всего необходимо собрать следующую цепь:

Здесь Z — потребитель, коэффициент мощности которого необходимо определить, а R – чисто активная нагрузка.

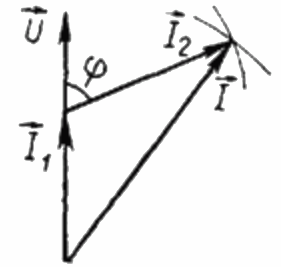
Поскольку нагрузка R чисто активная, то ток I1 в каждый момент времени находится в фазе с приложенным к данному потребителю переменным напряжением U. При этом ток I равен геометрической сумме токов I1 и I2. Теперь построим на основании этого положения векторную диаграмму токов:

На векторной диаграмме токов, острый угол между током I1 и током I2 – есть угол фи, косинус которого (фактически — величину коэффициента мощности) можно найти из специальной таблицы значений тригонометрических функций, либо вычислить по формуле:

Отсюда можно выразить косинус фи, то есть искомый коэффициент мощности:

Знак найденного коэффициента мощности ( «+» или «-») укажет на характер нагрузки. Если коэффициент мощности (косинус фи) получился отрицательным — нагрузка имеет емкостной характер. Если коэффициент мощности — величина положительная — значит характер нагрузки индуктивный.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

ОБОРУДОВАНИЕ
ТЕХНОЛОГИИ
РАЗРАБОТКИ

Блог технической поддержки моих разработок

Коэффициент мощности (cos φ). Понятие, физический смысл, измерение.

Коэффициент мощности (cos φ) это параметр, характеризующий искажения формы тока, потребляемого от электросети переменного тока. Важный показатель потребителя электроэнергии. Во многом он определяет требования к питающей сети. От него зависят потери в проводах и на внутреннем сопротивлении сети.

В цепях постоянного тока мощность, впрочем, как и все остальные параметры, не меняет своего значения в течение определенного отрезка времени. Поэтому, при постоянном токе, существует единственное понятие электрической мощности как произведение значений тока и напряжения.

При переменном токе значения тока и напряжения постоянно меняются с течением времени. Мощность тоже меняется. Поэтому вводится понятие мгновенной мощности.

Мгновенная мощность.

Мгновенная мощность это произведение значения мгновенного напряжения цепи на значение мгновенного тока. На практике мощность связана с выделением тепла, механической работой и т.п. А эти явления имеют инерционный характер. Поэтому понятие мгновенной мощности не имеет практического значения, а используется для расчетов и понимания происходящих процессов.

Действующие значения тока и напряжения.

Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения.

Действующее значение переменного тока определяется как величина такого эквивалентного постоянного тока, который проходя через то же активное сопротивление, что и переменный ток, выделяет на нем за период то же количества тепла. Математически действующее значение определяется как среднеквадратичное за период.

Вольтметры и амперметры переменного тока показывают именно действующие значения. Все операции по тепловым расчетам происходят так же, как и на постоянном токе, только с использованием действующих значений. Но это не всегда правильно.

Полная мощность.

Полная мощность вычисляется как произведение действующих значений тока и напряжения цепи.

В случае синусоидальной формы тока и напряжения, а также отсутствия фазового сдвига, вся полная мощность выделяется на нагрузке. Расчеты для переменного тока соответствуют анализу цепей постоянного тока, только используются действующие значения тока и напряжения.

Полная мощность фактически показывает требования к электрической сети. Измеряется она в В ·А , не в Вт.

Реактивная мощность.

Как только в цепи переменного тока появляются реактивные элементы ( индуктивность и емкость) все меняется. Реактивные элементы обладают способностью накапливать энергию и отдавать ее в цепь обратно. Появляется реактивная мощность.

Реактивная мощность не выделяется на нагрузке, не создает полезной работы. Она накапливается на реактивных элементах нагрузки ( конденсаторах, катушках индуктивности), а затем возвращается обратно в питающую сеть. Понятно, что возвращается она с потерями на проводах, на внутреннем сопротивлении питающей сети и т.п. Поэтому в любой энергосистеме стремятся уменьшить реактивную мощность до минимума.

Реактивная мощность может быть как положительной (для индуктивных цепей), так и отрицательной (для емкостной составляющей).

Единица измерения – вольт-ампер реактивный (ВАР).

Активная мощность.

На нагрузке остается активная мощность. Она и совершает полезную работу. Активная мощность это среднее значение мгновенной мощности за период.

Основные соотношения между параметрами.

Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей.

Активная мощность вычисляется как:

I и U это действующие значения тока и напряжения.

Т.е. активная и полная мощности связаны через коэффициент — cos φ.

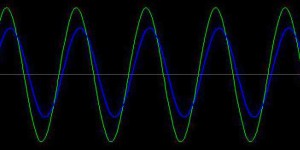
cos φ – это косинус угла сдвига между напряжением питающей сети и током, потребляемым нагрузкой. Это соотношение верно только для синусоидальной формы тока и напряжения. При cos φ = 1 активная мощность на нагрузке равна полной. Вся энергия питающей сети используется для полезной работы. Происходит это только на чисто активной нагрузке, без реактивной составляющей.

cos φ и есть коэффициент мощности (КМ) для переменных цепей с током и напряжением синусоидальной формы.

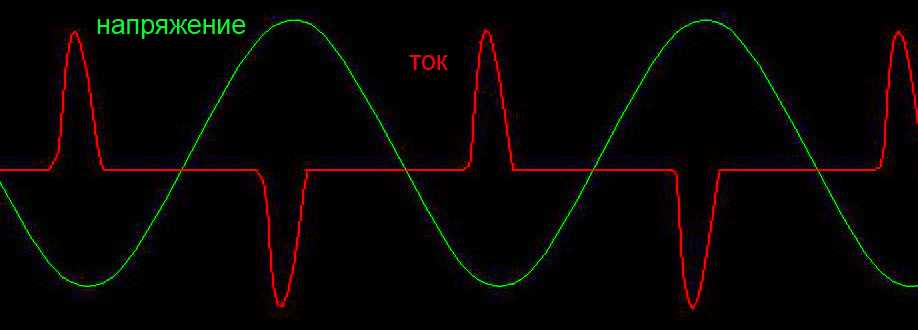
Но многие потребители энергии не только сдвигают фазу, но искажают форму тока. Примером может служить блок питания с бестрансформаторным входом. Это эквивалентная схема подключения его к питающей сети.

В подобных устройствах напряжение питающей сети выпрямляется и сглаживается на конденсаторе большой емкости. Полученное постоянное напряжение с малым уровнем пульсаций используется для дальнейшего преобразования.

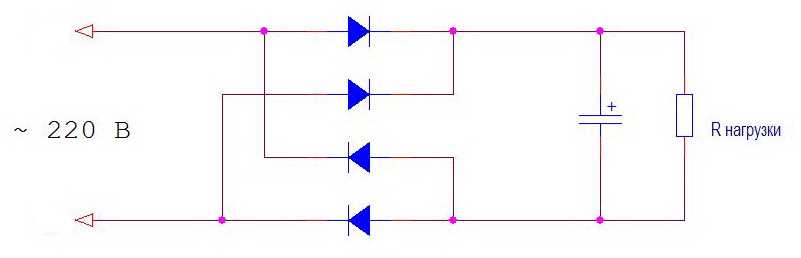
Для питающей сети эта схема представляет нагрузку активно-емкостного характера. Но диоды выпрямительного моста имеют нелинейную характеристику. В начале и в конце периода они закрыты и нагрузка отключена. А в середине периода диоды открываются и кроме активной нагрузки подключают к сети значительную емкость сглаживающего фильтра. В результате ток имеет искаженную форму, показанную на рисунке.

Это один из самых неприятных типов нагрузки, но и самый распространенный. Вся бытовая техника (телевизоры, компьютеры . ) представляют такой характер нагрузки.

Коэффициент мощности (КМ) в переменных цепях с искаженной формой тока определяется как отношение активной мощности к полной.

Следующие диаграммы иллюстрируют, как КМ влияет на работу потребителей электроэнергии.

На этом рисунке показаны осциллограммы чисто активной нагрузки. Фазового сдвига нет, cos φ = 1, вся энергия из сети переходит в активную мощность на нагрузке.

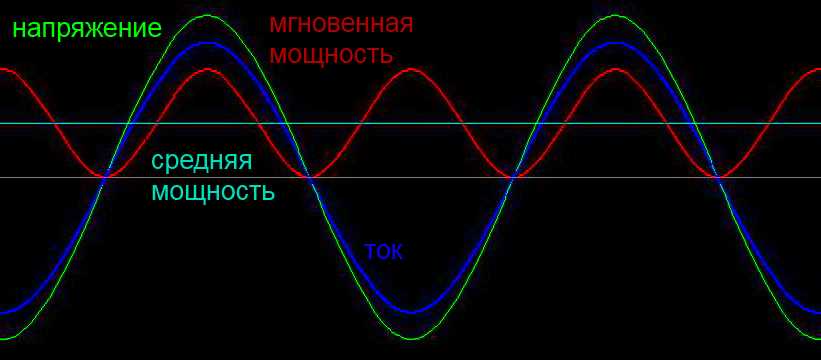
На втором рисунке крайний, самый плохой вариант.

Сдвиг фазы между током и напряжением 90°, cos φ = 0. Видно, что диаграмма мгновенной мощности расположена симметрично относительно 0. Средняя активная мощность равна 0. Конечно, устройств с cos φ = 0 на практике не бывает, но промежуточных вариантов сколько угодно. Например, бестрансформаторный блок питания, приведенный в качестве примера выше, имеет КМ 0,6 — 0,7.

Значимость КМ можно показать простейшими расчетами.

Два потребителя электроэнергии с одинаковой активной (полезной) мощностью. У первого cos φ = 1, а у второго 0,5. Это означает, что второй потребитель потребляет от сети ток в два раза больше, чем первый. Т.к. зависимость потерь в проводах от тока имеет квадратичный характер (P = I 2 * R), то потери на активном сопротивлении проводов во втором случае будут в 4 раза больше. Потребуются провода большего сечения.

Для мощных нагрузок, длинных линий электропередач высокий КМ особенно важен.

Измерение коэффициента мощности.

Для измерения cos φ используются специальные приборы – фазометры. Они применяются в сетях с потребляемым током синусоидальной формы, без искажения.

Для измерения КМ у нагрузок, искажающих ток, обычно пользуются следующей методикой.

Схема измерения коэффициента мощности.

Необходимо вычислить полную мощность, как произведение показаний вольтметра и амперметра.

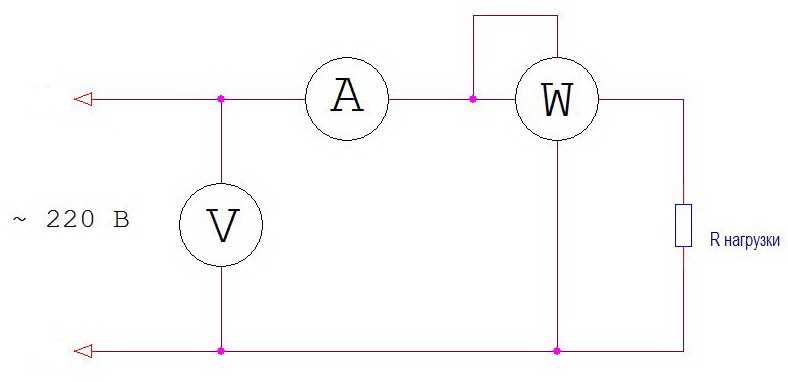
Теперь надо активную мощность (показания ваттметра) разделить на полную.

При отсутствии ваттметра можно использовать счетчик электроэнергии.

Для этого необходимо замерить время 10 калибровочных импульсов (миганий светодиода на корпусе счетчика). Вычислить время периода одного импульса (разделить на 10). Зная коэффициент счетчика (обычно 3200 импульсов на кВт) можно посчитать активную мощность нагрузки. С учетом того, что счетчики электроэнергии имеют класс точности 1.0, измерение получится довольно точным.

Коррекция коэффициента мощности.

Для увеличения КМ существуют специальные устройства – корректоры коэффициента мощности (ККМ). Они бываю пассивными и активными.

Для пассивной коррекции КМ в цепь питания последовательно включают дроссель. Такое решение часто применяется для трансформаторных станций катодной защиты. Но это от безвыходности. Других решений для трансформаторных станций не существует. Дроссель требуется громадных размеров, не меньше чем силовой трансформатор станции. Размеры, вес, цена станции увеличиваются практически в 2 раза, а коэффициент мощности удается поднять только до 0,85.

В инверторных станциях катодной защиты без корректора мощности (выпрямительно-емкостная нагрузка, пример был выше) КМ порядка 0,6 — 0,7. Для его увеличения используют специальные электронные модули – активные корректоры коэффициента мощности. Их схемы, построены по принципу повышающего импульсного преобразователя. Специальные управляющие микросхемы отслеживают форму тока потребления и так управляют ключом преобразователя, что она становится синусоидальной. На выходе активного ККМ формируется постоянное напряжение 380 – 400 В. Поэтому использовать их с трансформаторами невозможно.

Активные корректоры повышают КМ до 0,95 – 0,99.

Пример активного ККМ 2000 Вт для инверторной станции катодной защиты серии «ТИЭЛЛА».

Схемотехнике активных ККМ я посвящу отдельную статью.

Источник