Способы измерения информации энтропийный кибернетический алгоритмический

Методы измерения информации

Как и любое физическое вещество информация имеет свои количественные характеристики. В современной информатике приняты следующие методы измерения информации:

Объемный метод измерения характеризуется количеством символов, содержащихся в конкретном сообщении. В вычислительной технике вся информация, независимо от ее природы (текст, число, изображение и т.д.), представляется в двоичной форме записи, т.е. состоящей из различных комбинаций двух символов 0 и 1. Один такой символ в вычислительной технике называется битом, совокупность восьми таких символов называется байтом, а большое количество символов, которыми оперирует ЭВМ, называется словом.

Энтропийный метод измерения информации используется в теории информации и кодирования. Он основывается на мере неопределенности появления некоторой совокупности событий и выражается вероятностью появления этих событий. Количество информации в сообщении при энтропийном методе оценки определяется тем, насколько уменьшается эта мера после получения сообщения. В теории информации используется следующая количественная мера:

где Э – энтропия;

m – число возможных равновероятных событий.

В случае, когда энтропия зависит не только от числа равновероятных событий выбора, но и от вероятности возможного выбора элемента информации К. Шеннон предложил следующую форму оценки энтропии:

где Р_i – вероятность возможного выбора i-го элемента информации.

Тогда среднее количество информации при m числе выборке с вероятностью Рi каждой выборки определится выражением:

Алгоритмическая оценка информации характеризуется сложностью (размером) алгоритма (программы), которая позволяет ее произвести. На разных машинах и разных языках программирования такая оценка может быть разной. Поэтому задаются некоторой вычислительной машиной (например, элементарной машиной Тьюринга), а предлагаемая количественная оценка информации определяется сложностью слова, как минимальное число внутренних состояний машины, требуемой для его воспроизведения.

Структурная схема машины Тьюринга приведена на рисунке 2.2.

Рисунок 2.2 – Структурная схема машины Тьюринга

На рисунке 2.2 обозначено:

УУ – управляющее устройство;

СГ – считывающая головка;

Лента – источник информации бесконечная лента.

Управляющее устройство УУ определяет положение считывающей головки СГ <q_i>. В каждой ячейке ленты записан символ <a_i>. Таким образом, состояние машины <s_i> определится выражением:

Следующее перемещение ленты задается параметром <p_i>. Тогда новое состояние машины определится следующим образом:

Таким образом, полное состояние машины Тьюринга можно задать, определив множества Q, A, P. Алгоритм определения состояния машины Тьюринга является единицей алгоритмического метода оценки информации.

Источник

Подходы к измерению информации

В информатике используются различные подходы к измерению информации:

Алфавитный (кибернетический, объемный) подход к измерению информациине связывает кол-во информации с содержанием сообщения. Кол-во информации зависит от объема текста и мощности алфавита.

Алфавит – конечное множество различных знаков, символов, для которых определена операция конкатенации (приписывания, присоединения символа к символу или цепочке символов); с ее помощью по определенным правилам соединения символов и слов можно получать слова (цепочки знаков) и словосочетания (цепочки слов) в этом алфавите.

Конечная последовательность букв алфавита называется словом.

Длиной некоторого слова называется число составляющих его символов.

N при алфавитном подходе называют мощностью алфавита. Информационная ёмкость каждого знака зависит от количества знаков в алфавите. Следовательно, каждый из N символов несёт i бит информации.

Остаётся подсчитать количество символов в тексте сообщения k.

Алфавитный подход является объективным способом измерения информации и подходит для работы технических устройств.

Минимальная мощность алфавита, пригодного для передачи информации, равна 2. Такой алфавит называется двоичным алфавитом. Информационный вес символа в двоичном алфавите легко опре­делить. Поскольку 2 i = 2, то i = 1 бит. Итак, один символ двоичного алфавита несет 1 бит информации.

Например, основная физическая единица длины — метр. Но существуют мил­лиметр, сантиметр, километр. Расстояния разного размера удобно выражать через разные единицы. Так же обстоит дело и с измере­нием информации.

1 бит — это исходная единица.

Следующая по величине единица — байт. Байт вводится как информационный вес символа из алфавита мощностью 256. Поскольку 256 = 2 8 , то 1 байт = 8 бит.

Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=2 8 , то 1 символ несет в тексте 8 бит информации.

Пример: слово «мир» несет 24 бит информации.

Содержательный (энтропийный, вероятностный) подход к измерению информации. Этотподход основан на том, что факт получения информации всегда связан с уменьшением неопределенности (энтропии) системы. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Если сообщение не информативно, то количество информации с точки зрения человека = 0.

Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику.

Количество информации — это мера уменьшения неопределенности. В качестве меры неопределенности вводится энтропия Н, а количество информации равно:

I = Hapr – Haps

гдеHapr – априорная энтропия о состоянии исследуемой системы или процесса;

Haps – апостериорная энтропия.

Апостериори (от лат. aposteriori – из последующего) – происходящее из опыта (испытания, измерения). Априори (от лат. apriori – из предшествующего) – понятие, характеризующее знание, предшествующее опыту (испытанию) и независимое от него.

В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, то есть Haps = 0), количество полученной информации совпадает с первоначальной энтропией.

Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N.

Формула Хартли: H= log2N.

Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log₂100 » 6,644. То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.

Приведем другие примеры равновероятных сообщений:

1. при бросании монеты: «выпала решка», «выпал орел»;

2. на странице книги: «количество букв чётное», «количество букв нечётное».

Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.

Формула Шеннона: I = – ( p1 log2 p1 + p2 log2 p2 + . . . + pN log2 pN ), где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. N – количество сообщений

Легко заметить, что если вероятности p₁, . p_N равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.

Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков

1) всего шаров 50+25+25=100

2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4

Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно расcчитать по формуле

Задача2 : В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?

т.к. N = 16 шаров, то I = log2 N = log2 16 = 4 бит.

Алгоритмическое измерение информации [2]

Был предложен в 1965 году академиком А.Н. Колмогоровым. Алгоритмическая сложность некоторой последовательности данных определяется как минимальная длина вычислительного алгоритма, который мог бы воспроизвести заданную последовательность.

Например: слово 000000 – простое, слово 01010101 – более сложное, а слово, в котором 0 и 1 выбираются экспериментально при бросании монеты (1 – орел, 0 – решка), еще сложнее.

Компьютерная программа, печатающая первое слово, совсем простая; для получение второго слова нужна более сложная программа, которая будет печатать символ, противоположный предыдущему. Случайная последовательность, не обладающая никакими закономерностями, может быть напечатана программой, в которой каждый очередной символ будет печататься отдельным оператором. То есть длина такой программы будет близка к длине самой последовательности. Следовательно, любому сообщению можно приписать количественную характеристику, отражающую размер программы, которая позволяет ее воспроизвести.

Источник

Вопрос. Способы измерения информации: сущность технического и энтропийного подходов

Единицы количества информации: кибернетический(энтропийный) и объемный(технический) подходы.

Существуют два основных (и в основе своей разных, хотя и имеющих точки пересечения) подхода к измерению количества информации. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил т.н. кибернетический подход к измерению количества информации, а работы по созданию первых ЭВМ привели к объемному подходу в измерении информации.

Энтропийный подход

Энтропийный способ измерения информации содержащийся в сообщениее

пусть I источник сообщения.

1,2,3. n возможных состояний

pi вероятность состояния любой i (i= от 1 до n)

H= сверху сигмы n сигрма снизу сигмы i=1 pi * log pi по основанию 2

или другими словами

H= log n по основанию 2

Бит (от английского выражения BInary digiTs — двоичные цифры). С точки зрения аппаратной организации компьютера бит, очевидно, является наименьшей возможной единицей информации. Объем же информации в некотором тексте, записанном двоичными знаками в памяти компьютера (или на внешнем носителе информации) подсчитывается чрезвычайно просто, по количеству двоичных символов. При этом, в частности, невозможно нецелое количество битов (в отличие от кибернетического подхода).

Для удобства использования введены более крупные чем бит единицы количества информации. Двоичное слово из восьми знаков (и количество информации, содержащейся в нем) называется байт. 1024 байта образуют килобайт (Кбайт), 1024 килобайта — мегабайт (Мбайт), а 1024 мегабайта — гигабайт (Гбайт).

Между энтропийным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в энтопийном смысле, но заведомо допускает его в объемном.

В информатике принято рассматривать последовательности длиной 8 бит. Такая последовательность называется байтом(1 байт=8 битам).

Байт — это восьмиразрядный двоичный код, с помощью которого можно представить один символ.

С помощью одного байта можно записать двоичные коды 256 (28) чисел от 0 до 255.

Широко используются также еще более крупные производные единицы информации: 1 Килобайт (Кбайт) = 1024 байт = 2 10 байт,1 Мегабайт (Мбайт) = 1024 Кбайт = 2 20 байт,1 Гигабайт (Гбайт) = 1024 Мбайт = 2 30 байт.В последнее время в связи с увеличением объемов обрабатываемой информации входят в употребление такие производные единицы, как: 1 Терабайт (Тбайт) = 1024 Гбайт = 2 40 байт,1 Петабайт (Пбайт) = 1024 Тбайт = 2 50 байт.4 вопрос Информационные процессы: понятие, структура. Взаимосвязь понятий информация и сигнал, информация и данные.(Не уверенна, что всё!)

Информационные процессы

Существуют три вида информационных процессов: хранение, передача, обработка.

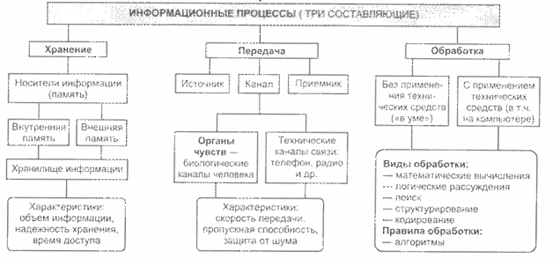
Хранение информации:

· Основные свойства хранилищ информации.

С хранением информации связаны следующие понятия: носи­тель информации (память), внутренняя память, внешняя память, хранилище информации.

Носитель информации – это физическая среда, непосредственно хранящая информацию. Память человека можно назвать опера­тивной памятью. Заученные знания воспроизводятся чело­веком мгновенно. Собственную память мы еще можем назвать внутренней памятью, поскольку ее носитель – мозг – находится внутри нас.

Все прочие виды носителей информации можно назвать вне­шними (по отношению к человеку): дерево, папирус, бумага и т.д. Хранилище информации — это определенным образом организованная информация на внешних носителях, предназначенная для длительного хранения и постоянного использования (например, архивы документов, библиотеки, картотеки). Основной информационной единицей хранилища является определенный физический документ: анкета, книга и др. Под организацией хранилища понимается наличие определенной структуры, т.е. упорядоченность, классификация хранимых документов для удобства работы с ними.

Основные свойства хранилища информации: объем хранимой информации, надежность хранения, время доступа (т.е. время по­иска нужных сведений), наличие защиты информации.

Информацию, хранимую на устройствах компьютерной памя­ти, принято называть данными. Организованные хранилища данных на устройствах внешней памяти компьютера принято называть базами и банками данных.

Обработка информации:

· Общая схема процесса обработки информации.

· Постановка задачи обработки.

· Типовые задачи обработки информации.

Схема обработки информации:

Исходная информация – исполнитель обработки – итоговая информация.

В процессе обработки информации решается некоторая информационная задача, которая предварительно может быть поставлена в традиционной форме: дан некоторый набор исходных данных, требуется получить некоторые результаты. Сам процесс перехода от исходных данных к результату и есть процесс обработки. Объект или субъект, осуществляющий обработку, называют исполнителем обработки.

Для успешного выполнения обработки информации исполнителю (человеку или устройству) должен быть известен алгоритм обработки, т.е. последова­тельность действий, которую нужно выполнить, чтобы достичь нужного результата.

Различают два типа обработки информации. Первый тип обработки: обработка, связанная с получением новой информации, нового содержания знаний (решение математических задач, анализ ситуации и др.). Второй тип обработки: обработка, связанная с изменением фор­мы, но не изменяющая содержания (например, перевод текста с одного языка на другой).

Важным видом обработки информации является кодирование – преобра­зование информации в символьную форму, удобную для ее хра­нения, передачи, обработки. Кодирование активно используется в технических средствах работы с информацией (телеграф, ра­дио, компьютеры). Другой вид обработки информации – структурирование данных (внесение определенного по­рядка в хранилище информации, классификация, каталогизация данных).

Ещё один вид обработки информации – поиск в некотором хранили­ще информации нужных данных, удовлетворяющих определенным условиям поиска (запросу). Алгоритм поиска зависит от способа организации информации.

Передача информации:

· Источник и приемник информации.

· Роль органов чувств в процессе восприятия информации че­ловеком.

· Структура технических систем связи.

· Что такое кодирование и декодирование.

· Понятие шума; приемы защиты от шума.

· Скорость передачи информации и пропускная способность канала.

Схема передачи информации:

Источник информации – информационный канал – приемник информации.

Информация представляется и передается в форме последовательности сигналов, символов. От источника к приёмнику сообщение передается через некоторую материальную среду. Если в процессе передачи ис­пользуются технические средства связи, то их называют каналами передачи информации (информационными каналами). К ним относятся телефон, радио, ТВ. Органы чувств человека исполняют роль биологических информационных каналов.

Процесс передачи информации по техническим каналам связи проходит по следующей схеме:

Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи, прежде всего, возникают по техническим причинам: пло­хое качество линий связи, незащищенность друг от друга различных потоков информации, передаваемой по одним и тем же ка­налам. Для защиты от шума применяются разные способы, например, применение разного рода фильтров, отделяющих полезный сигнал от шума.

5 вопрос. Двоичная форма представления числовых данных (целых и вещественных типов)

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник