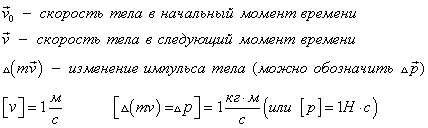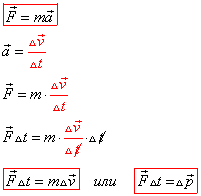Способы измерения импульса силы

Импульс силы — это что такое? Закон силы импульса

Часто в физике говорят об импульсе тела, подразумевая при этом количество движения. На самом же деле это понятие тесно связано с совершенно другой величиной — с силой. Импульс силы — что это, как он вводится в физику, и каков его смысл: все эти вопросы подробно освещены в статье.

Количество движения

Импульс тела и импульс силы — это две взаимосвязанных величины, более того, они практически означают одно и то же. Сначала разберем понятие количества движения.

Количество движения как физическая величина впервые появилось в научных трудах ученых нового времени, в частности в XVII веке. Здесь важно отметить две фигуры: это Галилео Галилей, знаменитый итальянец, который обсуждаемую величину так и называл impeto (импульс), и Исаак Ньютон, великий англичанин, который помимо величины motus (движения) также использовал понятие vis motrix (движущая сила).

Вам будет интересно: Нужно ли высшее образование в наше время: личностное развитие, современные условия приема на работу, советы в построении карьеры

Итак, названные ученые под количеством движения понимали произведение массы объекта на скорость его линейного перемещения в пространстве. Это определение на языке математики записывается так:

Обратим внимание, что речь идет о величине векторной (p¯), направленной в сторону движения тела, которая пропорциональна модулю скорости, а роль коэффициента пропорциональности играет масса тела.

Связь импульса силы и изменения величины p¯

Вам будет интересно: Нужно ли высшее образование в наше время: личностное развитие, современные условия приема на работу, советы в построении карьеры

Как было сказано выше, помимо количества движения Ньютон ввел еще понятие движущей силы. Эту величину он определил так:

Это всем знакомый закон появления ускорения a¯ у тела в результате воздействия на него некоторой внешней силы F¯. Эта важная формула позволяет вывести закон импульса силы. Заметим, что a¯ — это производная по времени скорости (быстрота изменения v¯), что означает следующее:

F¯ = m*dv¯/dt или F¯*dt = m*dv¯ =>

F¯*dt = dp¯, где dp¯ = m*dv¯

Первая формула во второй строке — это импульс силы, то есть величина, равная произведению силы на промежуток времени, в течение которого она действует на тело. Она измеряется в ньютонах на секунду.

Анализ формулы

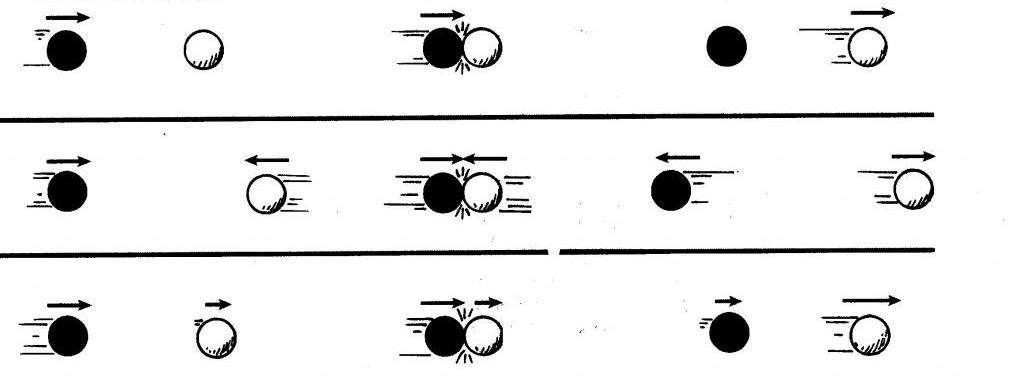
Выражение для импульса силы в предыдущем пункте также раскрывает физический смысл этой величины: она показывает, на сколько изменяется количество движения за промежуток времени dt. Заметим, что это изменение (dp¯) совершенно не зависит от общего значения количества движения тела. Импульс силы — это причина изменения количества движения, которая может приводить как к увеличению последнего (когда угол между силой F¯ и скоростью v¯ меньше 90o), так и к его уменьшению (угол между F¯ и v¯ больше 90o).

Из анализа формулы следует важный вывод: единицы измерения импульса силы совпадают с таковыми для p¯ (ньютон в секунду и килограмм на метр в секунду), более того, первая величина равна изменению второй, поэтому вместо импульса силы часто используют фразу «импульс тела», хотя более правильно говорить «изменение количества движения».

Силы, зависящие и не зависящие от времени

Выше закон импульса силы был представлен в дифференциальной форме. Чтобы посчитать значение этой величины, необходимо провести интегрирование по времени действия. Тогда получаем формулу:

Здесь сила F¯(t) действует на тело в течение времени Δt = t2-t1, что приводит к изменению количества движения на Δp¯. Как видно, импульс силы — это величина, определяемая силой, зависящей от времени.

Теперь рассмотрим более простую ситуацию, которая реализуется в ряде экспериментальных случаев: будем считать, что сила от времени не зависит, тогда можно легко взять интеграл и получить простую формулу:

F¯*∫t1t2 dt = Δp¯ => F¯*(t2-t1) = Δp¯

Последнее равенство позволяет рассчитать импульс постоянной силы.

При решении реальных задач на изменение количества движения, несмотря на то, что сила в общем случае зависит от времени действия, ее полагают постоянной и вычисляют некоторую эффективную среднюю величину F¯.

Примеры проявления на практике импульса силы

Какую роль играет эта величина, проще всего понять на конкретных примерах из практики. Перед тем как их привести, выпишем еще раз соответствующую формулу:

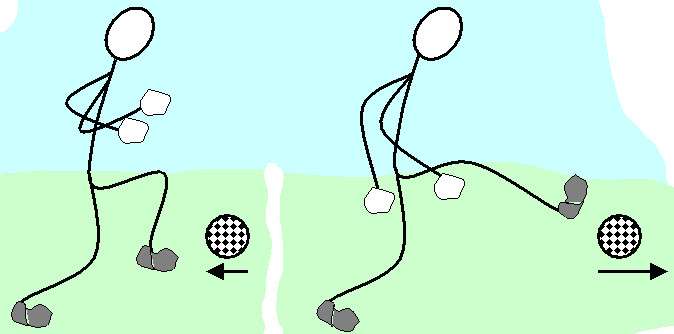
Заметим, если Δp¯ — величина постоянная, тогда модуль импульса силы — это тоже константа, поэтому чем больше Δt, тем меньше F¯, и наоборот.

Теперь приведем конкретные примеры импульса силы в действии:

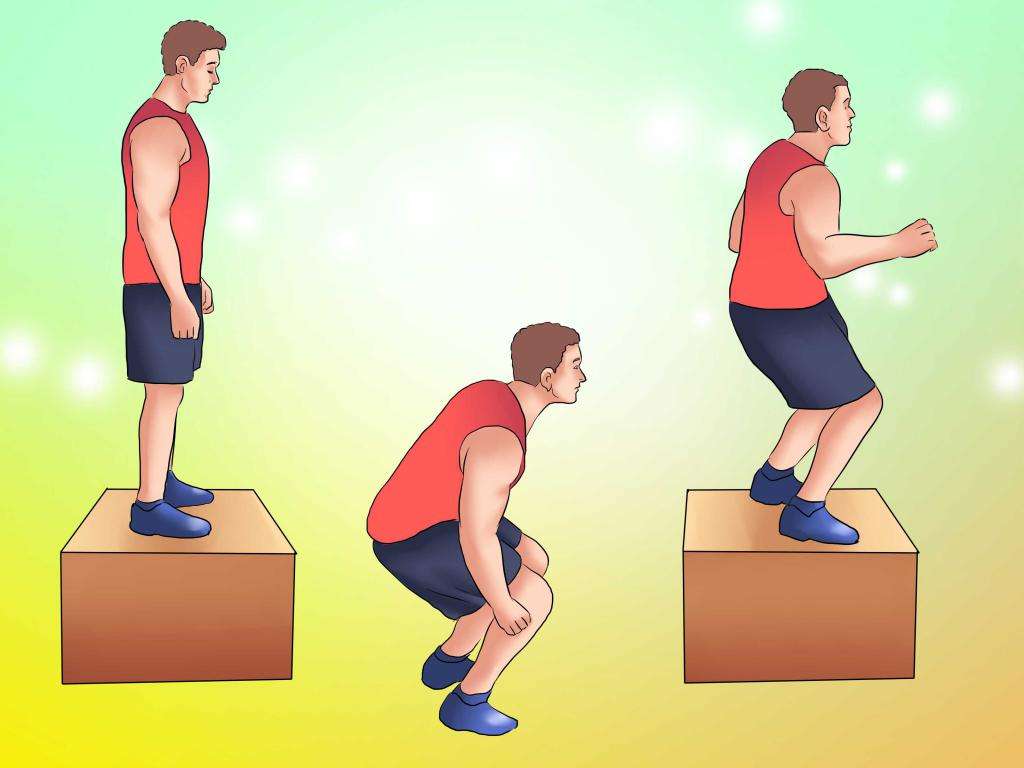
• Человек, который прыгает с любой высоты на землю, старается при приземлении согнуть ноги в коленях, тем самым он увеличивает время Δt воздействия поверхности земли (сила реакции опоры F¯), тем самым уменьшая ее силу.
• Боксер, отклоняя голову от удара, продлевает время контакта Δt перчатки соперника с его лицом, уменьшая ударную силу.
• Современные автомобили стараются конструировать таким образом, чтобы в случае их столкновения их корпус как можно сильнее деформировался (деформация — это процесс, развивающийся во времени, что приводит к значительному снижению силы столкновения и, как следствие, снижению рисков повреждения пассажиров).

Понятие о моменте силы и его импульсе

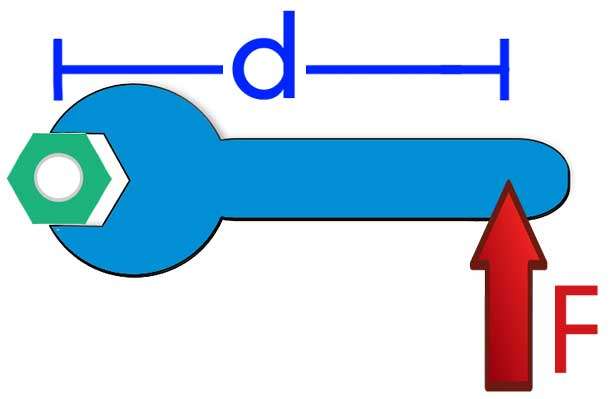
Момент силы и импульс этого момента — это другие величины, отличные от рассмотренной выше, поскольку они касаются уже не линейного, а вращательного движения. Итак, момент силы M¯ определяется как векторное произведение плеча (расстояния от оси вращения до точки воздействия силы) на саму силу, то есть справедлива формула:

Момент силы отражает способность последней выполнить кручение системы вокруг оси. Например, если взяться за гаечный ключ подальше от гайки (большой рычаг d¯), то можно создать большой момент M¯, что позволит открутить гайку.

По аналогии с линейным случаем импульс M¯ можно получить, умножив его на промежуток времени, в течение которого он воздействует на вращающуюся систему, то есть:

Величина ΔL¯ носит название изменения углового момента, или момента импульса. Последнее уравнение имеет важное значение для рассмотрения систем с осью вращения, ведь оно показывает, что момент импульса системы будет сохраняться, если отсутствуют внешние силы, создающие момент M¯, что математически записывается так:

Если M¯= 0, тогда L¯ = const

Таким образом, оба уравнения импульсов (для линейного и кругового движения) оказываются аналогичными в плане их физического смысла и математических следствий.

Задача на столкновение птицы и самолета

Эта проблема не является чем-то фантастическим. Такие столкновения действительно происходят довольно часто. Так, по некоторым данным в 1972 году на территории воздушного пространства Израиля (зона наиболее плотной миграции птиц) было зарегистрировано около 2,5 тысяч столкновений птиц с боевыми и транспортными самолетами, а также с вертолетами.

Задача заключается в следующем: необходимо приблизительно рассчитать, какая сила удара приходится на птицу, если на пути ее движения встречается самолет, летящий со скоростью v=800 км/ч.

Перед тем как приступать к решению, примем, что длина птицы в полете составляет l = 0,5 метра, а ее масса равна m = 4 кг (это может быть, например, селезень или гусь).

Пренебрежем скоростью движения птицы (она мала в сравнении с таковой для самолета), а также будем считать массу самолета намного большей, чем птицы. Эти приближения позволяют говорить, что изменение количества движения птицы равно:

Для вычисления силы удара F необходимо знать продолжительность этого инцидента, она приблизительно равна:

Комбинируя эти две формулы, получаем искомое выражение:

Подставив в него цифры из условия задачи, получаем F = 395062 Н.

Более наглядно будет перевести эту цифру в эквивалентную массу, используя формулу для веса тела. Тогда получим: F = 395062/9,81 ≈ 40 тонн! Иными словами птица воспринимает столкновение с самолетом так, будто на нее свалилось 40 тонн груза.

Источник

Физика. 10 класс

Импульс тела и импульс силы

Импульс. Закон сохранения импульса

Необходимо запомнить

Импульс тела (материальной точки) – это векторная величина, равная произведению массы тела на скорость тела: $\overrightarrow

= m \overrightarrow<\nu>$.

Направление импульса тела всегда совпадает с направлением скорости, т.к. $m > 0$: $\overrightarrow

\uparrow \uparrow \overrightarrow<\nu>$.

Единица измерения импульса : $[p] = \frac<кг \cdot м><с>$.

Импульс силы − произведение силы на время её действия: $\overrightarrow \Delta t$.

Направления $\Delta \overrightarrow

$ и $\overrightarrow$ совпадают, т.к. $\Delta t > 0$.

2-й закон Ньютона в импульсной форме: изменение импульса тела (материальной точки) равно импульсу силы, действующей на него: $\Delta \overrightarrow

= \overrightarrow \Delta t$.

Импульс тела равен сумме импульсов отдельных элементов.

Импульс системы тел равен векторной сумме импульсов каждого из тел системы:

$\overrightarrow

= \overrightarrow + \overrightarrow + . $.

Силы, с которыми взаимодействуют между собой тела системы, называют внутренними, а силы, создаваемые телами, не принадлежащими к данной системе, – внешними.

Систему, на которую не действуют внешние силы, или векторная сумма внешних сил равна нулю, называют замкнутой.

Абсолютно неупругий удар – столкновение тел, в результате которого они соединяются вместе и движутся дальше как одно целое.

Абсолютно упругий удар – столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными.

Закон сохранения импульса:

Векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется при любых взаимодействиях между телами системы: $\sum \overrightarrow

= const$.

Решение задачи на применение закона сохранения импульса

Количество движения

Французский учёный Рене Декарт попытался импульс использовать как величину, заменяющую силу. Потому что силу измерять достаточно сложно, а измерить массу и скорость несложно. Поэтому часто говорят, что импульс – это количество движения (именно Ньютон впервые назвал количеством движения произведение массы тела на скорость).

Декарт, судя по его высказываниям, понимал фундаментальное значение введенного им в XVII веке понятия количества движения – или импульса тела – как произведения массы тела на величину его скорости. И хотя он совершил ошибку, не рассматривая количество движения как векторную величину, сформулированный им закон сохранения количества движения выдержал с честью проверку временем. Ошибка была исправлена в начале XVIII века, и триумфальное шествие этого закона в науке и технике продолжается по сию пору.

Как один из фундаментальных законов физики, он дал неоценимое орудие исследования учёным, ставя запрет одним процессам и открывая дорогу другим. Везде превосходно работает этот закон – реактивное движение, атомные и ядерные превращения, взрыв. А в скольких самых обиходных ситуациях помогает разобраться понятие импульса.

. Декарт обосновывал принцип сохранения количества движения совершенством бога, «действующего с величайшим постоянством и неизменностью».

. закон сохранения импульса позволяет «разыскать» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.

Источник

I. Механика

Тестирование онлайн

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Источник