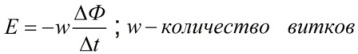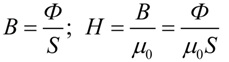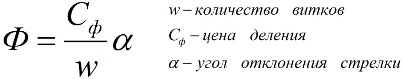Измерение магнитной индукции и напряженности магнитного поля

Приборы для измерения магнитной индукции и напряженности магнитного поля (далее — МП) называются тесламетрами (Тм), по аналогии с измеряемой величиной. Процесс измерения магнитных величин более сложный, чем определение электрических величин, соответственно и приборы и схемы тоже сложнее.

Наиболее распространенными магнитоизмерительными приборами для определения индукции и напряженности являются: Тм с преобразователем Холла, ферромодуляционный и ядерно-резонансный тесламетр.

Тм с преобразователем Холла определяют параметры средних (от 10-5 до 10-1 Тл) и сильных (10-1 до102 Тл) МП. Принцип работы таких тесламетров основан на появлении ЭДС в полупроводниках, помещенных в зону влияния МП.

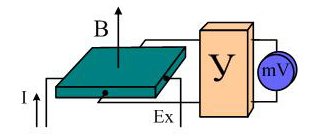
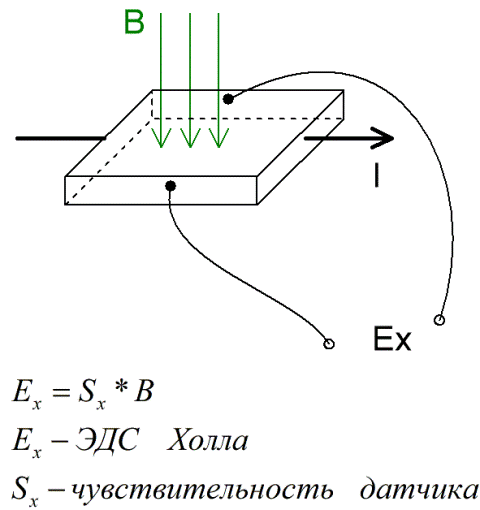
При этом вектор магнитной индукции искомого МП должен быть перпендикулярен пластине полупроводника.

Через тело полупроводника протекает электрический ток I. В результате на боковых гранях пластины образуется разность потенциалов, которую называют ЭДС Холла. ЭДС определяется компенсационным методом или милливольтметром, шкала которого градуирована в теслах. На практике ЭДС Холла зависит от следующих параметров:

где С – коэффициент, учитывающий конструктивные параметры пластины полупроводника; I – сила тока, А; В – магнитная индукция, Тл.

Зная силу тока I, коэффициент С и значение Ех, прибор градуируют в единицах измерения МП, при условии, что сила тока постоянна.

Тм с преобразователем Холла просты в применении, имеют небольшие размеры, что позволяет применять их при измерениях в малых зазорах. С их помощью определяют параметры постоянных, переменных и импульсных полей.

Пределы измерения обычного прибора от 2*10-3 до 2 Тл, с относительной погрешностью ±1,5–2,5%.

Вторым видом приборов для определения характеристик МП является ферромодуляционный тесламетр (ФМТ). Используют ФМТ для измерения слабых и средних, постоянных и переменных (до 1кГц) МП.

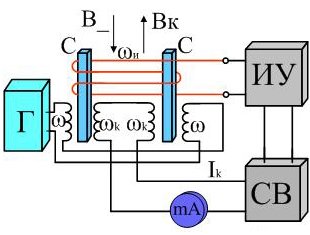
В основу работы ФМТ заложено свойство пермаллоевых сердечников С, изменять свое магнитное состояние, при одновременном воздействии на них постоянного и переменного МП.

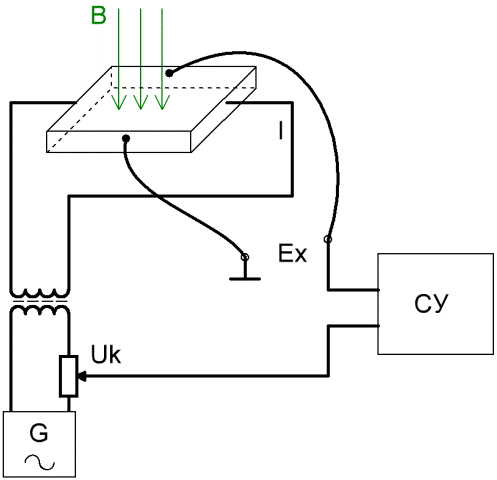
Наиболее широкое применение в схеме измерения рис.2 нашли дифференциальные ферромодуляционные преобразователи. Генератор Г служит для создания переменного МП, которое посредствам катушек ω влияет на сердечники С.

В связи с тем, что эти катушки включены встречно, т. е. конец одной совпадает с другой, ЭДС в цепи индикаторной катушки ωи отсутствует.

Если внести сердечники С в постоянное МП (измеряемое поле), так чтобы вектор магнитной индукции был параллелен оси сердечников, в измерительной обмотке появится ЭДС. Это явление происходит благодаря физическим свойствам пермаллоя, изменять свое магнитное состояние под воздействием двух разнородных полей.

Итак, под влиянием поля В_ , на входе избирательного усилителя ИУ, на ряду с нечетными гармониками, появятся четные. В частности ЭДС второй гармоники имеет прямую зависимость от напряженности МП Н и магнитной индукции В_.

где k и k1 – коэффициенты, учитывающие конструкционные особенности сердечников, частоту и напряженность поля возбуждения ω; Н – измеряемая напряженность МП; В_ — измеряемая индукция.

Синхронный выпрямитель получает с выхода ИУ усиленный сигнал ЭДС второй гармоники, преобразует ЭДС в пропорциональный ей (а значит и Н и В_) ток компенсации Iк.

Ток компенсации, протекая по компенсирующим обмоткам ωк, создает компенсирующее поле Вк, которое стремится уравновеситься с В_, и имеет встречное направление. Миллиамперметр, по которому также протекает ток Iк, градуирован в теслах.

Ферромодуляционные тесламетры имеют высокую чувствительность, точность, и могут быть использованы для непрерывных измерений параметров магнитного поля. Пределы измерения ФМТ от 10-6 до 1 мТл, с погрешностью от 1 до 5%.

Тесламетры с квантовыми магнитоизмерительными преобразователями используют для измерения средних и слабых МП, постоянных и переменных частотой до 20 кГц полей. Принцип действия квантовых магнитоизмерительных преобразователей заключается во взаимодействии ядер молекул вещества с МП.

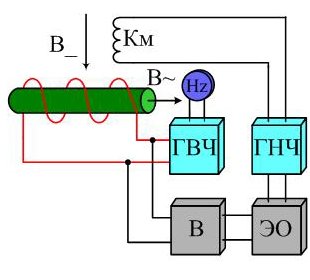
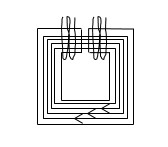
На рис.3 представлена схема распространенного ядерно-резонансного преобразователя. В колбе находится рабочее вещество. По средствам генератора высокой частоты ГВЧ и катушки, охватывающей витками колбу, к рабочему веществу приложено переменное МП.

Взаимодействие ядер с МП называется прецессией. Итак, в колбе частицы прецессируют вокруг вектора магнитной индукции переменного поля.

Под прямым углом, на колбу с рабочим веществом, начинает действовать измеряемое постоянное МП В_. Плавно изменяя частоту переменного поля, добиваются ядерного магнитного резонанса – совпадения частоты прецессии с частотой переменного поля. Резонанс заключается в увеличении амплитуды прецессии.

Этот процесс сопровождается поглощением части энергии переменного ВЧ поля, что приводит к изменению добротности катушки, а соответственно и изменению напряжения на ее концах.

Явление резонанса можно наблюдать на экране электронного осциллографа ЭО, на горизонтальный вход которого подается напряжение ГНЧ, а на вертикальный – выпрямленное напряжение рабочей катушки. ГНЧ питает током низкой частоты катушку модуляции Км, которая служит для модуляции магнитной индукции В_.

Ядерно-резонансные тесламетры являются самыми точными, их относительная погрешность составляет 0,001–0,1%, в области значений 10-2–10 Тл.

Источник

Средства и методы измерения магнитных величин

Иногда, для решения технических задач или в исследовательских целях, возникает потребность в измерении магнитных величин. Безусловно, значение требуемой магнитной величины можно найти и косвенным путем, прибегнув к формулам с опорой на известные исходные данные. Однако, для получения наиболее точного значения магнитного потока Ф, магнитной индукции B или напряженности магнитного поля H лучше подойдет метод прямого измерения. Давайте же рассмотрим методы прямого измерения магнитных величин.

Принципиально метод измерения магнитной величины может быть основан на действии магнитного поля на ток или на проводник. Сила, вызываемая магнитным полем, связывается с электрическим процессом, и затем, посредством электроизмерительного прибора, получается значение измеряемой величины в удобном для человеческого восприятия виде.

Основных методов измерения магнитных величин два: индукционный и гальваномагнитный.

Первый основан на наведении ЭДС при изменении магнитного потока, второй — на действии магнитного поля на ток. Рассмотрим два этих метода по отдельности.

Метод электромагнитной индукции

Известно, что при пересечении витков катушки L магнитным потоком Ф (при изменении магнитного протока, пронизывающего контур) в проводе катушки индуцируется ЭДС (E), пропорциональная скорости изменения магнитного потока dФ/dt, то есть пропорциональная и его величине Ф. Данное явление описывается формулой:

При однородном магнитном поле магнитный поток Ф будет прямопропорционален магнитной индукции B, а коэффициентом пропорциональности будет площадь контура S, пронизываемого линиями магнитной индукции.

Далее — магнитная индукция B окажется прямопропорциональна напряженности магнитного поля H через магнитную постоянную μ0, если явление происходит в ваккууме, либо с учетом магнитной проницаемости среды — еще и через относительную магнитную проницаемость μ этой среды.

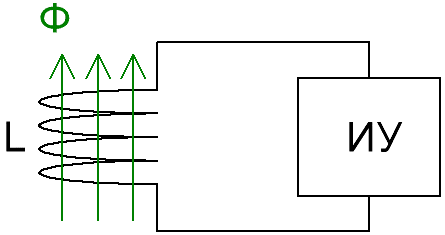
Так, индукционный метод позволяет найти значения: магнитного потока Ф, магнитной индукции B и напряженности магнитного поля H. Приборы для измерения магнитного потока называются веберметрами или флюксметрами (от flux – поток).

Веберметр состоит из индукционной катушки с заранее известными параметрами и интегрирующего устройства ИУ. Интегрирующее устройство представляет собой магнитоэлектрический гальванометр.

Если катушку веберметра вносить или выносить из пространства, где присутствует магнитное поле, то отклонение измерительного механизма веберметра (отклонение стрелки или изменение цифр на дисплее) будет пропорционально индукции B этого магнитного поля. Математическая зависимость легко описывается формулой:

Гальваномагнитный метод (метод Холла)

Общеизвестно, что на проводник с током, находящийся во внешнем магнитном поле, действует сила Ампера, а если рассмотреть процесс более щепетильно, то на движущиеся внутри проводника заряженные частицы действует сила Лоренца.

Так, если проводящую пластину поместить в магнитное поле, и пропустить через пластину постоянный или переменный электрический ток, то на краях пластины возникнет постоянная или переменная разность потенциалов. Эта разность потенциалов Ех называется ЭДС Холла.

Исходя из известных параметров пластины, зная ЭДС Холла, можно определить значение магнитной индукции B. Устройство, предназначенное для измерения магнитной индукции называется тесламетром.

Если преобразователь Холла (датчик Холла) запитать от одного источника, а затем подать компенсирующую разность потенциалов от второго источника, то можно компенсационным методом при помощи сравнивающего устройства определить ЭДС Холла.

Устройство довольно просто: компенсирующее напряжение, снимаемое с регулируемого резистора, подают в противофазе с ЭДС Холла, и так определяют значение ЭДС Холла. Когда компенсационная цепь и датчик Холла питаются от одного источника, то исключается погрешность, могущая возникнуть от нестабильности напряжения и частоты генератора.

Датчики Холла широко применяют в качестве датчиков положения ротора в электродвигателях и в других машинах, где можно получать сигнал от перемещающегося постоянного магнита или от намагничиваемого сердечника трансформатора. В частности, датчик Холла в некоторых применениях выступает своеобразной альтернативой измерительному трансформатору тока.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках

Прямое измерение индукции магнитного поля

Прямое измерение индукции магнитного поля при помощи витка с током основано на явлении электромагнитной индукции Фарадея.

Напомним один из основных законов электромагнетизма.

Закон электромагнитной индукции Фарадея

При изменении магнитного потока, проходящего через замкнутый контур, в контуре возникает ЭДС индукции.

Скорость изменения магнитного потока через замкнутый контур по модулю равна ЭДС индукции, возникающей в контуре.

Как измерить индукцию магнитного поля прямым методом? Сначала проводник в виде небольшой плоской петли замыкают на гальванометр и ориентируют так, чтобы линии магнитной индукции магнитного поля были перпендикулярны плоскости проводника. Затем проводник поворачивают вокруг своей оси на 90 ° . По закону электромагнитной индукции через гальванометр при этом должен пройти импульс тока. Измерив этот импульс, определяют среднее значение магнитной индукции B в области петли.

Косвенные методы измерение напряженности и индукции магнитного поля

Прямое (непосредственное) измерение величины B описанным выше способом возможно не всегда. Например, так невозможно измерить индукцию магнитного поля в веществе.

Необходимо принимать во внимание, что при переходе границы магнетика нормальные составляющие вектора магнитной индукции и тангенциальные составляющие вектора напряженности непрерывны.

Как измеряют вектор магнитной индукции в веществе? Для этого в исследуемом материале делают полость и проводят измерение. Также при обработке результатов учитывают форму полости.

Способ 1. В магнетике делают параллельный магнитному полю и бесконечно узкий канал. Так как канал бесконечно узкий, можно принять, что напряженность поля в нем и в окружающем магнетике одинаковы. В канал помещается пробный виток, измеряется величина магнитной индукции. Так как в канале отсутствует вещество магнетика и μ = 1 , получаем:

Способ 2. В магнетике создают бесконечно узкую щель. Удаление вещества, учитывая бесконечно малый размер щели, не сказывается на магнитном поле (удалением вещества можно пренебречь). Измеряя индукцию в щели, узнаем индукцию магнитного поля в веществе.

Пусть у нас есть электромагнит, состоящий из железного сердечника и катушек с током. Число витков с током равно N . Сердечник имеет узкий воздушный зазор длиной l v . По большей части линии магнитной индукции сосредоточены внутри сердечника и пересекают границу воздух-сердечник по нормали к поверхности раздела. Найти величину магнитной индукции в воздушном зазоре электромагнита.

Магнитная индукция в зазоре и сердечнике одинакова по модулю, если зазор бесконечно мал.

Применяя теорему о циркуляции вектора напряженности H → , получим выражения для напряженности в железе и воздухе.

Напряженность в железе равна H F e = B μ 0 μ F e . Напряженность в воздухе: H v = B μ 0 μ v . Циркуляция вектора напряженности запишется в виде:

H F e l F e + H v l v = N I

где I — сила тока в катушке, l F e — длина контура в железном сердечнике.

Подставим сюда записанные выше выражение для напряженности:

B μ 0 μ F e l F e + B μ 0 μ v l v = N I .

Отсюда выразим магнитную индукцию:

B = μ 0 l N l v μ v + l F e μ F e ≈ μ 0 l N l v + l F e μ F e .

Магнитная проницаемость железа велика, и соотношением l F e μ F e ≪ 1 можно пренебречь. Тогда выражение для индукции запишется в виде:

Измерение напряженности магнитного поля методом Гаусса

Данный метод применяется для измерения магнитного поля Земли.

Постоянные магниты — это магнетики, вектор намагниченности J → которых остается неизменным (или меняется незначительно) при внесении магнетика во внешнее магнитное поле.

На этом определении и базируется суть метода. Для измерения напряженности магнитного поля методом Гаусса берется постоянный магнит в форме стержня, намагниченный параллельно оси. Если поместить такой магнит в постоянное магнитное поле с индукцией B → , на него будет действовать вращающий магнитный момент M → .

Здесь P m → — магнитный момент стержня. Под действием момента M → стержень, вращаясь вокруг своего центра масс, придет в состояние равновесия и установится вдоль вектора поля B → . При небольших отклонениях от положения равновесия возникают колебания с периодом T = 2 π θ P m → B → , где θ — момент инерции стержня.

Магнит-стержень закрепляется перпендикулярно магнитному полю B → , а на расстоянии r от его центра помещается маленькая магнитная стрелка. Стержень можно считать магнитным диполем, а для магнитного поля стержня в месте нахождения стрелки можно записать:

Под воздействием полей B → и B → 1 стрелка установится под углом α к постоянному магнитному полю:

t g α = B 1 B = 2 P m B r 3 .

Измеряя период T и вычисляя угол α , находят магнитный момент стержня и значение индукции магнитного поля.

Источник