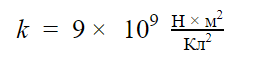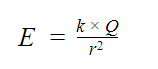Способы измерения электрического поля

Напряженность электрического поля

О чем эта статья:

8 класс, 10 класс

Что такое электрическое поле

Однажды Бенджамин Франклин, чей портрет можно увидеть на стодолларовой купюре, запускал воздушного змея во время дождя с грозой. Столь странное занятие он выбрал не просто так, а с целью исследования природы молнии. Заметив, что на промокшем шнуре волоски поднялись вверх (т. е. он наэлектризовался), Франклин хотел прикоснуться к металлическому ключу. Но стоило ему приблизить палец, раздался характерный треск и появились искры. Сработало электрическое поле.

Это случилось в середине XVIII века, но еще целое столетие ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает между заряженными телами и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Объекты, несущие одноименные заряды, будут отталкиваться, а тела с разноименными зарядами — притягиваться.

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

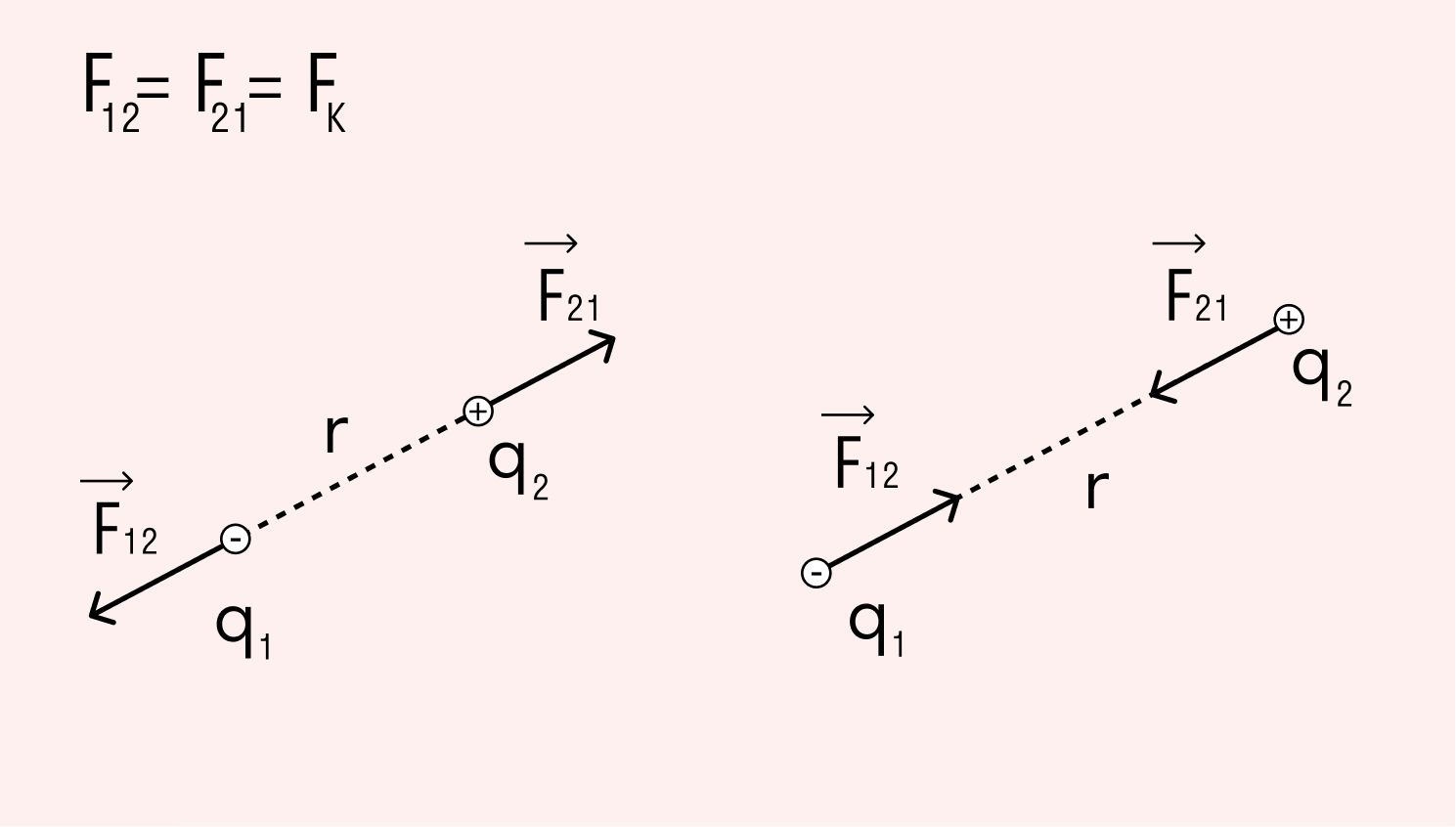
Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление, то есть вектор.

Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые объекты.

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

F = q × E

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые перекрестно взаимодействуют и образуют общее поле. Чему равна напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав напряжения, создаваемые каждым зарядом в отдельности в той же точке (с учетом вектора). Это и есть принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

расстояние между зарядами очень мало — порядка 10 -15 м;

речь идет о сверхсильных полях с напряженностью более 10 20 в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряженных тела, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на эти объекты воздействуют силы, направленные по соединяющей их прямой.

Закон Кулона

Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: 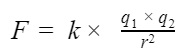где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Линии напряженности

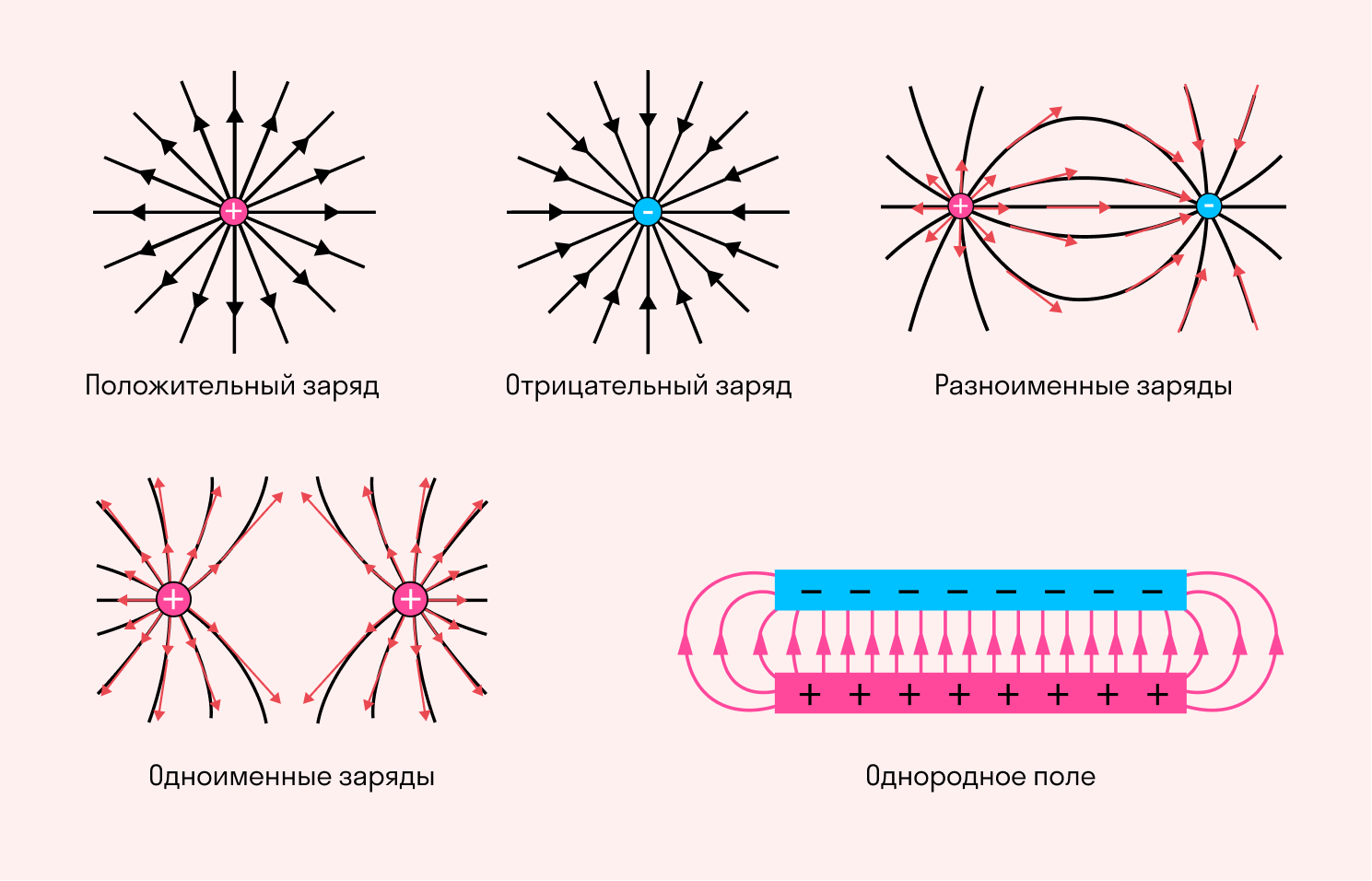
Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Источник

Принципиальные методы измерения напряженности

Способом измерить напряженность электрического поля является принципиальный способ измерения векторов E → и D → , основанный на граничных условиях для данных векторов при переходе поля через границу двух диэлектриков.

Обычный метод измерения напряженности

Стоит заметить, что за обычный принимают метод измерения напряженности поля по силе, воздействующей на пробный заряд, который помещен в поле. Но такой способ возможно применять и для поля в вакууме, при этом метод не всегда подходит для поля в веществе. Так как равенство:

верно для вакуума, в веществе оно является приближенным. Сам процесс внесения пробного заряда в диэлектрик может оказаться невозможен, например, когда используемый диэлектрик — твердый.

Единственный способ измерения E → и D → , получивший название принципиального, заключается в том, чтобы создать внутри вещества полость и в нее внести пробный заряд.

Отметим при этом, что поле, измеренное подобным образом, не совпадет ни с вектором напряженности, ни с вектором индукции электрического поля. Итоговый результат будет зависеть от формы полости, в связи с чем в целях применения принципиального метода используют специальные формы полостей, в которых результат измерений E → и D → будет максимально близок к реальности.

Измерение векторов поля при помощи полостей

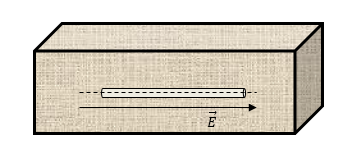
Возьмем для рассмотрения полость, имеющую форму длинного и тонкого цилиндрического канала. Этот канал является параллельным полю E → (рисунок 1 ). При этом будем считать, что в канале содержится вещество, количество которого бесконечно мало. Удалив вещество из диэлектрика, мы получим небольшое изменение электрического поля в среде. На концах канала появятся поляризационные заряды, влиянием которых на поле на достаточном удалении от концов полости можно пренебречь. На основе симметрии можно сказать, что поле в канале E 0 → параллельно внешнему полю E → . Из граничного условия следует, что:

В конечном счете мы приходим к тому, что измерение поля в диэлектрике есть измерение поля E 0 →

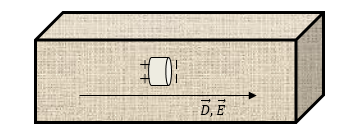
Рассмотрим другую форму плоскости: пусть это будет бесконечно короткий цилиндр, у которого основания являются перпендикулярными вектору индукции электрического поля D → (рисунок 2 ).

Удалив в этом случае из диэлектрика вещество, мы не получим существенного влияния на электрическое поле в диэлектрике в целом. На границах полости появятся поляризационные заряды, имеющие противоположные знаки. За пределами полости будет происходить почти полная компенсация полей зарядов друг другом. В пределах полости поля зарядов будут усиливать друг друга, что повлечет за собой значимое изменение поля внутри полости. В пределах полости
E 0 → перпендикулярно к ее основаниям (в силу симметрии). Так как полость содержит воздух или вакуум:

Применим граничное условие и можем сделать следующий вывод:

Измерение электрического смещения сводится к измерению напряженности поля в полости.

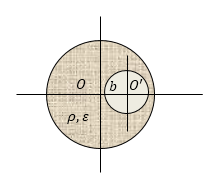
Пусть задан шар, имеющий равномерную заряженность (объемная плотность ρ ). Пусть в заданном шаре создана небольшая сферическая полость с центром O ‘ . Центр созданной полости расположен на расстоянии b от центра заданного диэлектрического шара О . Необходимо определить напряженность поля в центре полости.

Решение

Чтобы найти поле в полости, применим теорему Остроградского — Гаусса совместно с принципом суперпозиции. Определять поле будем в точке O ‘ , для чего создадим гипотетическую сферу, имеющую радиус b и центр в точке О . Запишем выражение для нахождения потока вектора электрического смещения сквозь поверхность данной сферы:

Φ D = ∮ S D d S = q , где q = 4 3 π b 3 ρ , S = 4 π b 2 . Для поля шара присуща сферическая симметрия, тогда из выражения Φ D = ∮ S D d S = q запишем:

D S = D 4 π b 2 = 4 3 πb 3 ρ → D = bρ 3 .

Поляризационные заряды в полости создадут поле D ‘ → ; согласно принципу суперпозиции итоговое поле в точке O ‘ определяется как:

Полость не имеет свободных зарядов, тогда, согласно теореме Остроградского-Гаусса:

Граничные условия определяют тот факт, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков неизменна. Таким образом:

Резюмируя все наши рассуждения, сделаем запись выражения для поля внутри полости:

D O ‘ → = D = b ρ 3 .

Напряженность поля в полости определится как:

Ответ: поле в полости D O ‘ → = b ρ 3 , E → = b → ρ 3 , где b → является вектором, соединяющим точки O и O ‘ .

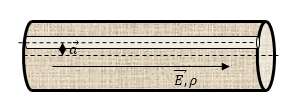
Задана бесконечно длинная цилиндрическая полость, расположенная в бесконечно длинном цилиндре, который равномерно заряжен по объему ( ρ – плотность заряда) и имеет радиус R . Оси цилиндра и полости параллельны и удалены на некоторое расстояние друг от друга. Необходимо определить напряженность электрического поля на оси полости.

Решение

Чтобы определить поле в полости, применим теорему Остроградского – Гаусса совместно с принципом суперпозиции. Чтобы найти поле цилиндра на прямой, где должна находиться ось полости, создадим гипотетическую цилиндрическую поверхность радиуса a с осью, совпадающей с осью основного цилиндра. Запишем выражение для потока вектора электрического смещения сквозь поверхность заданного цилиндра:

Φ E = ∮ S D d S = q , где q = π a 2 h ρ , S = 2 π a h ( h является высотой цилиндра).

Для поля шара присуща цилиндрическая симметрия, тогда из выражения Φ D = ∮ S D d S = q запишем:

D S = D 2 π a h = π a 2 h ρ → D = a ρ 2 .

Поляризационные заряды в полости создадут поле D ‘ → ; согласно принципу суперпозиции итоговое поле на оси полости определяется как:

Полость не имеет свободных зарядов, тогда, согласно теореме Остроградского-Гаусса:

Граничные условия определяют тот факт, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков неизменна. Таким образом:

Резюмируя все наши рассуждения, сделаем запись выражения для поля внутри полости:

Напряженность поля в полости определится как:

Ответ: E → = a → ρ 2 ε 0 .

Источник

Современные методы измерения напряженности электрического поля

СОВРЕМЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Омский государственный технический университет, г. Омск, Россия

Аннотация. В данной статье представлена проблема измерения напряженности электрического поля промышленной частоты. Описаны главные трудности таких измерений и современные методы их решения. Отображены основные конструктивные решения и определены основополагающие тенденции дальнейшего развития данной области. Целью данного исследования является выявление наиболее точных и простых способов реализации прибора для измерения заданной физической величины. В ходе данной работы были установлены ведущие направления развития инженерной мысли в данной сфере.

Ключевые слова: напряженность, электрическое поле, измерение, оптические измерения, оптический датчик, конструкция датчика

В современном обществе существует потребность измерять различные параметры электромагнитных полей. Данное исследование посвящено описанию методов измерения напряженности электрической составляющей поля. Электромагнитное поле оказывает значительное влияние на различные электронные приборы. При определенном уровне напряженности существует вероятность искажения сигналов, возникновения наводок и пробоев. Кроме того, электрическое поле оказывает отрицательное влияние на организм человека. Все чаще в обществе стала подниматься проблема электромагнитного загрязнения окружающей среды. Поэтому существует необходимость знать уровень напряженности вблизи точных электрических приборов, а также вблизи мест постоянного проживания людей. Данная работа посвящена средствам и методам измерения электрических полей промышленной частоты, в России это частота порядка 50 Гц. Сложность таких измерений сводиться к тому, что необходимо иметь строго однозначную зависимость напряженности поля от информативного параметра, а также необходимо избежать внесения значительных искажений в существующее поле. Этими факторами определяется точность измерения. В статье будут представлены современные методы измерения напряженности и конкретные конструкции датчиков и приборов, основанные на оптическом методе, представленные в течение последних 10 лет исследований в данной области.

В настоящее время существуют различные методы измерения напряженности электрического поля. В ходе исследований были найдены следующие методы [6]: электроиндукционный метод, электропространственный метод, электромеханический метод, газоразрядный метод, емкостной метод, оптический метод.

В данной работе для более детального рассмотрения был выбран оптический метод. Данный метод прост в конструировании средств измерений, позволяет сделать портативное устройство для измерения напряженности вдали от источников питания, имеет широкий спектр эффектов, пригодных для данной цели, в наименьшей степени искажает исследуемое поле, что приводит к улучшению точности в сравнении с другими методами.

Для построения датчика электрического поля необходимо иметь объект, параметры которого будут меняться под действием этого поля. В качестве такого объекта чаще всего используются электрооптические кристаллы. В данных структурах можно наблюдать следующие физические эффекты:

· Эффект Поккельса (линейный электрооптический эффект) [6];

· Эффект Керра (квадратичный электрооптический эффект) [6];

Эффект Поккельса заключается в изменении показателя преломления света в кристаллах под действием электрического поля. Изменение данного показателя происходит пропорционально напряженности поля, вследствие чего происходит двойное лучепреломление, при этом изменяется и скорость движения волны. Объясняется это тем, что под действием электрического поля меняется поляризуемость кристалла, а как следствие и показатель преломления. Данный эффект достаточно широко используется в данной области, многие современные приборы для измерения напряженности электрического поля построены именно на нем.

Эффект Керра схож с эффектом Поккельса. Различие заключается лишь в среде, в которой наблюдается данное явление. Эффект Керра наиболее выражен в кристаллах имеющих центр симметрии или изотропных средах. Преломление, в отличие от линейного электрооптического эффекта, пропорционально квадрату напряженности поля, откуда и следует второе название – квадратичный электрооптический эффект.

Рассмотрим подробнее современные приборы и датчики для измерения напряженности электрического поля.

Первый вид датчиков, основанный на эффекте Поккельса, представлен следующим механизмом (Рис.1). Луч от лазерного светодиода поступает на поляризатор, плоско поляризованный луч проходит через ячейку Поккельса, попадает на анализатор, а затем на фотодиод. На фотодиоде оптический сигнал преобразуется в электрический, усиливается и подается на микроконтроллер для обработки и преобразования его в величину напряженности поля.

Рис.1. Измерительная цепь 1

Уравнение преобразования выглядит следующим образом:

где Δφ – фазовый сдвиг;

S – значение напряженности электрического поля;

k — коэффициент чувствительности изменения фазы;

l – длина чувствительного элемента.

Для увеличения точности вводят источник света, который облучает кристалл вдоль трех ортогональных друг другу направлений, показания снимаются также с трех направлений [3]. Это позволяет сделать прибор, показания которого не будут зависеть от его ориентации в пространстве, что приведет к уменьшению погрешности. Существует множество конструкций такого типа, имеющие небольшие различия в своем строении, однако схожие в их принципе работы [1, 2].

Зависимость скорости распространения поляризованного луча в электрооптическом кристалле от напряженности приложенного к нему поля так же используется для подобного рода измерений. Можно привести в качестве примера следующую измерительную цепь (Рис.2). Имеется источник оптического излучения, свет от которого через оптическое волокно попадает на коллиматорную линзу. Линза формирует два параллельных друг другу пучка. Оба пучка проходят через поляризатор, приобретая линейную поляризацию, которая далее преобразуется в круговую. После лучи проходят через кристалл и поляризационный оптический разветвитель. В кристалле под действием внешнего приложенного электрического поля появляется сдвиг фазы. Далее уже две волны с различными поляризациями и сдвинутые по фазе относительно первоначального сигнала подаются на фотоприемники и на блок обработки, где и определяется напряженность поля. В данном устройстве измерительный датчик и блок обработки с источником оптического излучения пространственно разделены. Связь осуществляется при помощи оптического волокна [5].

Рис.2. Измерительная цепь 2

Передаточная функция для данного устройства может быть представлена следующим образом:

,

где Eg – показатель чувствительности;

E – напряженность электрического поля;

α – показатель качества чувствительного элемента;

Δφ0 – первичный фазовый сдвиг в датчике.

Существует еще одно средство измерений (Рис.3). Данная модель рассчитана на более высокие частоты, но также относится к электрооптическим измерительным приборам для определения уровня напряженности. Возможности этого устройства гораздо шире, чем у других приборов данного класса. С помощью этого средства измерений возможно определить амплитуду, фазу, поляризацию, а также угол падения электромагнитной волны на приемную поверхность (датчик). На противоположных концах световода расположены источник и приемник световой волны, в центре находится чувствительный элемент, в котором в результате эффекта Керра происходит модуляция световой волны. Электромагнитная волна попадает на кристалл через Люнебергскую линзу, которая фокусирует волну на чувствительном элементе. Таким образом, мы можем судить о характеристиках электрического поля [4].

Рис.3. Измерительная цепь 3.

Регистрируемая разность фаз находится следующим образом:

,

где – сдвиг фаз;

a – фазовый сдвиг фазовращателя;

b – амплитуда составляющей вектора электрического поля.

Стоит отметить, что для измерения напряженности полей высоких частот существует гораздо более широкий спектр приборов, среди которых оптические средства измерения занимают не такую объемную долю, как для измерения полей промышленной частоты.

Подводя итог данной работы можно прийти к заключению, что оптический метод широко используется в современных приборах. В основном, обладатели патентов отдают предпочтение эффекту Поккельса, хотя и регистрируют его разными способами. Также стараются пространственно разделять чувствительный элемент и блок обработки сигналов. Общая тенденция направлена на использование лазерных источников и оптоволокна, что уменьшает искажение исследуемого поля прибором и увеличивает точность измерений.

1. Пат. 2539130 Российская Федерация, МПК G 01 R 29/12. Волоконно-оптическое устройство для измерения напряженности электрического поля / , , № 000/28; заявл. 31.07.13, опубл. 10.01.15, Бюл.№1.

2. Пат. JP2014215140A Япония. Electric field measuring apparatus // Yoshikazu Toba, Atsushi Ichijo; заявл. 25.04.13, опубл. 17.11.14.

3. Пат. JP2006145244A Япония. Electric field measuring apparatus // Nakamatsu Shin, Onishi Teruo, Kamibayashi Shinji; заявл. 25.05.06, опубл. 06.12.07.

4. Пат. US5384458A США. Photonic electromagnetic field sensor for use in a missile // Donald P. Hilliard, Dean L. Mensa; заявл. 01.07.93, опубл. 24.01.95.

5. , Закурдаева построения и конструирования электрооптических систем // Электротехнические и информационные комплексы и системы. 2015. Т.11, №4. С. 115 – 124.

6. Бирюков основы измерения параметров электрических полей: моногр. — Омск: Изд-во СибАДИ, 2008. -112 с.

Источник