Способы измерения больших расстояний

Основные способы измерения расстояний на местности и по карте.

При выполнении различных задач в разведке, при наблюдении за полем боя, при целеуказании и ориентировании на местности, при подготовке данных для стрельбы и т.д. возникает необходимость быстро определять расстояние до ориентиров, местных предметов, целей в других объектов.

Существуют различные способы и приборы для определения расстояний на местности: по карте, аэрофотоснимку, с помощью дальномера и т.д. Но существуют и более простые способы измерения, такие как:

— определение расстояний на глаз;

— по угловым и линейным размерам предметов;

— по времени движения;

— по соотношению скоростей света и звука;

а) Глазомер. Это способ является наиболее распространенным и доступен каждому, так как расстояния определяются без применения каких — либо приборов, что очень важно в условиях боевой обстановки. Основные приёмы глазомерного определения — по отрезкам местности, по степени видимости предмета (цели).

По отрезкам местности. Этот приём заключается в способности наблюдателя мысленно представлять на местности привычные расстояния, например 100, 200, 300, 400м, Запечатлев эти отрезки в своей памяти, наблюдатель мысленно откладывает нужный отрезок в глубину столько раз, сколько он уложится до наблюдаемого предмета.

По степени видимости предмета. Определяя расстояние этим приёмом, нужно учитывать, на каком фоне местности находится предмет (цель) и вблизи каких других предметов он расположен.Определяя расстояние по степени видимости предметов, необходимо также учитывать что:

— мелкие предметы (кусты, бугры, камни), а также отдельные фигуры людей кажутся дальше, чем находящихся на том же расстоянии крупные предметы (лес, высота, населённый пункт, колонна);

— одноцветный, однообразный фон местности (луг, снег, пашня) как бы приближает находящиеся на нем предметы; разноцветный фон, наоборот, маскирует и как бы удаляет их;

— предметы легких цветов лучше видны, чем предметы тёмного цвета;

— при наблюдении ночью предметы, освещённые искусственным светом, кажутся ближе, а не освещённые — дальше, чем в действительности.

Практикой установлено, что погрешность точности глазомерного определения расстояний до 1000 м при наличии некоторого опыта может быть в пределах 10- 15 % длины измеряемого отрезка. При измерении расстояний более 1000м и недостаточной опытности, наблюдается ошибка, она может достигать 30 и даже 50%.

Для определения расстояний по степени видимости и кажущейся величины предметов (целей) рекомендуется воспользоваться таблицей 1 (см. приложение №1).

Определение расстояний по линейным размерам предметов даёт более точные результаты, чем глазомер, но для этого нужно знать действительные размеры наблюдаемого предмета и иметь линейку с миллиметровыми делениями.

Сущность этого способа состоит в том, что держа линейку на расстоянии наблюдаемого предмета.

Затем действительную высоту (ширину) предмета в см делят на измеренную по линейки высоту (ширину) предметов мм и умножают на постоянное число 5, Полученный результат и будет искомым расстоянием в метрах.

Например. Телеграфный столб высотой 6,4м закрывается 10 мм на линейке, Следовательно, до него:

Средние размеры наиболее часто встречающихся предметов приводятся в таблице 2 (см. приложение №2).

б) Определение расстояний по угловым размерам предметов основано на зависимости между угловыми и линейными величинами. Эта зависимость состоит в том, что длина 1/6000 любой окружности равна 1/1000 её радиуса.

Угол при центре окружности, соответствующей 1/6000 её дуги, принимается за единицу при условных измерениях вместо градусной меры. Эта единица называется тысячной. Тысячные читаются и записываются так: одна тысячная пишется “0-01”, читается “ноль ноль один”; двадцать пять тысячных — “0-25” — “ноль двадцать пять”; сто двадцать пять тысячных — “1-25”- “один двадцать пять”.

Высота предмета, выраженная в тысячных, может быть измерена биноклем с угломерной сеткой, линейкой с миллиметровыми делениями, а также с помощью подручных предметов, примеры которых в тысячных известны. Расстояние до предмета вычисляется по формуле:

где: В — высота (ширина) предмета, м;У — угловая величина предмета в тысячных.

Например, наблюдаемая в бинокль цель, высота которой равна 2,5м, покрывается делением сетки бинокля, равным 0-0,5. Следственно расстояние до цели:

S = 5 ” 1000 = 500 м

Измерение углов с миллиметровыми делениями производится также измерением высоты (ширины) цели, удерживая линейку на расстоянии 50см от глаз, при этой каждая миллиметровое деление будет соответствовать двум тысячным (0-0,8), а каждый сантиметр — двадцати тысячным (0-20).

Точность определения расстояний по линейному и угловыми величинам составляет 5-10% длины измеренного отрезка.

в) Измерение расстояния шагамипо сравнению с другими способами применяются ограниченно, только в тех случаях, когда позволяет обстановка.

При измерении расстояний шаги считаются парами. Чтоб измеренное расстояние перевести в метры, надо знать длину шага. Она определяется из промера шагами линии, длина известна или точно измерена заранее. Если пройденное расстояние достаточно определить приближённо, то принимают, что расстояние в метрах равно числу пар шагов, увеличенному в полтора раза, так как пара шагов в среднем равна 1_т5м.

Скорость своего движения и имея часы, легко подсчитать пройденное расстояние. Этот способ особенно полезен при движении на лыжах. Ошибка в измерениях расстояний шагами обычно составляет 2-4% от длины измеренного расстояния.

Определение расстояний по соотношению скорости света и звука. Скорость звука приблизительно равно 330м/сек, т.е. округлено 1км в 3сек. Скорость света равна 300000 км/сек, можно считать мгновенной. Таким образом расстояние в километрах до места вспышки равна числу секунд, прошедших от момента вспышки до того момента, когда наблюдатель услышал звук выстрела, деленному на три.

Определение расстояний на звук. Ночью и в условиях плохой видимости приблизительно расстояние до объектов, от которых издается звук или шум, можно оценить на слух. При нормальном случае и благоприятных условиях примерная дальность слышимости показана в таблице 1

Род войск или вид техники	Характер звука	Дальность слышимости, м
При движении по грунтовой дороге	При движении по шоссе
Подразделения в пешем строю Автомобили Артиллерия Танки	Ровный глухой шум шагов Ровный, глухой шум моторов Шум моторов, тягачей, лязг гусениц Резкий рокот моторов, лязг гусениц	1000-2000	2000-3000 3000-4000

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Способы измерения больших расстояний

Некоторое представление о глазомерной оценке расстояний может дать следующая таблица , в которой приведены предельные расстояния видимости объектов в дневное время для человека с нормальным зрением.

Наблюдаемый объект	Расстояние, км
Большие башни, маяки, элеваторы	16-20
Населенные пункты (общим контуром)	10-12
Фабричные корпуса и трубы	6
Небольшие отдельно стоящие дома, избы	4
Трубы на крышах	2-3
Отдельные высокие деревья	2-3
Стволы деревьев, телеграфные столбы, километровые столбы, фигура человека (общий контур)	1
Движения рук и ног идущего человека	0,6-0,7
Сучья и ветви на деревьях	0,4-0,6
Овал лица, цвет и части одежды человека, переплеты рам в окнах	0,3
Черепица на крыше, листья деревьев, проволока на кольях	0,2
Черты лица, глаза, кисти рук человека	0,07-0,1

Для развития глазомера необходимо иметь представление о том, как далеко лежит от наблюдателя линия горизонта. Дальность горизонта (ДГ) определяется по формуле:

Человек ростом 170 см, стоя на ровной местности, видит линию горизонта на расстоянии около 4,5 км, а поднявшись на высоту 5 м, может наблюдать местность в радиусе до 9 км.

Определение расстояний по времени и скорости движения .
В качестве вспомогательного способа для общего ориентирования можно применить расчет пройденного расстояния, зная время движения и среднюю скорость. Время движения можно определить довольно точно по часам или секундомеру. Сложнее обстоит дело с определением в походных условиях средней скорости движения группы. Причем трудности возникают как с определением абсолютной величины скорости, так и с поддержанием ее постоянства. Однако в некоторых видах путешествии (сплав по реке, движение на лыжах) все-таки возникает необходимость в определении скорости. В каждом конкретном случае надо пытаться определить скорость движения, например по известному отрезку пути, и затем, двигаясь в том же темпе, можно использовать ранее определенное значение скорости и время для расчета неизвестного отрезка пути. Более подробно о скорости движения группы будет рассказано дальше.
В авто-, мото-, а также велосипедном путешествиях пройденный путь определяет спидометр или специальный счетчик, установленный на велосипеде. Интересно, что тот же принцип определения пройденного пути можно использовать в лыжном и пешем походах. Полярные исследователи издавна пользуются для этой цели одометром — прибором, состоящим из колеса, например от детского велосипеда, с насечкой на ободе и счетчика оборотов. Колесо прикрепляется специальным кронштейном к нартам или саням. Для повышения точности измерения одометр прокатывают несколько раз по заранее отмеренному отрезку для определения поправки на проскальзывание по льду или снежному насту. Для простоты расчетов составляют таблицу пройденного расстояния.

Определение расстояний по линейным размерам предметов.

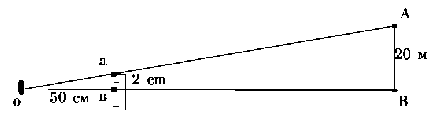
Определение расстояний по известным линейным размерам предметов, расположенных на местности. Сущность этого способа видна из рисунке. Наблюдатель держит линейку, например, плиты спортивного компаса перед собой перпендикулярно лучу зрения на расстоянии 50 см от глаз и определяет по ней величины отрезка ав, закрывающего наблюдаемый объект (дерево высотой 20 м). Из подобия треугольников Оав и ОАВ видно, что:

ОА=АВ х Оа/ав=500м.

Для точного выдерживания базы измерения — в нашем примере 50 см — удобно пользоваться следующим приемом. Длина вытянутой руки фиксируется бичевкои или ниткой с двумя узлами, удаленными друг от друга на заранее точно вымеренный отрезок (50 см). Один узелок зажимается зубами, а другой прижимается пальцем к линейке.
Карты. Основные понятия
Определение направлений и сторон горизонта

Источник

Способы измерения больших и малых расстояний

Большие расстояния

Как далеко от нас предметы? Как велики они? Надо взять какую-нибудь единицу длины и измерить, сколько таких единиц укладывается на данном отрезке. А как измерить предметы, которые меньше данной единицы длины? Надо взять меньшую единицу и измерить, сколько меньших единиц укладывается на большей, которая известна и т.д.

А как измерить расстояние до удаленных объектов, например, в космосе? Можно использовать метод триангуляции, который ясен из рисунков.

Расстояние до Венеры было измерено методом прямой радиолокационной связи. Здесь изменено определение понятия «расстояние». Мы считаем, что скорость радиоволны постоянна и известна (скорость света). Измеряем время прихода отраженной волны и вычисляем расстояние, как произведение скорости на время.

А как определять очень большие расстояния до звезд? Астрономы научились делать это по цвету свечения звезды. Обнаружена гладкая зависимость между цветом свечения и истинной яркостью звезд. Если теперь измерить цвет отдаленной звезды, то по этой зависимости можно определить расстояние (для данной истинной яркости видимая яркость уменьшается как квадрат расстояния). Таким образом определено расстояние до центра нашей Галактики, которое составляет около 10 20 м. Данные о размерах нашей Галактики дают ключ к определению еще больших межгалактических расстояний. Имеются веские соображения, по которым размеры всех Галактик приблизительно одинаковы. Зная угол, под которым смотрятся противолежащие границы другой Галактики и, предполагая, что размер ее равен размеру нашей, который известен, определяем расстояние до этой Галактики. Например, самое далекое измеренное расстояние до дальней Галактики составляет 10 26 м. Полагают, что это половина размера нашей Вселенной.

Малые расстояния

С помощью оптического микроскопа принципиально невозможно увидеть предметы меньшие, чем длина волны видимого света (5×10 -7 м). С помощью электронного микроскопа можно увидеть и измерить объекты вплоть до 10 -8 м. В электронном микроскопе изображение объекта создается с помощью электронного пучка, который отражается или проходит сквозь объект, преобразуется с помощью электронной оптики и попадает на люминесцентный экран, где можно наблюдать глазом сильно увеличенное электронной оптикой изображение объекта.

С помощью косвенных измерений (своего рода триангуляции в микроскопическом масштабе) можно измерить еще более мелкие объекты. Сначала из наблюдений отражения рентгеновских лучей от образца с нанесенными на известном расстоянии метками определяется длина волны излучения. Затем по картине рассеяния того же излучения на кристалле можно определить относительное расположение в нем атомов. Таким образом определяется и диаметр атомов » 10 -10 м.

Далее на шкале расстояний имеется довольно большая незаполненная щель между атомными (10 -10 м) и ядерными размерами (10 -15 м).

Эффективные сечения s ядер атомов можно определить, пропуская пучок частиц высокой энергии через тонкую пластинку вещества и измеряя число частиц, не прошедших сквозь нее. Эти высокоэнергетические частицы прорываются сквозь облачко электронов, но задерживаются или отклоняются ядрами. Предположим, что имеется пластинка известной толщины, на которой укладывается известное число атомных слоев. Ядра настолько малы, что можно пренебречь вероятностью того, что одно ядро заслонит другое от пучка частиц. Вероятность того, что малая частица столкнется с ядром, равно отношению площади sN (N — число атомов пластины, попадающих в поперечное сечение пучка), занимаемой ядрами, к площади S поперечного сечения пучка. Пусть число частиц, попадающих на пластину равно n₁, а вышедших из нее — n₂. Тогда:

, где r — радиус ядра.

Таким образом определены размеры ядер 1-6×10 -15 м. Единица длины 10 -15 м названа ферми в честь итальянского физика Энрико Ферми (1901-1958гг.).

Стандарты длины

Ранее стандартом длины был 1 м = (p/2)×10 -7 доли Земного радиуса.

Затем эталоном метра стал брусок из благородного металла с двумя нанесенными на нем метками.

Сейчас действует стандарт длины, как некоторое заранее обусловленное число длин волн определенной спектральной линии.

Результаты измерения расстояний и времени зависят от наблюдателя. Два наблюдателя, движущиеся друг относительно друга, измеряя один и тот же предмет или длительность одного и того же процесса получат разные значения, хотя, казалось бы, измеряли одно и то же. Это объясняется теорией относительности.

Законы природы не позволяют выполнять абсолютно точно измерения расстояний или интервалов времени. Ошибка в определении положения частицы не может быть меньше, чем Dх = h/Dр, где h — малая величина (постоянная Планка), Dр — ошибка в определении импульса частицы (р = mv). Эта неопределенность связана с волновой природой вещества.

Измерение интервалов времени также не может быть точнее, чем Dt = h/DE, где DE — ошибка в определении энергии того процесса, длительность которого определяется. Иными словами, чтобы знать более точно, когда что-то произошло, мы вынуждены довольствоваться тем, что знаем менее точно, что же именно произошло, поскольку наши знания об энергии, участвующей в процессе будут менее точными. Это тоже связано с волновой природой вещества.

Векторы

Физические законы обладают двумя свойствами, которые называют инвариантностью (или симметрией) относительно перемещений и поворотов координатных осей. Эти свойства так важны, что для учета их при изучении физических законов была разработана специальная математическая техника, называемая векторным анализом.

Важно различать физические величины двух типов. Величины первого типа характеризуются только численным значением (например, температура, количество предметов и т.д.) — это скаляры. Другие величины — векторы — характеризуются не только численным значением, но и направлением в пространстве. Численные значения физических величин и их направление в каждой точке пространства не зависят от выбора системы координат. Например, перемещение из начала координат в точку Р(х,у,z) (шаг в пространстве, который имеет определенную длину и направление).

Вектор определяется тремя числами — его проекциями на координатные оси. Например, перемещение из начала координат в точку Р(х,у,z) можно описать тремя числами х,у,z. Но можно использовать для этой цели один — единственный символ r (радиус-вектор). Символ r задается не только тремя числами х,у,z, но и числами в другой системе координат. Т.е. мы используем один и тот же символ в качестве представителя трех чисел в одной системе координат и делаем его представителем второго набора чисел, если захотим сменить систему координат. Это удобно потому, что не придется изменять форму уравнений при изменении системы координат. Очевидно, что проекции вектора при изменении системы координат должны измениться по строго определенным законам, таким же, как и тройки чисел х,у,z и . Только в этом случае, проекции вектора отображают один и тот же объект во всех системах координат. Для шага в пространстве нам очевидно, что это один и тот же объект во всех системах координат (шаг имеет определенную длину и направление в пространстве не зависящие от выбора системы координат). А бывают случаи, когда требуется специальное исследование, устанавливающее, по каким законам изменяются тройки чисел, характеризующие величину, при изменении системы координат, заранее это не очевидно. Если эти законы такие же, как и для тройки чисел х,у,z, то величине присваивается статус вектора (объекта, не зависящего от выбора системы координат).

Определим вектор математически как величину, определяемую тремя числами, которые преобразуются при изменении системы координат так же, как и координаты. То, что физические соотношения между какими-то величинами можно выразить в форме векторных уравнений отражает тот факт, что эти соотношения верны в любой системе координат.

Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление. Стрелка преобразуется при изменении системы координат по тем же законам, что и шаг в пространстве. Изобразив ее, не нужно заботиться о координатных осях.

Внимание!

Вектор обозначается жирным шрифтом (например, r, v, a). В рукописях (конспекте и т.п.)вектор обозначается стрелкой, или черточкой над буквой.

Полезно увидеть законы преобразования хотя бы в упрощенном частном случае. Например, одна система координат повернута относительно другой вокруг оси z на угол q. Начало координат в обеих системах совпадает.

(1)

Источник