Регулирование скорости двигателей постоянного тока
Из уравнения электромеханической характеристики двигателя постоянного тока независимого возбуждения следует, что возможны три способа регулирования его угловой скорости:
1) регулирование за счет изменения величины сопротивления реостата в цепи якоря,
2) регулирование за счет изменения потока возбуждения двигателя Ф,
3) регулирование за счет изменения подводимого к обмотке якоря двигателя напряжения U . Ток в цепи якоря I я и момент М, развиваемый двигателем, зависят только от величины нагрузки на его валу.
Рассмотрим первый способ регулирования скорости двигателя постоянного тока изменением сопротивления в цепи якоря . Схема включения двигателя для этого случая представлена на рис. 1 , а электромеханические и механические характеристики — на рис. 2 , а.
Рис. 1. Схема включения двигателя постоянного тока независимого возбуждения
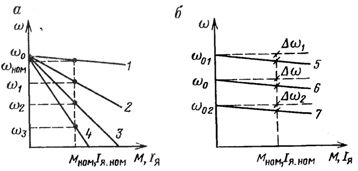
Рис. 2. Механические характеристики двигателя постоянного тока при различных сопротивлениях цепи якоря (а) и напряжениях (б)
Изменяя сопротивление реостата в цепи якоря можно получить при номинальной нагрузке различные угловые скорости электродвигателя на искусственных характеристиках — ω1, ω2, ω3.
Проведем анализ данного способа регулирования угловой скорости двигателей постоянного тока с помощью основных технико-экономических показателей. Так как при данном способе регулирования изменяется жесткость характеристик в широких пределах, то при скоростях менее половины номинальной стабильность работы двигателя резко ухудшается. По этой причине диапазон регулирования скорости ограничен ( D = 2 — З).
Скорость при данном способе можно регулировать в сторону уменьшения от основной, о чем свидетельствуют электромеханические и механические характеристики. Высокую плавность регулирования трудно обеспечить, так как потребовалось бы значительное количество ступеней регулирования и соответственно большое число контакторов. Полное использование двигателя по току (нагреву) в этом случае достигается при регулировании с постоянным моментом нагрузки.
Недостатком рассматриваемого способа является наличие значительных потерь мощности при регулировании, которые пропорциональны относительному изменению угловой скорости. Достоинством рассмотренного способа регулирования угловой скорости являются простота и надежность схемы управления.
Учитывая большие потери в реостате при малых скоростях, данный способ регулирования скорости применяется для приводов с кратковременным и повторно-кратковременным режимами работы.
При втором способе регулирование угловой скорости двигателей постоянного тока независимого возбуждения осуществляется изменением величины магнитного потока за счет введения в цепь обмотки возбуждения дополнительного реостата. При ослаблении потока угловая скорость двигателя как при нагрузке, так и при холостом ходе возрастает, а при усилении потока — уменьшается. Практически возможно изменение скорости только в сторону увеличения ввиду насыщения двигателя.
При увеличении скорости ослаблением потока допустимый момент двигателя постоянного тока изменяется по закону гиперболы, а мощность остается постоянной. Диапазон регулирования скорости для данного способа D = 2 — 4 .
Механические характеристики для различных значений потока двигателя приведены на рис. 2 , а и 2 , б, из которых видно, что характеристики в пределах номинального тока имеют высокую степень жесткости.
Обмотки возбуждения двигателей постоянного тока независимого возбуждения обладают значительной индуктивностью. Поэтому при ступенчатом изменении сопротивления реостата в цепи обмотки возбуждения ток, а следовательно, и поток будут изменяться по экспоненциальному закону. В связи с этим регулирование угловой скорости будет осуществляться плавно.
Существенными преимуществами данного способа регулирования скорости являются его простота и высокая экономичность.
Данный способ регулирования используют в приводах в качестве вспомогательного, обеспечивающего повышение скорости при холостом ходе механизма.
Третий способ регулирования скорости заключается в изменении напряжения, подводимого к обмотке якоря двигателя. Угловая скорость двигателя постоянного тока независимо от нагрузки изменяется прямо пропорционально напряжению, подводимому к якорю. Поскольку все регулировочные характеристики являются жесткими, а степень их жесткости остается для всех характеристик неизменной, работа двигателя является стабильной на всех угловых скоростях и, следовательно, обеспечивается широкий диапазон регулирования скорости независимо от нагрузки. Этот диапазон равен 10 и может быть расширен за счет специальных схем управления.
При данном способе угловую скорость можно уменьшать и увеличивать относительно основной. Повышение скорости ограничено возможностями источника энергии с регулируемым напряжением и U ном двигателя.
Если источник энергии обеспечивает возможность непрерывного изменения подводимого к двигателю напряжения, то регулирование скорости двигателя будет плавным.
Данный способ регулирования является экономичным, так-так регулирование угловой скорости двигателя постоянного тока независимого возбуждения осуществляется без дополнительных потерь мощности в силовой цепи якоря. По всем перечисленным выше показателям данный способ регулирования по сравнению с первым и вторым наилучший.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Способы изменения величины скоростей
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) — наклонная линия :
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
— если известны начальная, конечная скорости движения и ускорение.
— если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:
В координатах зависимость имеет вид:
Источник
