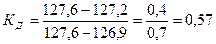Методы исключения грубых погрешностей



Грубая погрешность, или промах – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором.
К ним можно отнести:
• неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
• неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь;
• хаотические изменения параметров питающего СИ напряжения, например его амплитуды или частоты.
Корректная статистическая обработка выборки возможна только при ее однородности, т.е. в том случае, когда все ее члены принадлежат к одной и той же генеральной совокупности. В противном случае обработка данных бессмысленна. «Чужие» отсчеты по своим значениям могут существенно не отличаться от «своих» отсчетов. Их можно обнаружить только по виду гистограмм или дифференциальных законов распределения. Наличие таких аномальных отсчетов принято называть загрязнениями выборки , однако выделить члены выборки, принадлежащие каждой из генеральных совокупностей, практически невозможно.
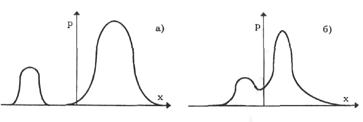
Если «свои» и «чужие» отсчеты различаются по значениям, то их исключают из выборки (рис.6.1,а). Особую неприятность доставляют отсчеты, которые хотя и не входят в компактную группу основной массы отсчетов выборки, но и не удалены от нее на значительное расстояние, – так называемые предполагаемые промахи (рис. 6.1,6).
Рисунок 6.1 – Проявление промахов на дифференциальном законе распределения вероятности
Отбрасывание «слишком» удаленных от центра выборки отсчетов называется цензурированием выборки. Это осуществляется с помощью специальных критериев.
При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений.
Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения хi не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.
Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.
Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q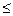
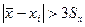
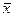
Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при 6 Данное правило также применимо только для нормального закона.
В общем случае границы цензурирования tгр, Sх выборки зависят не только от объема n, но и от вида распределения. Назначая ту или иную границу, необходимо оценить уровень значимости q, т.е. вероятность исключения какой-либо части отсчетов, принадлежащих обрабатываемой выборке.
Выражение для приближенного расчета коэффициента tгр при уровне значимости q 
• кругловершинных двухмодальных распределений с ε = 1,5, 3, являющихся композицией дискретного двузначного и нормального распределений;
• островершинных двухмодальных распределений с ε = 1,5, 6, являющихся композицией дискретного двузначного распределения и распределения Лапласа;
• композиций равномерного и экспоненциальных распределений с показателем степени α = 1/2 при ε = 1,8, 6;
• экспоненциальных распределений с ε = 1,5, 6.
Критерий Романовского применяется, если число измерений n βт, то результат xi считается промахом и отбрасывается.
Пример 6.3. При диагностировании топливной системы автомобиля результаты пяти измерений расхода топлива составили: 22, 24, 26, 28, 30 л на 100 км. Последний результат вызывает сомнение. Проверить по критерию Романовского, не является ли он промахом.
Значения критерия Романовского β = f(n)
| q | n = 4 | n = 6 | n = 8 | n = 10 | n = 12 | n = 15 | n = 20 |
| 0,01 0,02 0,05 0,10 | 1,73 1,72 1,71 1,69 | 2,16 2,13 2,10 2,00 | 2,43 2,37 2,27 2,17 | 2,62 2,54 2,41 2,29 | 22,75 2,66 2,52 2,39 | 2,90 2,80 2,64 2,49 | 3,08 2,96 2,78 2,62 |
Найдем среднее арифметическое значение расхода топлива и его СКО без учета последнего результата, т.е. для четырех измерения. Они соответственно равны 25 и 2,6 л на 100 км.
Критерий Романовского свидетельствует о необходимости отбрасывания последнего результата измерения.
Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд x1, х2, хn (х1 Zp) = q. Значения Zp приведены в табл. 6.2.
Пример 6.4. Было проведено пять измерений напряжения в электросети. Получены следующие данные: 127,1; 127,2; 126,9; 127,6; 127,2 В. Результат 127,6 В существенно (на первый взгляд) отличается от остальных. Проверить, не является ля он промахом.
Составим вариационный ряд из результатов измерений напряжения в электросети: 126,9; 127,1; 127,2; 127,2; 127,6 В. Для крайнего члена этого ряда (127,6 В) критерий Диксона
Значения критерия Диксона
| n | Zq при q, равном | ||
| 0,10 | 0,05 | 0,02 | 0,01 |
| 0,68 0,48 0,40 0,35 0,29 0,28 0,26 0,26 0,22 | 0,76 0,56 0,47 0,41 0,35 0,33 0,31 0,30 0,26 | 0,85 0,64 0,54 0,48 0,41 0,39 0,37 0,36 0,31 | 0,89 0,70 0,59 0,53 0,45 0,43 0,41 0,39 0,34 |
Как следует из табл.6.2, по этому критерию результат 127,6 В может быть отброшен как промах лишь на уровне значимости q = 0,10.
Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерений. Конечно, оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но он не имеет права отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем привлекать на помощь рассмотренные выше статистические критерии. Кроме рассмотренных критериев, существуют и другие, например критерии Граббса и Шовенэ.
Источник
Выявление и исключение грубых погрешностей (промахов)
Погрешности измерений
Истинным называется значение ФВ, идеальным образом характеризующее свойство данного объекта как в количественном, так и в качественном отношении. Действительным называется значение ФВ, найденное экспериментально и настолько близкое к истинному, что в поставленной измерительной задаче оно может быть использовано вместо него. Результат измерения представляет собой значение величины, полученное путем измерения.
Погрешность результата измерения – это отклонение результата измерения X от истинного (или действительного) значения Q измеряемой величины: DX = X —Q.
Погрешность средства измерений – разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность средства измерений (характеристику качества СИ, отражающую близость его погрешности к нулю).
По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и промахи, или грубые погрешности.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях.
Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Грубая погрешность (промах) – это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений; для данных условий она резко отличается от остальных результатов этого ряда.
По способу выражения различают абсолютную, относительную и приведенную погрешности.
Абсолютная погрешность описывается формулой и выражается в единицах измеряемой величины.
Относительная погрешность есть отношение абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины: δ=Δx/x.
Приведенная погрешность средства измерений – это относительная погрешность, в которой абсолютная погрешность СИ отнесена к условно принятому значению xN , постоянному во всем диапазоне измерений или
его части: γ=Δx/xN . Условно принятое значение xN называют нормирующим.
В зависимости от причин возникновения различают инструментальные погрешности измерения, погрешности метода измерений, погрешности из-за изменения условий измерения и субъективные погрешности измерения.
Инструментальная погрешность измерения обусловлена погрешностью применяемого СИ. Иногда эту погрешность называют аппаратурной.
Погрешность метода измерений – составляющая систематической погрешности измерений из-за несовершенства принятого метода измерений, эта погрешность обусловлена:- отличием принятой модели объекта измерения от модели, адекватно описывающей его свойство, которое определяется путем измерения;
— влиянием способов применения СИ, влиянием алгоритмов (формул), по которым производятся вычисления результатов измерений.
Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов.
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности: аддитивные Δa , не зависящие от измеряемой величины; мультипликативные Δм , которые прямо пропорциональны измеряемой величине, и нелинейные Δн , имеющие нелинейную зависимость от измеряемой величины.
В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на статические и динамические.
Статическойназывается погрешность средства измерений, применяемого для измеренияФВ, принимаемой за неизменную. Динамическойназывается погрешностьСИ, возникающая дополнительно при измерении изменяющейся (в процессе измерений) ФВ.
Выявление и исключение грубых погрешностей (промахов)
Грубая погрешность, или промах– это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Источником грубых погрешностей нередко бывают ошибки, допущенные оператором во время измерений.
К ним можно отнести:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь.
Отбрасывание «слишком» удаленных от центра выборки отсчетов называется цензурированиемвыборки.
Это осуществляется с помощью специальных критериев.При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений. Вопрос о том, содержит ли результат наблюдений грубую погрешность,решается общими методами проверки статистических гипотез .Проверяемая гипотеза состоит в утверждении, что результат наблюдения х, не содержит грубой погрешности, т.е. является одним из значений
измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую
погрешность и его исключают.Для выявления грубых погрешностей задаются вероятностью q —
уровнем значимости того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.
Критерий «трех сигм» применяется для результатов измерений,распределенных по нормальному закону. По этому критерию считается,что результат, возникающий с вероятностью q 3Sx , где Sx – оценка СКО измерений. Величины X и Sx вычисляют без учета экстремальных значений xi . Данный критерий надежен при числе измерений n ³20. 50.
Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при 6
Вариационный критерий Диксона – удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд
x1, x2 ,_, xn x1 Zq )= q . Значения Zq приведены в таблице.
Источник