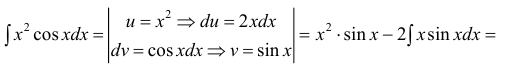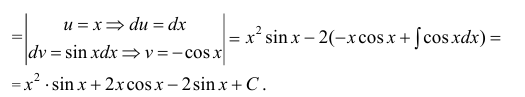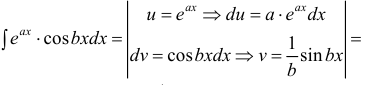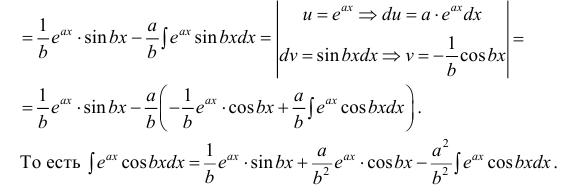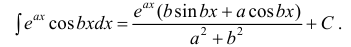- Методы вычисления неопределенных интегралов
- Первообразная и неопределенный интеграл
- Основные формулы и методы интегрирования
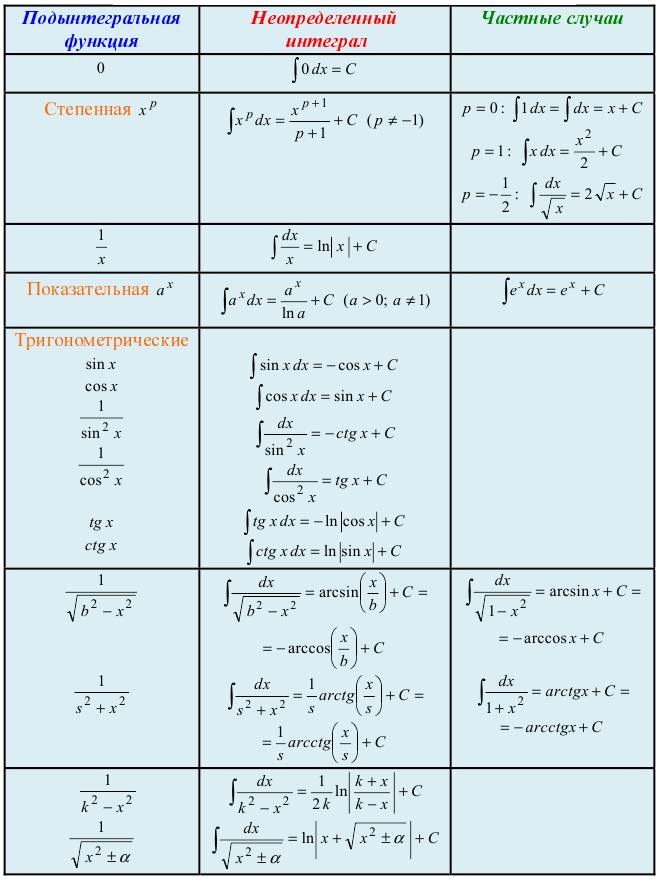
- Таблица интегралов
- Правило интегрирования суммы (разности)
- Вынесение постоянной за знак интеграла
- Замена переменной
- Правило интегрирования по частям
- Интегрирование дробей (рациональных функций)
- Интегрирование иррациональных функций
- Дробно-линейная иррациональность
- Интегралы от дифференциальных биномов
- Интегралы, содержащие квадратный корень из квадратного трехчлена
- Подстановки Эйлера
- Тригонометрические и гиперболические подстановки
- Прямые методы
- Интегрирование трансцендентных (тригонометрических и показательных) функций
- Интегрирование рациональных тригонометрических функций от cos x и sin x
- Произведение степенных функций от cos x и sin x
- Интегрирование по частям
- Применение формулы Эйлера
- Методы интегрирования неопределенного интеграла с примерами решения
- Определения
- Свойства неопределенного интеграла
- Таблица основных неопределенных интегралов
- Методы интегрирования
- Метод тождественных преобразований под интегральной функции
- Метод замены переменной интегрирования
- Метод интегрирования по частям
- Неопределенный интеграл
- Свойства неопределенного интеграла
- Таблица интегралов
- Замена переменной в неопределенном интеграле
- Интегрирование по частям в неопределенном интеграле
Методы вычисления неопределенных интегралов
Первообразная и неопределенный интеграл
Первообразная F(x) от функции f(x) – это такая функция, производная которой равна f(x) :
F′(x) = f(x), x ∈ Δ ,
где Δ – промежуток, на котором выполняется данное уравнение.
Совокупность всех первообразных называется неопределенным интегралом:
,
где C – постоянная, не зависящая от переменной x .
Основные формулы и методы интегрирования
Таблица интегралов
Конечная цель вычисления неопределенных интегралов — путем преобразований, привести заданный интеграл к выражению, содержащему простейшие или табличные интегралы.
См. Таблица интегралов >>>
Правило интегрирования суммы (разности)
.
Здесь и далее u, v, w – функции от переменной x .
Вынесение постоянной за знак интеграла
Пусть c – постоянная, не зависящая от x . Тогда ее можно вынести за знак интеграла:
Замена переменной
Пусть x – функция от переменной t , x = φ(t) , тогда
.
Или наоборот, t = φ(x) ,
.
С помощью замены переменной можно не только вычислить простые интегралы, но и упростить вычисление более сложных.
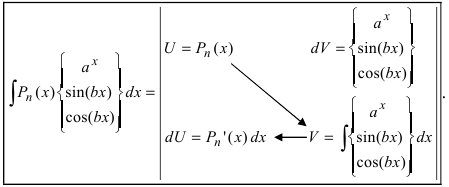
Правило интегрирования по частям
Интегрирование дробей (рациональных функций)
Введем обозначение. Пусть Pk(x), Qm(x), Rn(x) обозначают многочлены степеней k, m, n , соответственно, относительно переменной x .
Рассмотрим интеграл, состоящий из дроби многочленов (так называемая рациональная функция):
Если k ≥ n , то сначала нужно выделить целую часть дроби:
.
Интеграл от многочлена Sk-n(x) вычисляется по таблице интегралов.
Остается интеграл:
, где m .
Для его вычисления, подынтегральное выражение нужно разложить на простейшие дроби.
Для этого нужно найти корни уравнения:
Qn(x) = 0 .
Используя полученные корни, нужно представить знаменатель в виде произведения сомножителей:
Qn(x) = s (x-a) na (x-b) nb . (x 2 +ex+f) ne (x 2 +gx+k) ng . .
Здесь s – коэффициент при x n , x 2 + ex + f > 0 , x 2 + gx + k > 0 , . .
После этого разложить дробь на простейшие:
Интегрируя, получаем выражение, состоящее из более простых интегралов.
Интегралы вида
приводятся к табличным подстановкой t = x – a .
Рассмотрим интеграл:
Преобразуем числитель:
.
Подставляя в подынтегральное выражение, получаем выражение, в которое входят два интеграла:
,
.
Первый, подстановкой t = x 2 + ex + f приводится к табличному.
Второй, по формуле приведения:
приводится к интегралу
Приведем его знаменатель к сумме квадратов:
.
Тогда подстановкой , интеграл
также приводится к табличному.
Интегрирование иррациональных функций
Введем обозначение. Пусть R( u1, u2, . , un ) означает рациональную функцию от переменных u1, u2, . , un . То есть
,
где P, Q – многочлены от переменных u1, u2, . , un .
Дробно-линейная иррациональность
Рассмотрим интегралы вида:
,
где – рациональные числа, m1, n1, . ms, ns – целые числа.
Пусть n – общий знаменатель чисел r1, . rs .
Тогда интеграл сводится к интегралу от рациональных функций подстановкой:
.
Интегралы от дифференциальных биномов
Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.
1) Если p – целое. Подстановка x = t N , где N – общий знаменатель дробей m и n .
2) Если – целое. Подстановка a x n + b = t M , где M – знаменатель числа p .
3) Если – целое. Подстановка a + b x – n = t M , где M – знаменатель числа p .
Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.
В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям m и p . Это можно сделать с помощью формул приведения:
;
.
Интегралы, содержащие квадратный корень из квадратного трехчлена
Здесь мы рассматриваем интегралы вида:
,
Подстановки Эйлера
Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x1 – корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.
Тригонометрические и гиперболические подстановки
Также эти интегралы можно вычислить с помощью тригонометрических и гиперболических подстановок. В некоторых случаях этот способ вычисления интеграла является самым простым.
См. подробнее: Тригонометрические и гиперболические подстановки >>>
Прямые методы
В большинстве случаев, подстановки Эйлера приводят к более длинным вычислениям, чем прямые методы. С помощью прямых методов интеграл приводится к одному из перечисленных ниже видов.
I тип
Интеграл вида:
,
где Pn(x) – многочлен степени n .
Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:
Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты Ai .
II тип
Интеграл вида:
,
где Pm(x) – многочлен степени m .
Подстановкой t = ( x – α ) –1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.
III тип
Третий и наиболее сложный тип:
.
Здесь нужно сделать подстановку:
.
После чего интеграл примет вид:
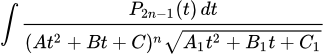
Далее, постоянные α, β нужно выбрать такими, чтобы коэффициенты при t обратились в нуль:
B = 0, B1 = 0 .
Тогда интеграл распадается на сумму интегралов двух видов:
;
,
которые интегрируются, соответственно подстановками:
z 2 = A1t 2 + C1 ;
y 2 = A1 + C1 t –2 .
Общий случай
Самый общий интеграл вида:
,
сводится к интегралам трех предыдущих типов. Для этого достаточно, уничтожая иррациональность в знаменателе, преобразовать подынтегральную функцию к виду:
φ(x) + ψ(x)y ,
где φ(x), ψ(x) – рациональные функции от x , . Далее,
,
где ω(x) – рациональная дробь. В последнем интеграле рациональную дробь ω(x) можно преобразовать выделением целой части и разложением на простейшие дроби. После этого получаются интегралы трех рассмотренных типов.
См. подробнее: Интегрирование рациональной функции от квадратного корня из квадратного трехчлена >>>
Интегрирование трансцендентных (тригонометрических и показательных) функций
Заранее отметим, что те методы, которые применимы для тригонометрических функций, также применимы и для гиперболических функций. По этой причине мы не будем рассматривать интегрирование гиперболических функций отдельно.
Интегрирование рациональных тригонометрических функций от cos x и sin x
Рассмотрим интегралы от тригонометрических функций вида:
,
где R – рациональная функция. Сюда также могут входить тангенсы и котангенсы, которые следует преобразовать через синусы и косинусы.
При интегрировании таких функций полезно иметь в виду три правила:
1) если R( cos x, sin x ) умножается на –1 от перемены знака перед одной из величин cos x или sin x , то полезно другую из них обозначить через t .
2) если R( cos x, sin x ) не меняется от перемены знака одновременно перед cos x и sin x , то полезно положить tg x = t или ctg x = t .
3) подстановка во всех случаях приводит к интегралу от рациональной дроби. К сожалению, эта подстановка приводит к более длинным вычислениям чем предыдущие, если они применимы.
Произведение степенных функций от cos x и sin x
Рассмотрим интегралы вида:
Если m и n – рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.
Если m и n – целые числа, то интегралы вычисляются интегрированием по частям. При этом получаются следующие формулы приведения:
Интегрирование по частям
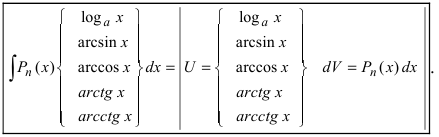
Интегралы, содержащие логарифм или обратные тригонометрические функции:
ln φ , arcsin φ , arctg φ , и т.д., где φ – некоторая алгебраическая функция от x , нередко интегрируются по частям, полагая u = ln φ , u = arcsin φ , u = arctg φ , и т.д.
Подробнее: Примеры решения интегралов по частям, содержащих логарифм и обратные тригонометрические функции >>>
Применение формулы Эйлера
Если подынтегральное выражение линейно относительно одной из функций
cos ax или sin ax , то удобно применить формулу Эйлера:
e iax = cos ax + i sin ax (где i 2 = – 1 ),
заменив эту функцию на e iax и выделив действительную (при замене cos ax ) или мнимую часть (при замене sin ax ) из полученного результата.
Таким способом удобно находить интегралы вида
, ,
где P(x) – многочлен от x .
См. подробнее: Интегрирование произведения многочлена, экспоненты и синуса или косинуса >>>
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 27-09-2014
Источник
Методы интегрирования неопределенного интеграла с примерами решения
Содержание:
При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.
Определения
Определение: Первообразной функции
Теорема: (о существовании первообразной) Если функция f(x) непрерывна на сегменте 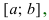
Теорема: Если F(x) — первообразная функции f(х), то функция F(x) + C (С -произвольная постоянная) также является первообразной функции f(х).
Доказательство:
ТЗ. Если 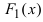
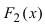
Доказательство: Пусть 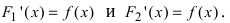
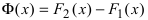
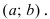
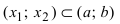
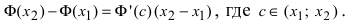
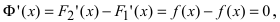
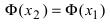
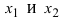
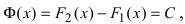
Пример:
Пусть дана функция 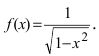
Решение:
В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
Для функции существуют две первообразные 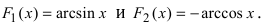
Определение: Совокупность всех первообразных функции 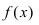
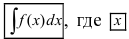
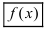
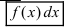
На основании теорем можно записать, что
Определение: Отыскание всех первообразных называется неопределенным интегрированием.
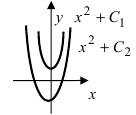
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 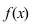
Пример:
Построить кривые, которые задаются неопределенным интегралом
Решение:
Первообразной для под интегральной функции f(х) = 2х будет функция 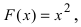
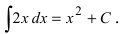
Рис. 1. Интегральные кривые
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна под интегральной функции
Доказательство: По определению неопределенного интеграла
2. Дифференциал неопределенного интеграла равен под интегральному выра- жению
Доказательство: По определению дифференциала от неопределенного интеграла имеем
3. Если под интегральное выражение является дифференциалом некоторой функции F(x), тo неопределенный интеграл равен
Доказательство: Так как
4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций
- а) неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций
- б) постоянный множитель можно выносить за знак неопределенного интеграла
5. Формула неопределенного интеграла не зависит от обозначения переменной интегрирования
Таблица основных неопределенных интегралов
Методы интегрирования
Метод тождественных преобразований под интегральной функции
Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.
1. Почленное деление числителя дроби на ее знаменатель
Замечание: Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.
Пример:
Найти
Решение:
Выполним в под интегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла
Замечание: Из этого примера видно, что слова «найти неопределенный интеграл” означают: за счет преобразований подынтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.
Замечание: Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования С пишется один раз, так как сумма или разность постоянных интегрирования все равно есть постоянная величина.
2. Использование противоположных арифметических операций (например, сложение-вычитание).
Пример:
Найти
Решение:
Анализ под интегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подынтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)
3. Использование алгебраических и тригонометрических формул, например,
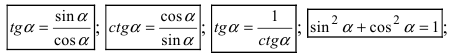
Пример:
Найти
Решение:
Воспользуемся формулой квадрата разности
Пример:
Найти
Решение:
4. Использование свойств функций, например,
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
5. Использование разложения полиномов на простые множители, например, 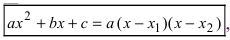
Пример:
Найти
Решение:
По теореме Виета уравнение 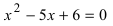
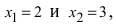
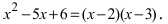
Метод замены переменной интегрирования
Данный метод основан на формуле
Метод замены переменной интегрирования применяется в двух случаях:
а) Если аргумент функции отличается от простого аргумента х, то этот сложный аргумент принимается в качестве новой переменной интегрирования t.
Пример:
Вычислить
Решение:
Так как показатель степени экспоненты отличается от простого аргумента х, то этот показатель степени принимаем в качестве новой переменной интегрирования, т.е.
Замечание: После нахождения первообразной с новой переменной интегрирования надо обязательно вернуться к старой переменной интегрирования.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом степенной функции и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом функции синус и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е. 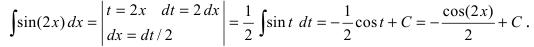
Пример:
Найти
Решение:
В подынтегральном выражении содержится элементарная функция tgx и в качестве множителя при dx присутствует ее первая производная 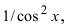
Пример:
Найти
Решение:
Данный пример объединяет первый метод с методом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых применяются два случая замены переменной интегрирования
Замечание: Умение отыскивать подходящую замену вырабатывается в процессе многократных упражнений, однако можно указать ряд случаев, когда можно сразу увидеть необходимую замену переменной интегрирования при анализе подынтегрального выражения, например, 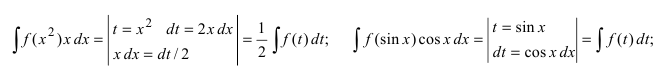
Метод интегрирования по частям
Интегрирование по частям основано на использовании формулы дифференциала от произведения двух функций 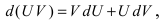
Таким образом, для неопределенного интеграла формула интегрирования по частям имеет вид:
Для того чтобы знать, какую из функций принимать за U (все остальное в подынтегральном выражении принимается за dV), рассмотрим наиболее часто встречающиеся случаи:
1. 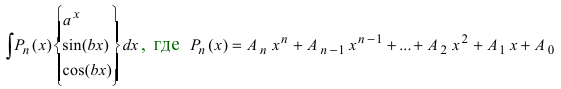
В этом случае
Замечание: Для нахождения функции dU используют определение дифференциала функции. При вычислении функции V интегрируют выражение dV, при этом постоянная интегрирования полагается равной нулю (С = 0). После выполнения этих действий применяют формулу интегрирования по частям.
Пример:
Вычислить
Решение:
Применим метод интегрирования по частям
Замечание: Из приведенного примера видно, что при необходимости метод интегрирования по частям применяется повторно.
2. Для интегралов вида
Пример:
Вычислить
Решение:
Действуя согласно методике, получим
3. Для интегралов вида 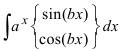
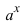
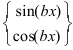
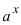
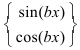
Пример:
Найти
Решение:
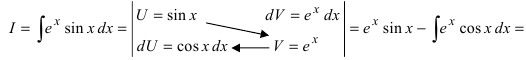
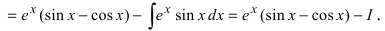
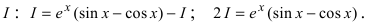
4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.
Пример:
Найти
Решение:
Неопределенный интеграл
Определение 1. Пусть Δ − промежуток действительной оси. Функция y=F(x) называется первообразной для функции y=f(x) на промежутке Δ, если F(x) − дифференцируема на Δ и 
Пример:
а) F(x)=x − первообразная для 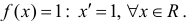
б) 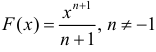
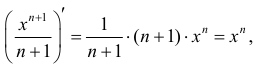
в) 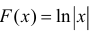
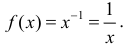
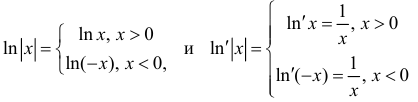
Замечание. Первообразная функция определена не однозначно. А именно,
F(x) = x+C , где С – любая константа также будет первообразной для 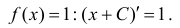
В общем случае верна теорема:
Теорема 1. Две дифференцируемые на промежутке Δ функции 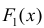
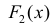
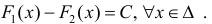
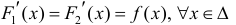
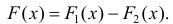
Тогда 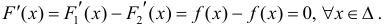
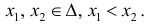
По теореме Лагранжа (теорема 4 § 12): 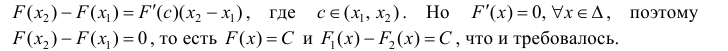
Достаточность. 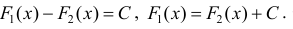
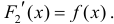
Тогда 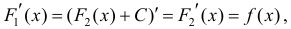
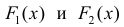
для одной и той же функции y=f(x), что и требовалось доказать.
Определение 2. Множество всех первообразных для функции y=f(x) на промежутке Δ называется неопределенным интегралом от функции f(x) и обозначается 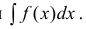
Если F(x) — одна из первообразных, то , согласно теореме 1, 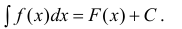
Свойства неопределенного интеграла
- Если ( ) F x — дифференцируема на Δ , то
(3) или
(4) здесь под записью
подразумеваем одну из первообразных.
- Если f (x) имеет первообразную на Δ, то λf(x) также имеет первообразную на Δ и ,если λ ≠ 0, то
(5)
- Если
имеют первообразную на Δ , тогда
также имеет первообразную на Δ и:
(6)
Свойства 1 – 4 легко выводятся из определения первообразной и интеграла
и соответствующих свойств производной.
Докажем, например, свойство 3.
Пусть F (x) — первообразная для f (x) на промежутке Δ. Тогда 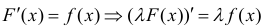
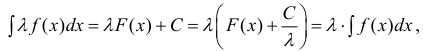
Из определений 1,2 следует, что интегрирование – действие обратное
дифференцированию (находится функция, производная которой равна данной).
Таблица интегралов
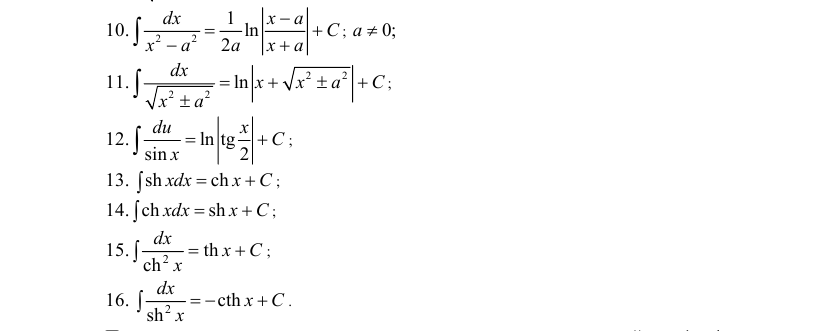
При вычислении интегралов в простых случаях применяют свойства 1 – 4.
Пример:
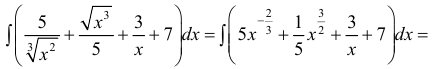
Пример:
Теорема 1. Если y=f(x) — непрерывна на промежутке Δ , то для нее ∃ первообразная функция y = F(x) на этом промежутке.
Замена переменной в неопределенном интеграле
Теорема 1. Пусть функция y = F(t) — первообразная для функции y = f(t) на промежутке 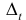
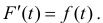
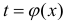
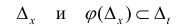
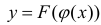
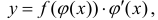
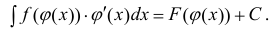
Доказательство. 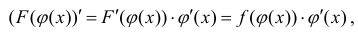
Замечание. Формулу (1) можно переписать в виде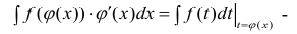
формула интегрирования с помощью подстановки 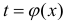
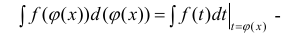
Формула интегрирования с помощью поднесения под дифференциал, когда
подынтегральную функцию 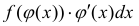
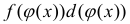
занося 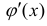
Пример:
Пример:
Пример:
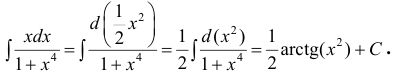
При поднесении под дифференциал можно использовать свойства
дифференциала (см. § 6) 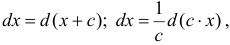
Пример:
Пример:
Пример:
Иногда в формуле (2) легче вычислять левую часть, чем правую:
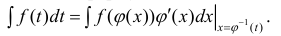
Формула (5) – формула интегрирования с помощью замены переменной 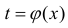
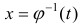
Пример:
Интегрирование по частям в неопределенном интеграле
Теорема 1. Пусть функция u(x) и v(x) – дифференцируемы на промежутке Δ и на этом промежутке 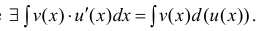
∃ и 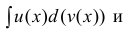
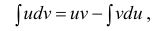
Доказательство. 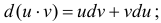
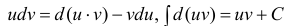
Пример:
Пример:
Замечание.
- При интегрировании выражений вида:
— многочлен степени n полагают:
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
- При интегрирования выражений вида:
полагают:
(
— многочлен). После интегрирования по частям интеграл упрощается.
Пример:
Пример:
Таким образом, проинтегрировав дважды по частям, получили уравнение,
содержащее 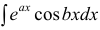
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определённый интеграл
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник

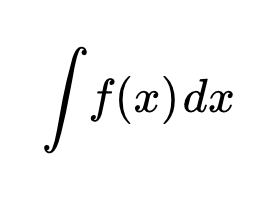
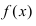
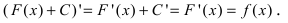
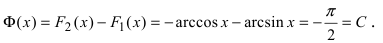
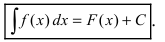
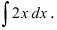
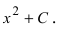
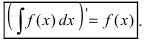
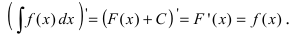
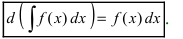
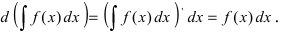
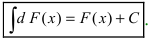
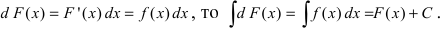
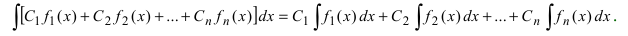
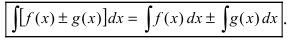
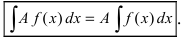
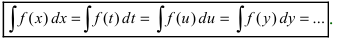
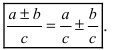
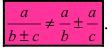
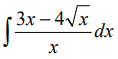
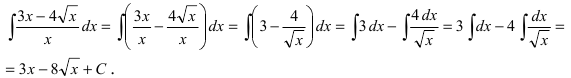
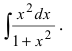
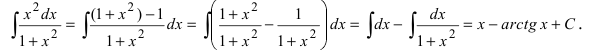
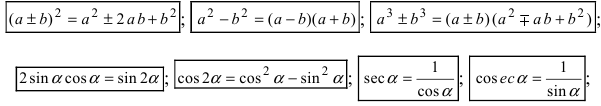
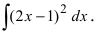
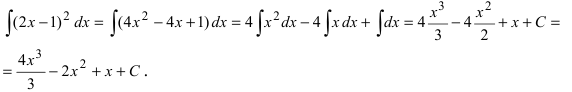
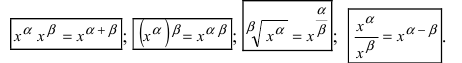
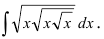
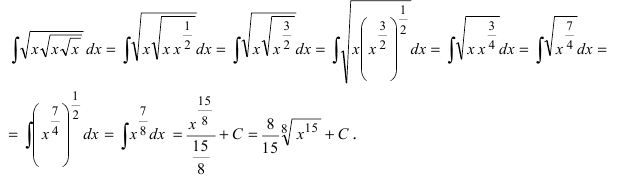
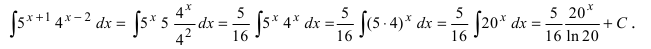
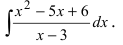
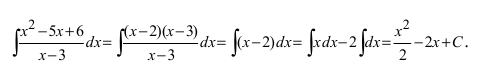
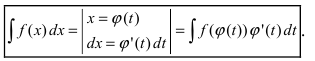
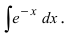
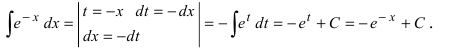
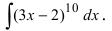
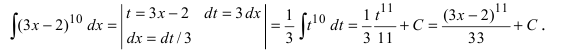
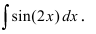
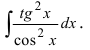
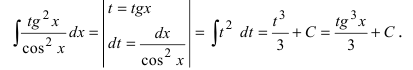
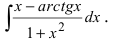
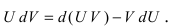
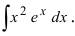
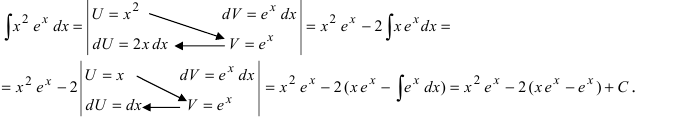
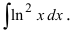
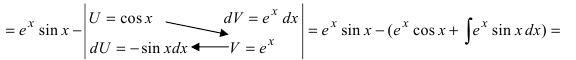
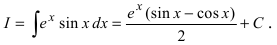
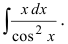
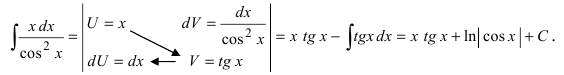
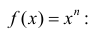
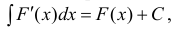 (3) или
(3) или 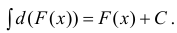
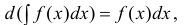 (4) здесь под записью
(4) здесь под записью 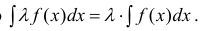 (5)
(5)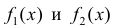 имеют первообразную на Δ , тогда
имеют первообразную на Δ , тогда 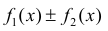 также имеет первообразную на Δ и:
также имеет первообразную на Δ и: 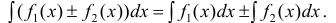 (6)
(6)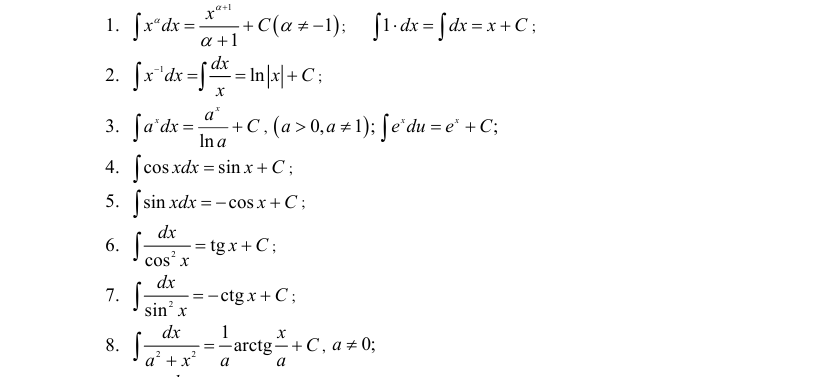
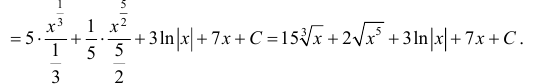
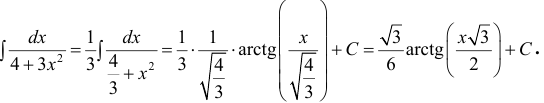
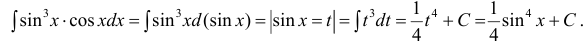
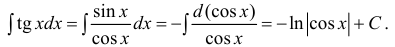
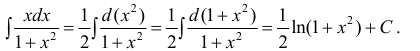
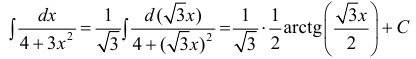
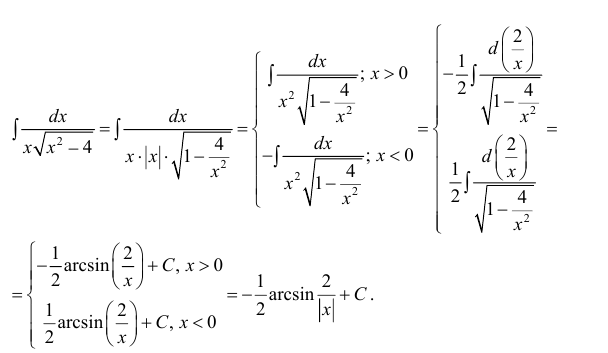
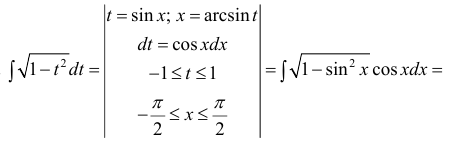
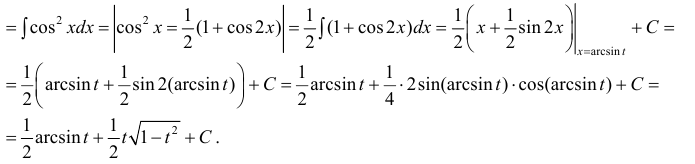
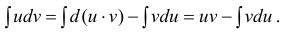
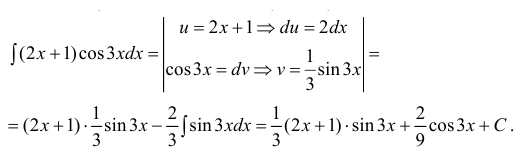
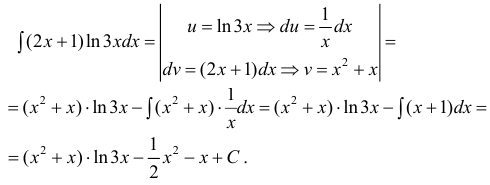
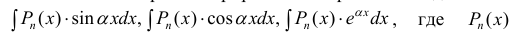 — многочлен степени n полагают:
— многочлен степени n полагают: 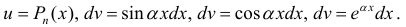 После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).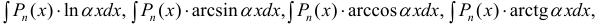
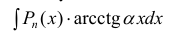 полагают:
полагают: 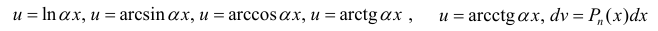 (
(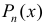 — многочлен). После интегрирования по частям интеграл упрощается.
— многочлен). После интегрирования по частям интеграл упрощается.