Способы хранения графа python

работа с графами в Python

Table of Contents

1 Граф

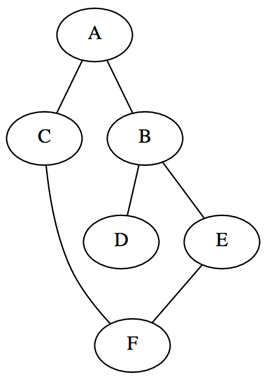
Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

• Помечаем текущую вершину как посещённую
• Исследуем каждую соседнюю вершину не включённую в список уже посещённых
• Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

• Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

3 DFS Paths — поиск пути между двумя вершинами

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

Источник

Русские Блоги

Реализация графа Python

1. Определение графа

С математической точки зрения, граф состоит из множества вершин V и множества ребер E, где каждое ребро в E соединяет две вершины в V. Вершины и ребра могут быть помечены или не помечены. Когда ребра помечены числами, эти числа можно рассматривать как веса, а граф называется взвешенным графом.

• Она достижима из одной вершины в другую тогда и только тогда, когда перед двумя вершинами есть путь. Длина пути — это количество сторон пути.
• Если есть путь от каждой вершины графа к каждой другой вершине, граф соединен.
• Если есть ребро, соединяющее каждую вершину графа со всеми остальными вершинами, граф является полным.

• Соседство: если ребро соединяет две вершины, мы говорим, что две вершины смежны, также называемые соседями.
• Путь: последовательность ребер от одной вершины графа к другой вершине.
• Степень: степень вершины равна количеству соединяющих ее ребер.

Во-вторых, представление графа

Чтобы представить граф, нам нужен удобный способ хранения вершин и ребер, соединяющих вершины.Обычные представления: матрица смежности и список смежности.

2.1 Смежная матрица

Как показано на рисунке ниже, два столбца с цифрами и буквами в левой части матрицы соответственно содержат позицию строки и метку позиции вершины, которая рассматривается как исходная вершина потенциального ребра. Цифры и буквы над матрицей указывают целевые вершины потенциальных ребер. График на рисунке ниже имеет 4 ребра. Следовательно, как показано на рисунке 12.8, только 4 из 16 ячеек матрицы заполнены 1, то есть ячейками (1,0), (1,2), (1, 3), (3,2). Если график неориентированный, то остальные 4 ячейки, заполненные единицами, считаются повторениями каждой стороны (как показано на рисунке 12.9).

Если у ребра есть вес, значение веса может занимать ячейку матрицы. Тогда ячейки, у которых нет краев, должны иметь некоторые значения, и эти значения не находятся в пределах допустимого диапазона значений веса. Если вершины помечены, метки можно хранить в одном одномерном массиве.

2.2 Список смежности

Список смежности означает, что информация, относящаяся к графу, хранится в массиве списков, который может быть реализован с использованием связанного списка или списка на основе массива.

Когда у ребра есть вес, вес также можно включить в качестве другого поля данных узла, как показано на рисунке 12.12.

В-третьих, обход графа

Алгоритм обхода графа начинается с заданной вершины и перемещается наружу, чтобы исследовать путь к соседним вершинам. Итеративная (нерекурсивная) версия этого алгоритма планирует доступ ко всем вершинам в едином временном наборе. Тип коллекции, используемый для планирования, влияет на порядок посещения вершин.

При обходе графа обычно используются два порядка доступа к вершинам:

• Обход в глубину, который использует стек как коллекцию в общем алгоритме. Процесс обхода с использованием стека сначала углубится в график, а затем вернется к другому пути. Другими словами, использование стека приведет к тому, что алгоритм перейдет от одной вершины к одному из своих соседей, затем к другому соседу своих соседей и т. Д.
• Обход в ширину (обход в ширину) использует очередь как коллекцию в общем алгоритме.Процесс обхода с использованием очереди посещает каждую вершину, смежную с данной вершиной, а затем углубляется в граф.

В-четвертых, реализация множества графов

4.1 Методы класса LinkedDirectedGraph:

4.2 Код реализации

4.2.1 Создайте абстрактный класс коллекции и сохраните его как файл abstractcollection.py

4.2.2 Создайте набор графиков и сохраните его как файл graph.py

4.2.3 Тестовый файл

4.2.3.1 Тест неориентированного графа

Источник

Способы хранения графа python

Начнём с выяснения, зачем же нам нужны графы, какие вещи в реальном мире они позволяют изучать. Посмотрим на карту метрополитена города Киева:

Теперь взглянем на участок Москвы с автомобильными дорогами (скриншот сделан с сайта Яндекс.Карты).

Далее, обратим внимание на генеалогическое древо славянской языковой группы.

Наконец, посмотрим на пример цепи питания в биологии.

Что общего у всех этих картинок? Главное, что на них изображено — это объекты и связи между ними. В теории графов все такие картинки называются графами. Графы состоят из вершин и рёбер. Так, в графе киевского метрополитена станции считаются вершинами, а перегоны между ними — рёбрами. В графе цепи питания биологические виды являются вершинами, и направленное ребро проведено от одного вида к другому тогда, когда первый вид является пищей для второго.

Итак, графом называется набор вершин и набор рёбер. Каждое ребро соединяет две вершины.

Степенью вершины называется количество рёбер, концом которых она является. Например, в графе метрополитенов большинство станций имеют степень 2, а конечные станции имеют степень 1. В графе славянской языковой группы вершина «западнославянский язык» имеет степень 4.

2. Виды графов и пути в графах

Подумаем, нужно ли считать граф дорог ориентированным. Пусть мы пишем программу, которая по графу дорог находит автомобильный маршрут между двумя точками в городе. Поскольку в городе бывают улицы с односторонним движением, то наша программа должна это учитывать. Значит, на каждом ребре нужно хранить направление — возможное направление проезда по ребру. Если по дороге можно проехать в обе стороны, то рисуют два ребра со стрелками в разные стороны.

Путём в графе называется любая последовательность вершин, в которой каждые две соседние вершины соединены ребром. На рисунке выше A → C → B → G — это путь из вершины A в вершину G. Есть и более короткий путь из A в G: путь A → B → G. Длиной путиназывается количество рёбер в нём. Таким образом, кратчайший путь из A в G имеет длину 2.

Циклом в графе называют путь, у которого начальная и конечная вершина совпадают. На рисунке выше путь A → C → B → D → A является циклом.

(Осторожно, сейчас мы введём очень сложное понятие.) Компонентой связностинеориентированного графа называется любой набор его вершин, который удовлетворяет следующим двум свойствам:

1. между любыми двумя вершинами набора существует путь;
2. набор нельзя расширить, добавив в него ещё хотя бы одну вершину, чтобы при этом осталось верным свойство 1.

Всякий неориентированный граф разбивается на свои компоненты связности. На рисунке выше имеются три компоненты связности: , и . Граф, у которого только одна компонента связности, называется связным. Граф, у которого более одной компоненты связности, называется несвязным. На рисунке выше изображён несвязный граф.

В ориентированном графе путём называется любая последовательность вершин, в которой соседние вершины соединены ребром, и это ребро идёт «слева направо» (в нужную сторону). Например, на рисунке ниже A → B → C → D является путём, а A → D → C → B — не является (потому что в графе нет рёбер A → D и C → B).

В ориентированном графе некоторые понятия, которые мы ввели для неориентированных графов, имеют свои аналоги. Например, наряду с понятием «степень вершины», в ориентированных графах используются понятия полустепень захода (количество рёбер, входящих в вершину) и полустепень исхода (количество рёбер, исходящих из вершины). На рисунке выше вершина D имеет полустепень захода 1 и полустепень исхода 3.

Наконец, отметим, что в некоторых графах допустимы ситуации, изображённые на следующей картинке.

3. Деревья

Деревья обладают рядом особых свойств. Например, в дереве между любыми двумя вершинами существует единственный простой путь. Действительно, если бы между какими-нибудь двумя вершинами существовало более одного простого пути, то отсюда бы следовало, что в графе есть простой цикл.

Ещё одно удивительное свойство деревьев — это связь между количеством вершин и количеством рёбер. Договоримся обозначать буквой V количество вершин (от англ. vertex «вершина»), а буквой E — количество рёбер (от англ. edge «ребро»). Например, у дерева на рисунке выше V = 11, E = 10. Мы видим, что для графа на рисунке E = V − 1.

Чтобы понять, всегда ли это будет верно, рассмотрим висячие вершины. Висячей вершинойназывается вершина степени 1. На рисунке выше висячими являются вершины A, C, F, G, H, J и K. Заметим, что в дереве, в котором есть хотя бы две вершины, всегда есть хотя бы одна висячая вершина. Действительно, выберем произвольную вершину дерева и пойдём из неё гулять по рёбрам дерева в произвольном направлении, не возвращаясь назад. Поскольку циклов в дереве нет, то с каждым шагом мы будем посещать всё новые и новые вершины и в какой-то момент придём в вершину, из которой никуда пойти нельзя. Эта вершина и будет висячей.

Теорема. В любом дереве E = V − 1.

Доказательство. Как мы выяснили, если в дереве хотя бы две вершины, то в нём есть хотя бы одна висячая вершина. Выберем её и удалим из графа её и ребро, за которое она присоединена к графу. При этом количество вершин и рёбер уменьшится на единицу. С новым графом проделаем ту же операцию. В конце концов, когда мы удалим всё, что можно, мы получим граф из одной вершины. Для него V = 1, E = 0, т.е. E = V − 1. Значит, и в исходном дереве выполнялось E = V − 1. ▮

4. Как хранить граф в программах

Второй способ, которым можно хранить этот граф, — это структура данных «матрица смежности». Матрица смежности — это квадратная таблица, в которой на пересечении строки i и столбца j стоит 1, если в графе есть ребро из вершины i в вершину j, и стоит 0, если такого ребра нет.

Заметим, что матрица смежности неориентированного графа всегда симметрична относительно главной диагонали. Главная диагональ в матрице идёт из левого верхнего угла в правый нижний.

Наконец, третий способ, который часто используют для представления графов, — это структура данных «списки смежности». В списках смежности для каждой вершины хранится список всех её соседей.

Для хранения ориентированных графов применяются те же структуры данных, с разумными поправками:

• в списке рёбер ребро хранится в виде [начало, конец] ;
• в матрице смежности ребро из i в j означает adjacency_matrix[i][j] == 1 , и если обратного ребра в графе нет, то будет верным равенство adjacency_matrix[j][i] == 0 ;
• в списках смежности для каждой вершины хранится, в какие вершины из неё исходят рёбра.

Источник

Способы хранения графа python

Одна и та же математическая формулировка возникает в разных практических задачах. Пусть, например, мы хотим назначить даты экзаменов так, чтобы никому не надо было сдавать два экзамена в один день, и при этом хотим занять поменьше дней. Заведём вершину для каждого экзамена и соединим две вершины ребром, если хотя бы один студент сдаёт оба экзамена. Раскрасив граф в минимальное число цветов, получим оптимальное расписание (экзамены одного цвета назначаются на один день).

Граф задаётся множеством вершин V и множеством рёбер E, соединяющих пары вершин. (Английская терминология: вершина называется vertex или node, а ребро — edge.)

В примере с картой V = , а рёбра из E соединяют страны, граничащие друг с другом (в частности, E содержит рёбра <1, 2>, <9, 11>и <7, 13>). Отношение «быть соседом» симметрично, так что ребро из x в y возникает одновременно с ребром из y в x. Поэтому мы записываем ребро, соединяющее x с y, как множество: <x, y>. Такие рёбра называются неориентированными (undirected), а соответствующий граф — неориентированным графом (undirected graph).

Бывают и несимметричные отношения, и их изображают ориентированными рёбрами (directed edges). В ориентированном графе наличие ребра из x в y не гарантирует наличие ребра из y в x. Ориентированное ребро из x в y будем обозначать (x, y). Можно считать «всемирную паутину» (World Wide Web) ориентированным графом: из вершины u идёт ориентированное ребро в вершину v, если на странице u есть ссылка на страницу v. В этом графе миллиарды вершин и рёбер, так что алгоритмы, с ним работающие, должны быть быстрыми (к счастью, такие алгоритмы есть — многое можно сделать за линейное время).

Корневые деревья

Начнём знакомство с графами с самыми простыми с точки зрения их структуры графами — корневыми деревьями. Напомним, деревом называется связный граф без циклов. Дерево с отмеченной вершиной — корнем — называется корневым деревом. В отличие от обычных деревьев, корневые обычно рисуют корнем к верху.

Итак, отмеченную вершину называют корнем. Как известно, в дереве между любыми двумя вершинами существует ровно один путь. Возьмём любую вершину и соединим её путём с корнем. Все вершины в этом пути, кроме исходной, называются её предками (ancestor). Вершина, следующая в этом пути за исходной, называются её родителем (parent). Корень — это единственная вершина в дереве, у которой нет ни родителей, ни предков вообще.

На этой картинке Grace, Alice и Jake являются предками Luca, Caitlin и Jake — предками Ben. Jake является общим предком Luca и Ben (а заодно и общим предком вообще всех вершин).

Если вершина А является предком вершины Б, то Б называется потомком (descendant) А. Для данной вершины А множеством её потомков являются все вершины, не совпадающие с А, путь из которых к корню проходит через А. Аналогично, если вершина А — родитель вершины Б, то вершина Б называется сыновьей (child) для А.

Здесь уже всё понятно, у каждой вершины, кроме корня, есть единственный предок.

Luca — единственный потомок Grace. У Caitlin четыре потомка — Ben, Megan, Eva и Harry. И наконец у Sean нет потомков.

Вершины, у которых общий родитель, называются братьями (sibling).

И наконец вершины, у которых нет потомков, называются листьями.

Как хранить деревья в программе

Например, дерево с картинок выше будем хранить так: Такой способ хранения, вообще говоря, избыточен. По словарю children можно восстановить словарь parents и наоборот. И по любому из этих словарей можно найти корень. Однако он достаточно удобен.

Источник