Способы графического задания прямой линии
Для определения положения прямой в пространстве существуют следующие методы:
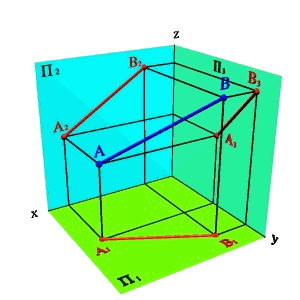
1.Двумя точками (А и В).
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
| Рисунок 15.Определение положения прямой по двум точкам | |||
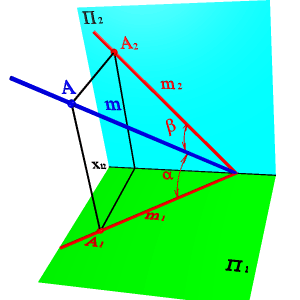
Обозначим углы между прямой и плоскостями проекций через α — с плоскостью П1, β — с плоскостью П2, γ — с плоскостью П3 и тогда получим:
Частный случай | A 1 B 1 | = | A 2 B 2 | = | A 3 B 3 | при таком соотношении прямая образует с плоскостями проекций равные между собой углы a = b = g = 35 0 , при этом каждая из проекций расположена под углом 45 0 к соответствующим осям проекций.
2. Двумя плоскостями ( a ; b ) .
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [ А1 В1 ] и [ A 2 B 2 ] . П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис. 16 а), линией их пересечения будет прямая заданная отрезком [ АВ ] , проекциями которой являются отрезки [ А1 В1 ] и [ А2 В2 ] .
 |  | /pic1.gif) |
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
| Рисунок 15.Определение положения прямой по двум точкам | |||
Обозначим углы между прямой и плоскостями проекций через α — с плоскостью П1, β — с плоскостью П2, γ — с плоскостью П3 и тогда получим:
Частный случай | A 1 B 1 | = | A 2 B 2 | = | A 3 B 3 | при таком соотношении прямая образует с плоскостями проекций равные между собой углы a = b = g = 35 0 , при этом каждая из проекций расположена под углом 45 0 к соответствующим осям проекций.
2. Двумя плоскостями ( a ; b ) .
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [ А1 В1 ] и [ A 2 B 2 ] . П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис. 16 а), линией их пересечения будет прямая заданная отрезком [ АВ ] , проекциями которой являются отрезки [ А1 В1 ] и [ А2 В2 ] .
 |  | /pic1.gif) |
 |  | ||||||||||||||||||||||||||||||||||||||
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
| Рисунок 15.Определение положения прямой по двум точкам | |||
Обозначим углы между прямой и плоскостями проекций через α — с плоскостью П1, β — с плоскостью П2, γ — с плоскостью П3 и тогда получим:
Частный случай | A 1 B 1 | = | A 2 B 2 | = | A 3 B 3 | при таком соотношении прямая образует с плоскостями проекций равные между собой углы a = b = g = 35 0 , при этом каждая из проекций расположена под углом 45 0 к соответствующим осям проекций.
2. Двумя плоскостями ( a ; b ) .
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [ А1 В1 ] и [ A 2 B 2 ] . П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис. 16 а), линией их пересечения будет прямая заданная отрезком [ АВ ] , проекциями которой являются отрезки [ А1 В1 ] и [ А2 В2 ] .
 |  | /pic1.gif) |
 |  | |||||||||||||||||||
 |  |  |  |
 | |||
 | |||
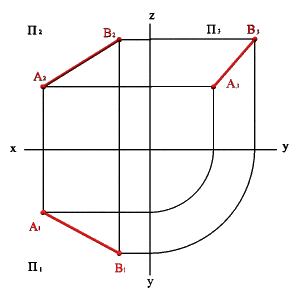
| а) модель | б) эпюр | ||
| Рисунок 15.Определение положения прямой по двум точкам | |||
Обозначим углы между прямой и плоскостями проекций через α — с плоскостью П1, β — с плоскостью П2, γ — с плоскостью П3 и тогда получим:
Частный случай | A 1 B 1 | = | A 2 B 2 | = | A 3 B 3 | при таком соотношении прямая образует с плоскостями проекций равные между собой углы a = b = g = 35 0 , при этом каждая из проекций расположена под углом 45 0 к соответствующим осям проекций.
2. Двумя плоскостями ( a ; b ) .
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
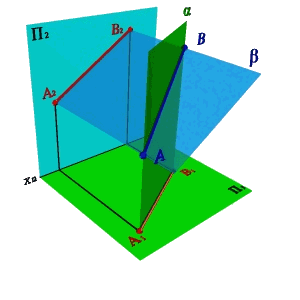
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [ А1 В1 ] и [ A 2 B 2 ] . П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис. 16 а), линией их пересечения будет прямая заданная отрезком [ АВ ] , проекциями которой являются отрезки [ А1 В1 ] и [ А2 В2 ] .
 |  | /pic1.gif) |
 |  |




