Способы графического задания плоскостей
Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии (рис. 41 );
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
3. двумя пересекающимися прямыми (рис.43);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
4. двумя параллельными прямыми (рис.44);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a П1, фронтальный a П2 и профильный a П3 следы.
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
Следы плоскости общего положения пересекаются попарно на осях в точках a x , a y , a z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
Источник
Способы графического задания плоскостей
Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии (рис. 41 );
 | 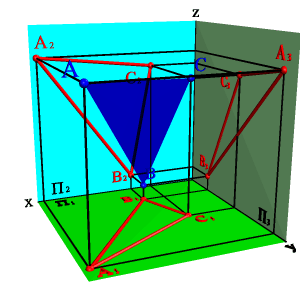 | 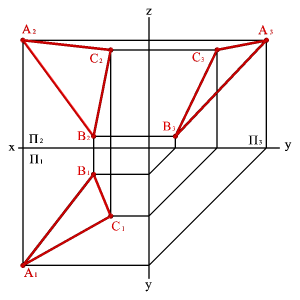 |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);
 | 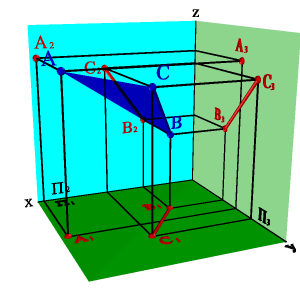 | 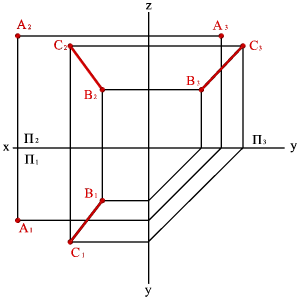 |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
3. двумя пересекающимися прямыми (рис.43);
 | 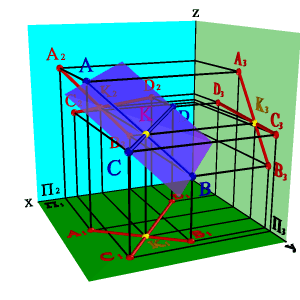 | 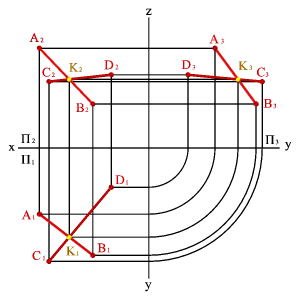 |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
4. двумя параллельными прямыми (рис.44);
 | 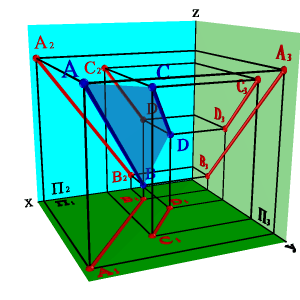 | 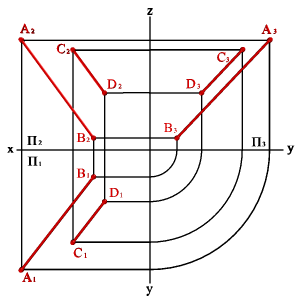 |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
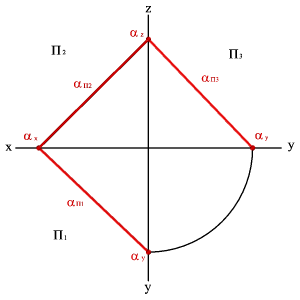
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a П1, фронтальный a П2 и профильный a П3 следы.
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
Следы плоскости общего положения пересекаются попарно на осях в точках a x , a y , a z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
Источник
Способы графического задания плоскостей
Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии (рис. 41 );
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
3. двумя пересекающимися прямыми (рис.43);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
4. двумя параллельными прямыми (рис.44);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a П1, фронтальный a П2 и профильный a П3 следы.
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
Следы плоскости общего положения пересекаются попарно на осях в точках a x , a y , a z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
Источник




