Способы графического представления колебаний

Учебники

Журнал «Квант»

Общие

Графическое представление гармонических колебаний. Векторные диаграммы

Наиболее часто употребляются три способа графического представления колебаний.

1. Задание графика колебаний х = f(t) в прямоугольной системе координат. По оси абсцисс откладывается время t, а по оси ординат — значение изменяющейся величины х (смещения, скорости, ускорения и др.). Для гармонических колебаний этот график — косинусоида (см. рис. 13.3) или синусоида.

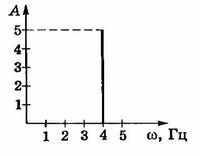
2. Спектральный способ. По оси ординат откладывается амплитуда, а по оси абсцисс — частота гармонических колебаний. Так, например колебательный процес \(x = 5 \cos 4t\) (м) будет представлен в этом случае вертикальным отрезком прямой длиной 5 м, проведенным от точки с координатой \(\omega\) = 4 Гц на оси абсцисс (рис. 13.4). Этот способ не дает никакой информации о фазе колебания.

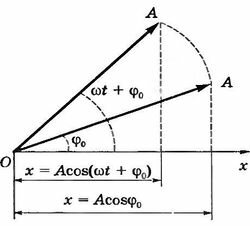
3. Способ векторных диаграмм. Пусть величина х изменяется со временем по закону \(x = A \cos(\omega t + \varphi_0).\)

На плоскости выбирают произвольно направленную координатную ось Ох. Из начала координат под углом \(\varphi_0,\) равным начальной фазе колебаний, проводят вектор \(\vec A\), модуль которого равен амплитуде гармонического колебания A (рис. 13.5). Если вектор \(\vec A\) вращается вокруг точки О с постоянной угловой скоростью \(

\omega\) против часовой стрелки, то угол \(\varphi\) между вращающимся вектором и осью Ох в любой момент времени определится выражением \(\varphi = (\omega t + \varphi_0).\) Проекция конца вектора \(\vec A\) будет перемещаться по оси Ох и принимать значения от —А до +А, а колеблющаяся величина будет изменяться со временем по закону \(x = A \cos (\omega t + \varphi_0).\)

Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды \(\vec A\), отложенного от произвольной точки оси под углом \(\varphi_0\), равным начальной фазе, и вращающегося с угловой скоростью \(

\omega\) вокруг этой точки.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 370-371.

Источник

Методы представления колебаний

Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.

1. Аналитический метод

Задаётся уравнение колебаний гармонического осциллятора

по которому и определяется смещение его от положения равновесия в любой момент времени.

2. Графический метод

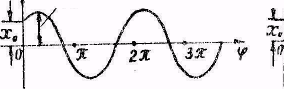
Рис.5.3

Строятся график гармонического колебания (рис.5.3) х=Аsin(ωt+φ₀). По оси абсцисс (ОХ) откладывается время t или фаза колебаний ωt+φ₀, по оси ординат (ОУ) – смещение х от положения равновесия.

3. Метод векторной диаграммы

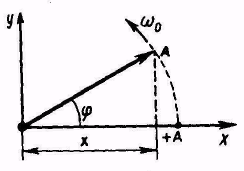
Рис.5.4

Этот метод состоит в следующем. Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде А колебания, а направление образует с осью х угол, равный начальной фазе колебания (рис. 5.4). Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора на ось х будет перемещаться в пределах от +А до -А, а колеблющаяся величина будет изменяться со временем по закону

x = Asin(ω₀t+φ₀), совершая гармоническое колебание.

§ 5.2.2 Скорость и ускорение колеблющейся точки

Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω₀t+φ₀) по времени:

(5.4)

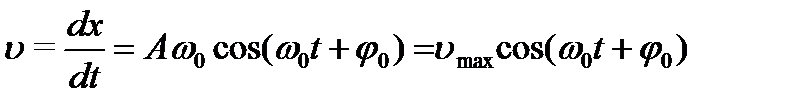
где υ_max = Аω₀ — максимальная скорость (амплитуда скорости).

На основании тригонометрических формул преобразуем (4.18):

(5.5)

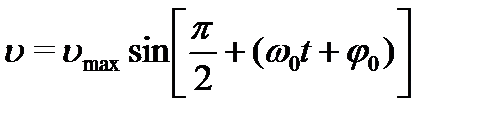
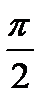
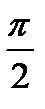
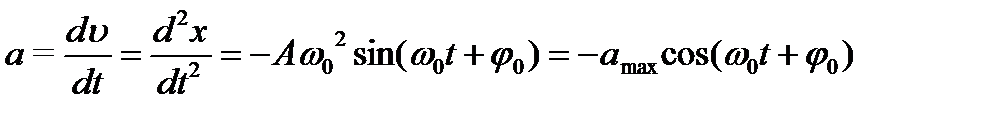
Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на больше фазы смещения, т.е. скорость опережает по фазе смещение на Продифференцировав (5.4), найдем ускорение:

(5.6)

где а_max = А ω₀ 2 — максимальное ускорение (амплитуда ускорения).

Вместо (5.5) запишем

Из сравнения (5.6) и (5.3) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.5.6, б) .

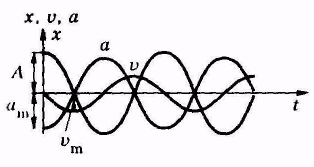
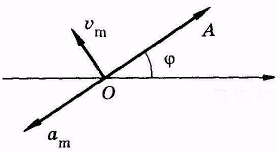
Рис.5.6

б )

а )

§ 5.2.3 Кинетическая и потенциальная энергии колебательного движения

Колеблющееся тело обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:

Кинетическая энергия тела, колеблющегося по гармоническому закону, вычисляют по формуле:

(5.9)

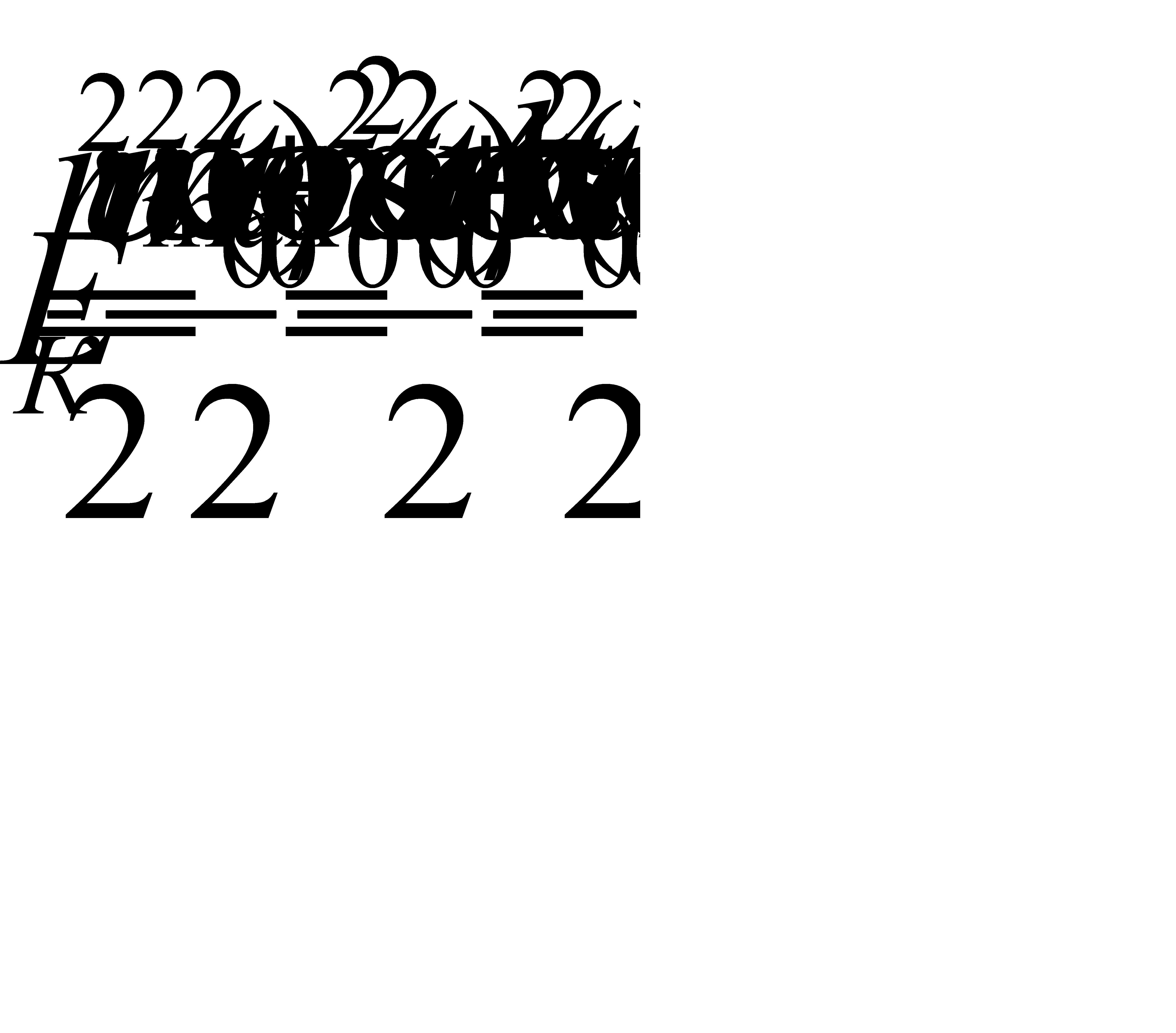
с учётом mω 2 = k

Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:

(5.10)

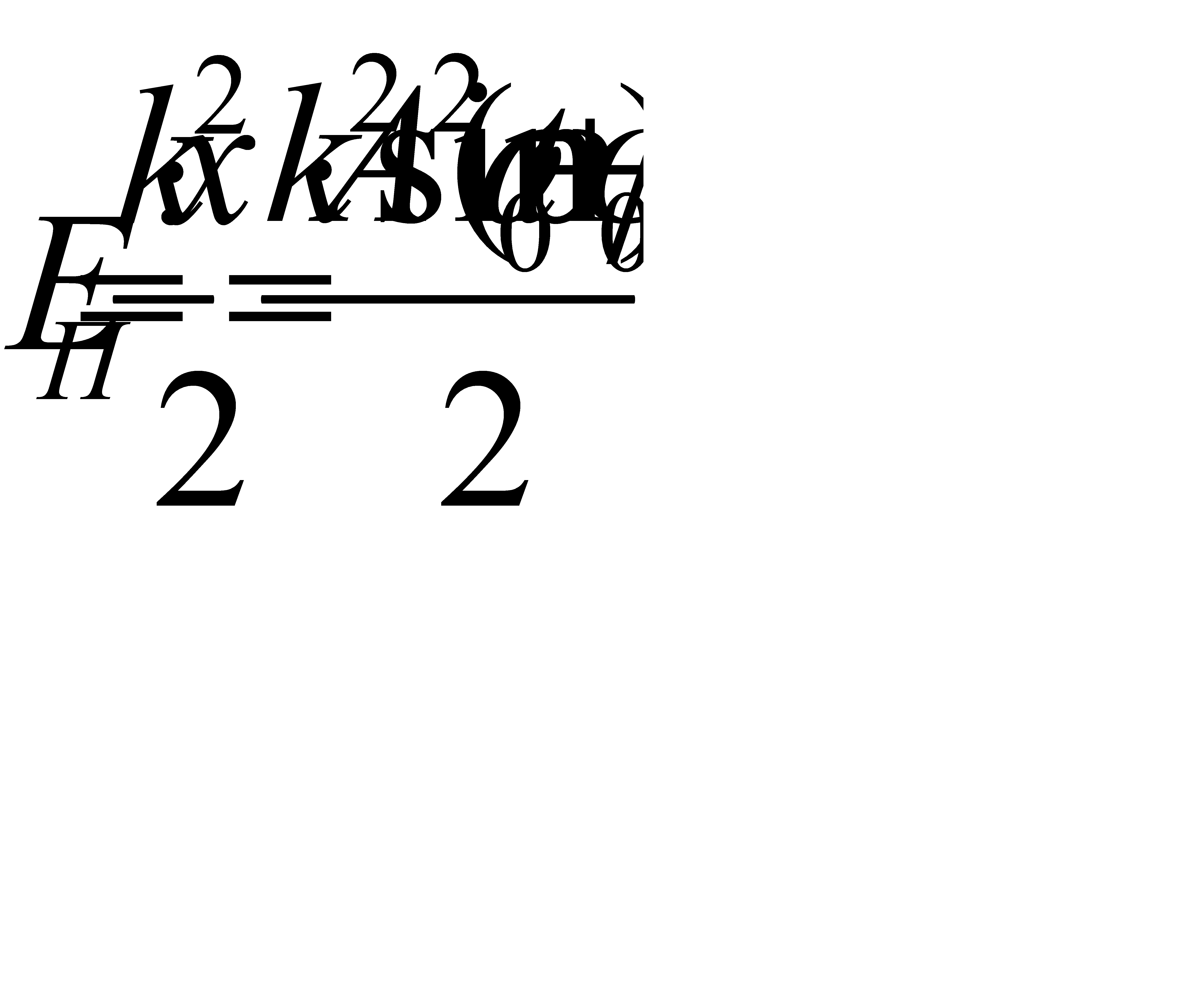
Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:

(5.11)

Полученное выражение показывает, что энергия колеблющегося тела от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.

При отсутствии сил трения полная механическая энергия системы не изменяется:

(5.12)

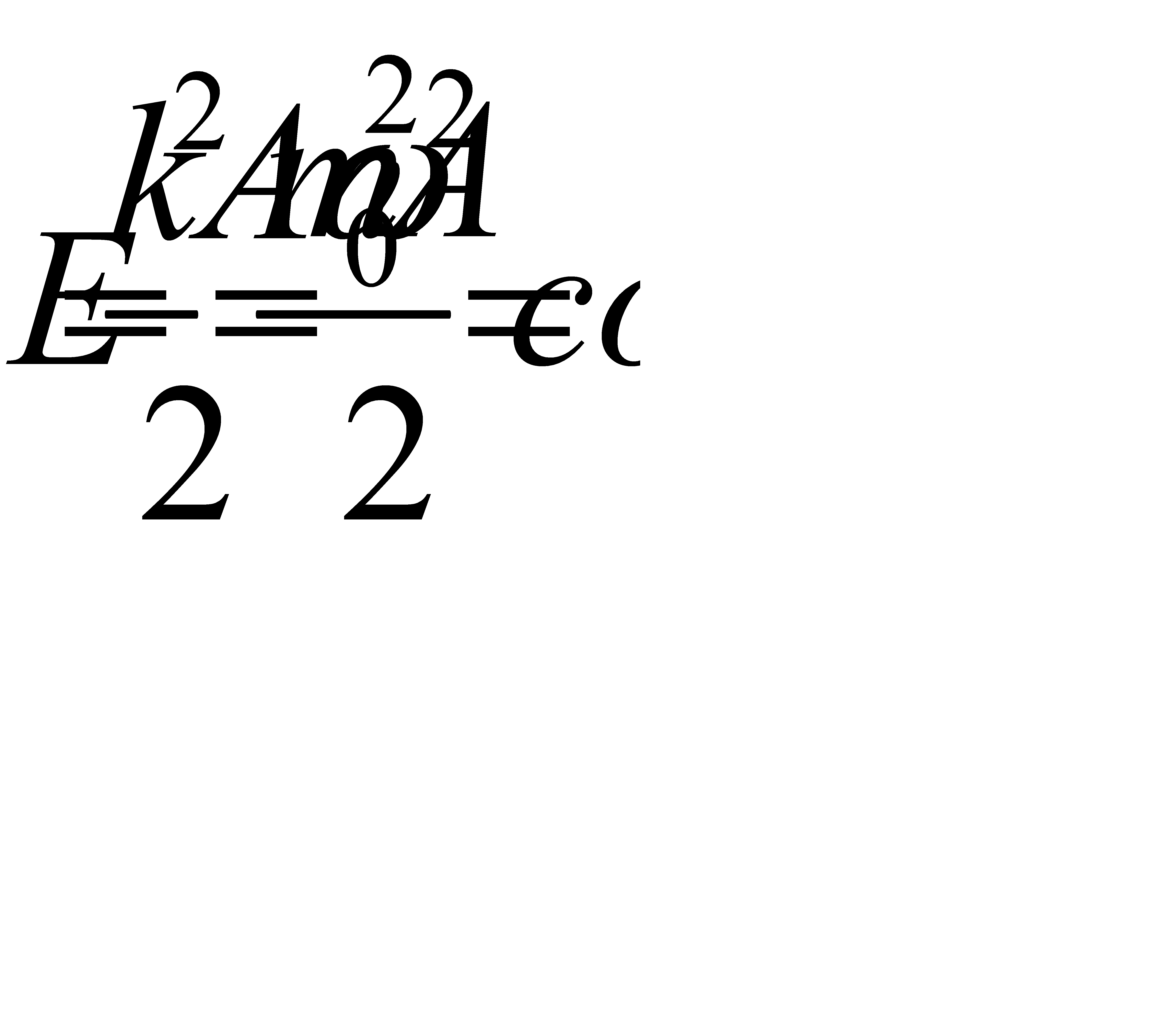
Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 5.7, а.

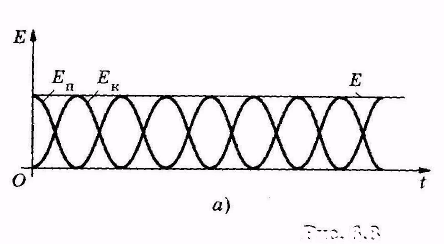
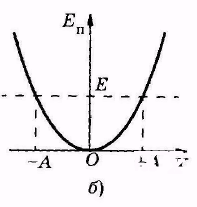
Рис.5.7

Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 5.7, б. Она определяется зависимостью 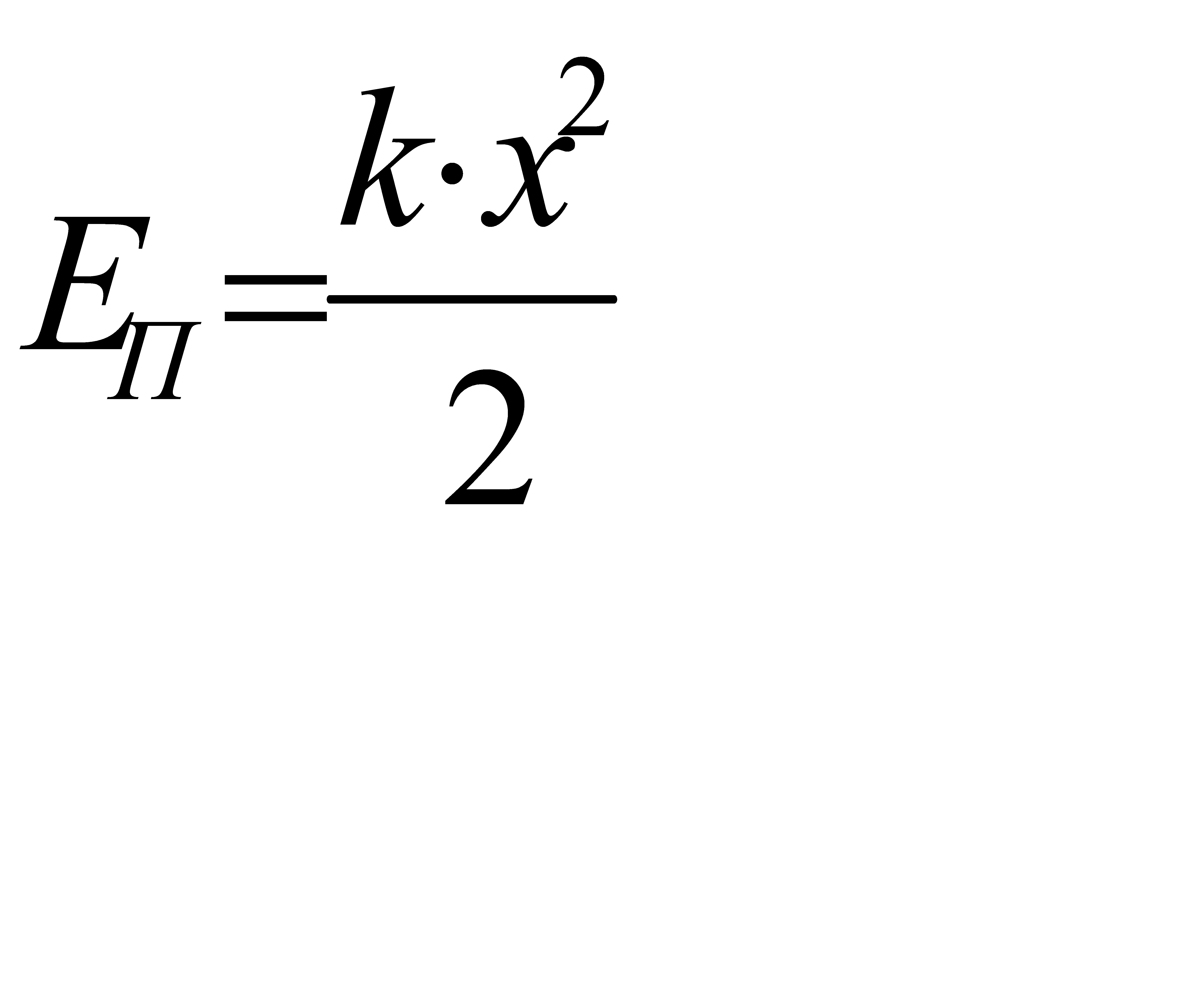. Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.

§6.2 Затухающие колебания

До сих пор мы рассматривали свободные колебания материальной точки без учёта сопротивления среды, в которой происходят эти колебания.

В реальных условиях на колеблющееся тело всегда действуют силы сопротивления (трения), в результате чего амплитуда с течением времени уменьшается и колебания становятся затухающими.

Рис.5.8

Пусть маятник колеблется в вязкой среде (рис.). В этом случае на осциллятор кроме возвращающей силы F_упр = -kx будет действовать ещё одна сила – сила сопротивления среды F_с. При малых колебаниях скорость движения осциллятора мала, поэтому сила сопротивления пропорциональна скорости и направлена в противоположную сторону:

(5.13)

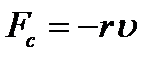
где r – коэффициент сопротивления среды, зависящий от плотности среды и геометрических размеров осциллятора; υ — относительная скорость движения осциллятора и среды.

Уравнение затухающих колебаний записывается в виде:

Выражение А=±А₀ е -δ t , есть переменная во времени амплитуда колебания; А₀— амплитуда в момент t = 0; ω -частота затухающих колебаний; φ₀-начальная фаза колебаний.

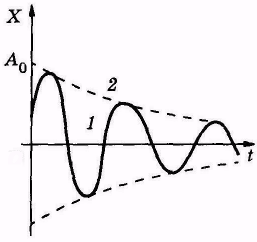
Рис. 6.9

График этой функции изображён на рисунке (кривая 1)пунктирнаялиния 2изображает ход убывания амплитуды. Материальная точка колеблется по закону синуса, но амплитуда колебания с течением времени уменьшается по экспоненте. Затухания происходят тем быстрее, чем больше δ, т.е. с увеличением внутреннего трения среды и уменьшением массы осциллятора.

Наглядной характеристикой затухания является отношение двух амплитуд, отличающихся по времени на период Т. Это соотношение называется декрементом затухания

(5.15)

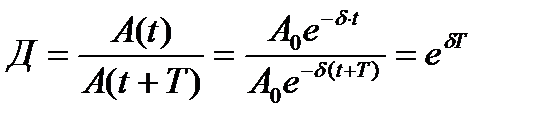
Прологарифмируем это выражение:

(5.16)

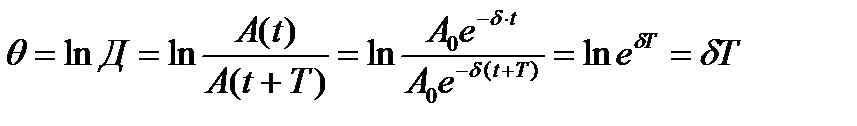
Значение θ=δТ называется логарифмическим декрементом затухания.

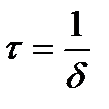
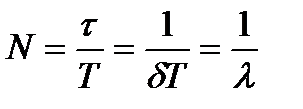
Время в течении которого амплитуда убывает в е раз, называется временем жизни колеблющейся точки. За время жизни τ система успевает совершить N колебаний.

(5.17)

Следовательно, логарифмический декремент затухания есть величина, обратная числу колебаний осциллятора за время его жизни.

Период затухающих колебаний зависит от коэффициента сопротивления rи определяется формулой:

(5.18)

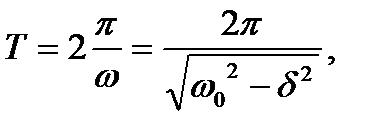
§6.3 Вынужденные колебания. Резонанс

Для того, чтобы колебания осциллятора были незатухающими, надо компенсировать потери энергии на преодоления сопротивления среды. Это можно сделать следующим способом. Пусть пружинный маятник с железным грузом находится в поле тяжести электромагнита, по обмотке которого проходит переменный ток:

Магнитная сила, действующая на маятник, меняется по тому же закону F_в=F₀sinωt. Эта периодически изменяющаяся внешняя сила, действующая на осциллятор, называется вынуждающей силой.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями.

Рис.6.11

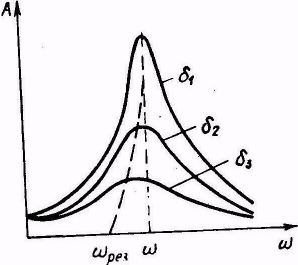
Зависимость амплитуды колебаний от частоты вынуждающей силы при различных δ приведены на рис. При ω → 0 амплитуда стремится к предельной величине, равной смещению осциллятора под действием постоянной силы F₀:

(6.42)

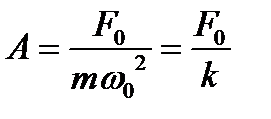
Когда частота вынуждающей силы приближается к частоте собственных колебаний осциллятора, амплитуда колебаний возрастает и при некоторой частоте достигает максимального значения. Это явление называется резонансом.

Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время. Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы — автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.

Классическим примером механической автоколебательной системы являются часы, в которых маятник (или баланс) является колебательной системой, пружина (или поднятая гиря) — источником энергии, а анкер — регулятором поступления энергии от источника в колебательную систему. Некоторые биологические системы (сердце, легкие) являются автоколебательными.

Дата добавления: 2015-12-08 ; просмотров: 1884 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник