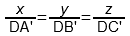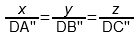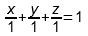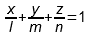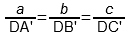Способы графического изображения фазовых диаграмм трехкомпонентных систем

Глава 10. Трехкомпонентные системы

10.1. Способы изображения состава трехкомпонентных систем

Для построения полной диаграммы состояния трехкомпонентной системы необходима система координат из пяти взаимно перпендикулярных осей, по которым откладываются температура, давление, мольные объемы различных фаз и мольные доли (или массовые проценты) двух компонентов в фазах. Реально построение такой диаграммы невозможно. Нельзя также построить проекцию этой диаграммы на четырехмерное пространство в осях: температура, давление, мольные доли двух компонентов. Лишь приняв какой-либо из параметров, например, температуру или давление, постоянным, можно построить трехмерную диаграмму, которая будет отображать зависимость числа и состава фаз в равновесных системах от исходного состава и от температуры (при постоянном давлении) или от давления (при постоянной температуре).

Часто для еще большего упрощения постоянными принимаются температура и давление одновременно. В этом случае на плоскости составов наносятся проекции сечения трехмерной диаграммы плоскостью T= const илиp= const. Двумерные диаграммы отражают различные состояния системы и фазовые переходы только при выбранных значенияхpиT.

При построении диаграммы состояния трехкомпонентной системы состав ее изображают на плоскости, а в перпендикулярном направлении откладывают температуру (p= const) или давление (T= const). Чаще используется первый вариант, так как давление в большинстве случаев при изучаемых превращениях остается постоянным или изменяется немного, а температурные изменения значительны.

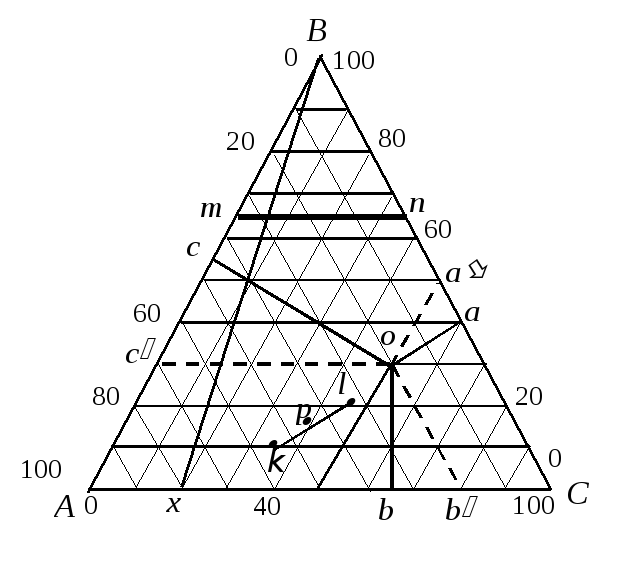
Рис.10.1. Треугольник Гиббса – Розебома для изображения состава трехкомпонентной системы

Состав трехкомпонентной системы обычно изображают, пользуясьтреугольником Гиббса – Розебома(рис. 10.1). Вершины равностороннего треугольника отвечают чистым компонентам (100%) A, B и C. Каждая из сторон треугольника позволяет описать составы двухкомпонентных систем A + B, B + C, A + C. Все точки внутри треугольника описывают составы трехкомпонентных систем.

Метод определения состава по Гиббсу основан на том, что сумма перпендикуляров, опущенных из любой точки равностореннего треугольника на каждую из сторон, равна высоте треугольника. Если принять, что высота треугольника соответствует 100 мольным (или массовым) процентам, то состав тройной системы можно выразить с помощью длин перпендикуляров. При этом содержанию данного компонента отвечает длина перпендикуляра, опущенного на сторону, противоположную соответствующей вершине треугольника. Например, точка оотвечает составу: 20% компонента A (отрезокоа), 30% компонента B (отрезокоb) и 50% компонента C (отрезокоc).

Длина перпендикуляра оценивается с помощью координатной сетки, покрывающей треугольник. Высоты треугольника делятся на 10 или 100 равных отрезков и через точки деления проводятся три группы параллельных прямых так, что каждая группа перпендикулярна соответствующей высоте треугольника, при этом длина каждого получающегося отрезка отвечает 10 или 1% содержания данного компонента в смеси.

Выражение составов трехкомпонентных систем по Розебому основано на том, что сумма отрезков, проведенных из какой-либо точки внутри треугольника параллельно его сторонам до пересечения с каждой из сторон, равна длине стороны треугольника. Координатная сетка образована тремя группами прямых, параллельных сторонам треугольника. Содержанию каждого компонента отвечает длина отрезка, проведенного к стороне, лежащей против вершины этого компонента. На рис. 10.1 эти отрезки нанесены пунктиром; длины отрезков oa,obіocсоответствуют содержаниям компонентов A, B, C.

Линии, параллельные одной из сторон треугольника, представляют геометрические места точек, соответствующих смесям с одинаковым содержанием одного из компонентов. Например, линия mnотвечает смесям, в которых содержание компонента B составляет 65%.

Линии, проведенные из вершин треугольника до пересечения с противолежащей стороной, являются геометрическими местами точек, соответствующих ряду систем, в которых соотношение между содержанием двух компонентов остается постоянным. Так, например, линия Bхотвечает ряду смесей, в которых процентное содержание A и C сохраняется равным 8:2.

К треугольной диаграмме, как и диаграмме бинарных систем, приложимо правило рычага. Если, например, точка ротвечает общему составу системы, а система распадается на две фазы составовkиl, то количество первой фазы относится к количеству второй как длины отрезковpl :pk.

Составы трехкомпонентных систем иногда изображают в прямоугольных координатах, что значительно упрощает расчеты количеств отдельных фаз. Этот способ чаще всего применяют для изображения состава растворов двух солей с общим ионом. Для построения прямоугольной диаграммы состав системы выражают не в мольных или массовых процентах, а числом молей или граммов каждой соли, приходящихся на 100 молей или 100 граммов воды (или другое постоянное количество). При этом на оси абсцисс откладывают содержание одной соли, а на оси ординат – содержание другой. Начало координат соответствует чистому растворителю.

Источник

Способы графического изображения фазовых диаграмм трехкомпонентных систем

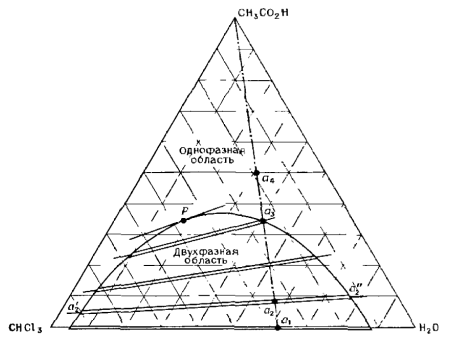
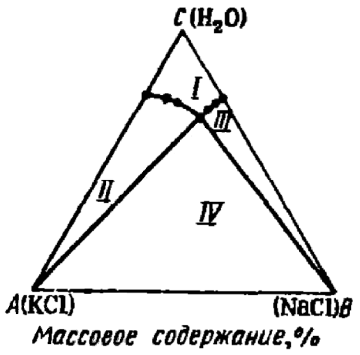
На третьем курсе на занятиях по физической химии мы изучали различные диаграммы состояния. Особо запомнились своим довольно необычным видом такие диаграммы при постоянных температуре и давлении для систем, состоящих из трёх веществ, так как изображались они в виде равностороннего треугольника (т. н. «треугольник Гиббса-Розебома»), где каждая его точка соответствовала смеси какого-либо определённого состава (рис. 1, 2), а концентрации выражались как доли компонентов.

Рис. 1. Трёхкомпонентная система уксусная кислота – хлороформ – вода при комнатной температуре [1, с. 338].

Рис. 2. Диаграмма растворимости KCl и NaCl в воде при 298 К [2, с. 485].

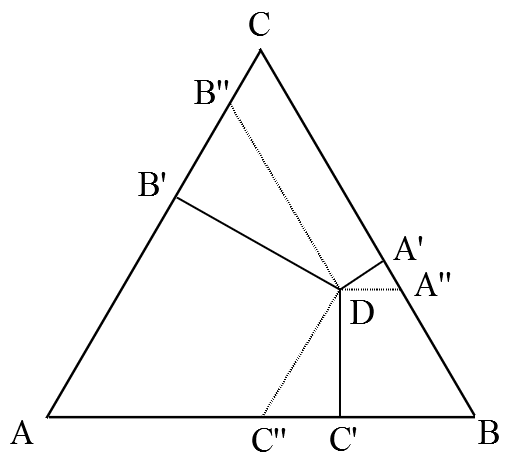
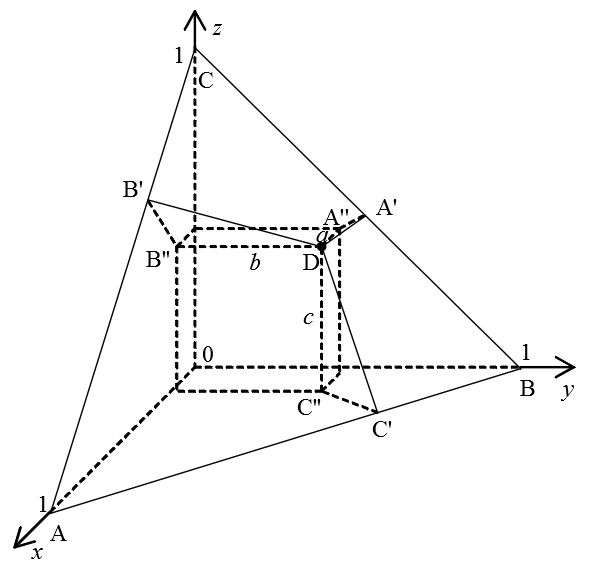
Также на лекциях нам рассказывали про два правила, по одному из которых каждой точке треугольника-диаграммы ставился в соответствие состав трёхкомпонентной смеси. Опишу кратко эти правила [3, с. 229] на примере системы из веществ A, B и C, мольные доли которых составляют x , y и z соответственно. Рассмотрим точку D внутри равностороннего треугольника △ABC (рис. 3). Какому соотношению x : y : z она соответствует?

Рис. 3. Определение состава смеси по правилам Гиббса и Розебома.

1) По правилу Гиббса высота треугольника принимается за единицу (или за 100%) и используется тот факт, что сумма длин перпендикуляров, опущенных из точки D на стороны треугольника равна его высоте. В этом случае концентрации (доли) компонентов пропорциональны длинам этих перпендикуляров:

x : y : z = DA’ : DB’ : DC’

2) По правилу Розебома за единицу (за 100%) принимается длина стороны треугольника, при этом из точки D проводятся отрезки, параллельные каждой из его сторон (на рис. 3 это DA», DB», DC»). Сумма их длин равна стороне треугольника и выполняется следующее соотношение:

x : y : z = DA» : DB» : DC»

или в иной записи

Легко видеть, что правила Гиббса и Розебома нисколько не противоречат друг другу:

x : y : z = DA’ : DB’ : DC’ = DA» : DB» : DC»

Это обусловлено тем, что △DA’A», △DB’B» и △DC’C» являются подобными (как треугольники с равными углами: ∠DA’A» = ∠DB’B» = ∠DC’C» = 90°; а ∠DA»A’ = ∠DB»B’ = ∠DC»C’ = 60°, поскольку DA» || AB, DB» || BC, DC» || AC).

Простого запоминания описанных правил вполне хватило для подготовки к сдаче экзамена, тем более дальнейшая жизнь сложилась так, что за все последующие годы с диаграммами состояния мне иметь дело особо-то и не доводилось. Тем не менее в те времена появилось ощущение, что что-то в этих правилах определения состава системы меня смущает и спустя год я понял, что же именно. Дело было в следующем. Очевидно, что доли компонентов системы связаны между собой соотношением

однако из такого равенства неизбежно следует, что для графического изображения множества точек, координаты которых удовлетворяют такому равенству, необходимо использовать трёхмерное пространство, потому что переменных в уравнении три, но при этом треугольник Гиббса-Розебома – это именно треугольник, то есть плоская (двумерная) фигура. Почему так? В итоге до меня дошла очень простая вещь: если переписать (3) как

то получается известное из аналитической геометрии «уравнение плоскости в отрезках», которое в общем виде записывается так:

где l , m и n – точки, в которых данная плоскость пересекает оси абсцисс, ординат и аппликат соответственно. Отсюда получается, что треугольник Гиббса-Розебома располагается именно в плоскости, описываемой уравнением (4). Можно сказать иначе: поскольку каждая из величин x , y , z принимает значения от 0 до 1 (потому что это доли компонентов в смеси), то треугольник Гиббса-Розебома является расположенным в первом октанте графиком функции

Из этого факта как раз и следует, что для построения диаграммы состояния трёхкомпонентной системы вполне достаточно плоского изображения. А ещё любопытно здесь другое. Взгляните на рис. 4 – на нём изображён треугольник Гиббса-Розебома в «трёхмерном» представлении.

Рис. 4. Треугольник Гиббса-Розебома, представлен­ный как график функции z = 1 – x – y .

В △ABC выбрана точка D, от которой к сторонам этого треугольника проведены перпендикуляры DA’, DB’, DC’. Сама точка D имеет координаты ( a , b , c ), численные значения которых являются концентрациями входящих в состав смеси компонентов. Вершины △ABC с точкой начала координат образуют тетраэдр и из симметрии данного геометрического тела следует, что двугранные углы, образованные плоскостью △ABC и координатными плоскостями, равны. При этом в соответствии с теоремой, обратной теореме о трёх перпендикулярах , получается, что A’A» ⊥ BC, B’B» ⊥ AC, C’C» ⊥ AB, следовательно ∠DA’A», ∠DB’B» и ∠DC’C» являются линейными углами соответствующих двугранных углов, и значит они равны между собой. Отсюда вытекает, что △DA’A», △DB’B» и △DC’C» – подобные, из чего напрямую получается соотношение для правила Гиббса, аналогичное (1):

В связи с этим мне в голову уже давно закралась следующая мысль: а может создатели диаграмм состояния, когда разрабатывали способы наглядного преставления характеристик трёхкомпонентых систем, руководствовались схожими соображениями – про уравнение плоскости «в отрезках», про получающиеся при этом подобные треугольники и т. д.? Не удивлюсь, если такое действительно было опубликовано тем же самым Дж.У. Гиббсом в своих научных работах, а теперь, спустя более века и став классикой, успело подзабыться. В учебниках по физической химии, на которые я выше ссылался, и в ряде других [5, с. 422; ; 7, с. 401], сведений, подтверждающих приведённые догадки, нет – такую информацию нужно искать специально, но сначала необходимо суметь заставить себя заняться подобными поисками.

Кстати, схожая ситуация наблюдается и в отношении «правила креста» – очень легко отыскать литературу и сайты, где подробно рассказывается как решать задачи на смешение растворов с использованием этого правила, а вот материала, в котором описано откуда именно это правило берётся (то есть его математическое обоснование), мне обнаружить не удалось – пришлось восполнять этот пробел самостоятельно написанием соответствующей заметки.

1. Эткинс П. Физическая химия. Том 1. М.: Мир, 1980. – 586 с.
2. Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика. Учеб. для вузов / Под ред. К.С. Краснова – 3-е изд., испр. – М.: Высшая школа, 2001. – 512 с.
3. Карякин Н.В. Основы химической термодинамики: Учеб. пособие для вузов. Нижний Новгород: Издательство ННГУ им. Н.И. Лобачевского; М.: Издательский центр «Академия», 2003. – 464 с.
4. Геометрия: Учеб. для 10-11 кл. сред. шк. / Л.С. Аганасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1992. – 207 с.
5. Курс физической химии, том 1 / Под ред. Я.И. Герасимова. М.: Химия. 1964. – 624 с.
6. Карапетьянц М.Х. Химическая термодинамика: Учебное пособие. Изд. 4-е. М.: Книжный дом «ЛИБРОКОМ», 2013. – 584 с.
7. Киреев В.А. Курс физической химии. Изд. 3-е, перераб. и доп. М.: Химия, 1976. – 775 с.

Источник

Способы изображения состава трёхкомпонентных систем

Способы изображения состава бинарных систем.

Схема фазовых превращений двух- и многокомпонентных систем.

С появлением в системе двух и более компонентов в закономерностях фазовых изменений возникают свои особенности.

В уравнениях состояния двухкомпонентных систем число независимых переменных равно четырём: T, p, c₁, c₂. Таким образом, для построения полной диаграммы состояния необходимо располагать системой координат четырёх измерений. В этих координатах диаграмма должна представлять собой совокупность поверхностей, расположенным некоторым образом в четырёхмерном пространстве. Подобное построение невозможно, и это вынуждает прибегать к некоторым упрощениям, вернее, к использованию таких переменных, описывающих состояние системы, которые позволяют сделать необходимое упрощение.

С этой целью вместо переменных T, p, c₁, c₂ переходим к переменным T, p, мольному объёму V и мольной доле первого компонента x₁. Мольная доля второго компонента x₂ при этом уже не может быть величиной независимой, она равна 1-x₁.

Поскольку по всем трём осям трёхмерной диаграммы откладываются значения независимых переменных, каждая точка внутри этой диаграммы имеет физический смысл. Всё пространство объёмной диаграммы разделено поверхностями раздела на области, охватывающие такие сочетания значений T, p, x₁, при которых могут существовать отдельные фазы.

В практической повседневной работе пользуются ещё более упрощёнными диаграммами, а именно сечениями объёмной диаграммы плоскостями, отвечающими постоянному давлению или постоянной температуре. Поскольку нам в наших исследованиях приходится часто иметь дело с превращениями, протекающими при постоянном давлении или при постоянной температуре, подобные сечения вполне удовлетворяют многие потребности теории и практики.

Состав трёхкомпонентной системы удобно изображать, пользуясь концентрационным треугольником. Вершины равностороннего треугольника отвечают содержанию в системе 100 % каждого из компонентов А, В и С. Стороны треугольника позволяют описать составы двухкомпонентных систем А+В, В+С, С+А.

Точки, лежащие внутри треугольника, описывают составы трёхкомпонентных систем.

Метод определения состава, предложенный Гиббсом, основан на том, что сумма перпендикуляров, опущенных из любой точки внутри равностороннего треугольника на каждую из сторон, равна высоте треугольника.

Фазовое поведение трёхкомпонентных углеводородных смесей в ряде случаев может быть корректно смоделировано посредством представления этих смесей как псевдобинарные. Многокомпонентная смесь приводится к псевдобинарной специальным образом. Трёхкомпонентная смесь получается смешением одного чистого компонента и бинарной смеси двух других компонентов. В случае четырёхкомпонентной смеси смешиваются бинарные смеси.

Указанный метод, применимый к любой многокомпонентной системе, для наглядности изложения применим к трёхкомпонентным смесям. Условие представления трёхкомпонентной смеси как псевдобинарная, вытекает из метрических свойств концентрационного треугольника (рис.1). Точки, отвечающие составу рассматриваемого раствора и образующих его смесей (А, В, С), должны лежать на одной прямой линии: секущей концентрационного треугольника, выходящей из вершины, соответствующей чистому наиболее высококипящему компоненту (К3 на рис.1).

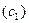
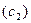
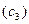
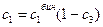
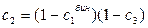
При изменении состава тройного раствора по секущей молярные доли и компонентов К1 и К2 зависят от молярной доли компонента К3 следующим образом:

и , (1)

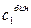
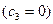
где — молярная доля компонента К1 в исходной бинарной смеси .

Условия фазового равновесия в трёхкомпонентной системе могут быть описаны, как показано в [4], уравнениями по форме аналогичными уравнениям, выражающим условия фазового равновесия в бинарных смесях. Это заключение может быть распространено на системы с числом компонентов больше трёх, поскольку любой многокомпонентный раствор может рассматриваться как продукт смешения одного чистого компонента и сложного «компонента», представляющего собой определённую смесь всех остальных компонентов рассматриваемой системы.

Рис. 1. Концентрационный треугольник для выражения состава трёхкомпонентной системы

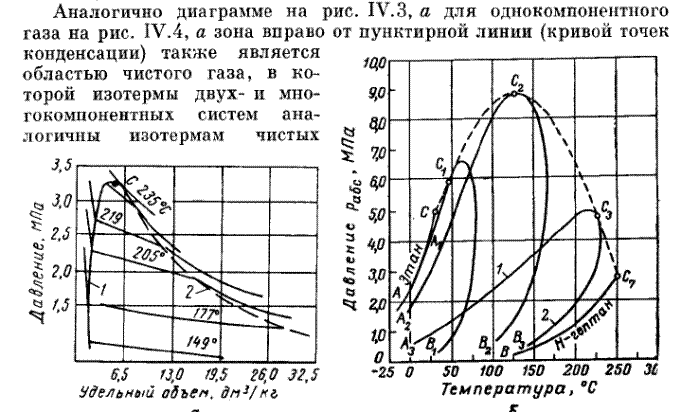
На рис. 4, а приведена зависимость «объем — давление» для смеси пентана и гептана с массовой концентрацией последнего 52,4%.

Рис. 4. Диаграммы фазового состояния двухкомпонентных систем.

а — зависимость «давление — удельный объем» для смеси н-пентана и н-гептана, содержащей 52,4% по массе н-гептана; б — диаграмма «давление — температура» для смесей этана с н-гептаном (точки C₁, С₂ и C₃ — критические точки смесей, содержащих соответственно 90,22, 50,25 и 9,8% по массе этана); 1 —линия точек начала парообразования; 2 —линия точек росы.

компонентов. Влево от кривой точек парообразования изотермы жидкой фазы круто возрастают с уменьшением объема и они также аналогичны изотермам области жидкости чистых компонентов. В двухфазной же области двух- и многокомпонентных систем имеются значительные изменения. В области двухфазного состояния чистых углеводородов изотермы характеризуются горизонтальными линиями, т. е. давление не изменялось до полной конденсации газа (рис. 3).

Для двух- и многокомпонентных систем, как это следует из рис. 4а, давление в процессе сжатия в двухфазной области не остается постоянным и для конденсации газа необходимо повышать его для полного превращения газовой фазы в жидкость. Поэтому давление точки парообразования (кипения) для двух- и многокомпонентной смеси выше точек конденсации. В соответствии с этим не одинаков и состав жидкой и газовой фаз в точках парообразования и конденсации. Вскоре после начала конденсации газа состав последнего еще близок к составу всей системы. Точно так же вблизи точки парообразования состав жидкой фазы близок к составу исходной смеси. В двухфазной же области состав жидкой и газовой фаз отличен от состава исходной смеси и он непрерывно изменяется в соответствии с давлением и объемом системы.

Бинарные и многокомпонентные системы также имеют свои особенности и в области, лежащей вблизи критических давлений и температур. Критическая точка чистых веществ (или однокомпонентных систем) характеризуется самыми высокими давлениями и температурой, выше которых невозможно одновременно существование двух фаз — жидкой и газообразной. В бинарных и многокомпонентных системах критическая точка характеризуется лишь одинаково интенсивными свойствами газовых и жидких фаз. При этом в зоне пересечения кривых точек конденсации и парообразования образуется область, в которой могут существовать две фазы даже при температурах и давлениях, превышающих критические значения.

С появлением в системе второго компонента большие различия появляются также в диаграммах «давление — температура». Кривые точек начала кипения и точек росы не совпадают и образуют фазовую диаграмму, на вид которой, кроме температуры и давления влияет исходный состав смеси. Крайние левая и правая кривые на диаграмме (рис. 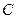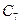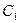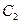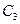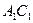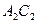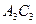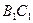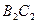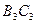4б) соответствуют давлениям насыщенного пара для чистых компонентов — этана и н-гептана с критическими точками и . Между ними расположены фазовые диаграммы смесей этана с н-гептаном с массовой концентрацией этана 90, 22; 50, 25 и 9,8% с соответствующими критическими точками , и . Пунктирная линия представляет собой огибающую критических точек системы этан — н-гептан. Линии , и представляют собой линии точек начала кипения рассматриваемых смесей (выше и слева от них смесь находится в жидком состоянии), , и — линии точек росы соответствующих смесей. Ниже и справа от этих линий смесь находится в газообразном состоянии. Между линиями точек начала кипения и точек росы располагается двухфазная область. Из рис. 4, б видно, что с увеличением содержания н-гептана в системе критическая точка, располагающаяся слева от максимальных значений давления и температуры, при которых две фазы могут существовать в равновесии, сдвигается вправо от нее. Кривые же точек росы и начала кипения при этом приближаются к кривой давления насыщенного пара, преобладающего в смеси компонента — н-гептана. Аналогично изменяются также критические температуры и давления при изменении состава смеси.

Величина критической температуры различных смесей находится между критическими температурами компонентов. По имеющимся экспериментальным данным для ее вычисления можно использовать свойство аддитивности (расчетные значения критических температур при этом получаются более близкими к действительным при выражении состава в процентах по массе, а не в молярных).

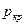
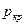
Критическое же давление смеси обычно выше, чем критическое давление чистых компонентов, кроме тех случаев, когда в смеси один из компонентов содержится в значительном количестве (т. е. правило аддитивности для вычисления смеси нельзя применять). Отклонение фактической величины от вычисленного критического давления по правилу аддитивности возрастает с увеличением разницы между молекулярными массами чистых компонентов. Наибольшее критическое давление обычно наблюдается у смеси с близким массовым содержанием обоих компонентов.

Как видно из рис. 4, б, размеры двухфазной области также зависят от состава смеси — они возрастают по мере того, как в составе смеси распределение между компонентами становится более равномерным.

Естественные углеводородные смеси отличаются большим разнообразием состава. Поэтому фазовые диаграммы нефтегазовых смесей, сохраняя принципиальные черты фазовых переходов двухкомпонентных систем, обладают еще своими в основном количественными особенностями, зависящими от состава нефти и газа.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник