МЕТОДЫ СЪЕМКИ ПОДРОБНОСТЕЙ МЕСТНОСТИ



Съемку характерных подробностей ситуации местности производят в зависимости от конкретных условий местности и имеющихся в наличии приборов одним из следующих способов: прямоугольных координат; полярным; прямых угловых засечек; линейных засечек; обхода; створов; на-земно-космическим.
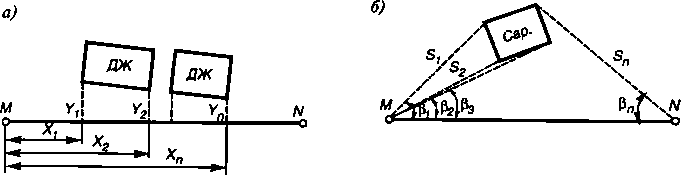
Рис. 15.1. Схема теодолитной съемки методом координат: а — прямоугольных; б — полярных
При съемках методом прямоугольных координат положение каждой ситуационной точки местности устанавливают по величинам абциссы X (расстоянием от ближайшей точки съемочного обоснования по стороне теодолитного хода или расстоянием от начала трассы) и ординатой У (расстоянием от соответствующей стороны теодолитного хода или от трассы) (рис. 15.1, а). Определение ординат У обычно производят с помощью зеркального эккера и рулетки.
Метод прямоугольных координат наиболее часто используют при съемке притрассовой полосы линейных сооружений в ходе разбивки пикетажа. Ширину съемки притрассовой полосы в масштабе 1:2000 принимают по 100 м в обе стороны от трассы, при этом в пределах ожидаемой полосы отвода съемку ведут инструментально, а далее глазомерно.
Теодолитную съемку методом полярных координат применяют преимущественно в открытой местности, при этом положение каждой ситуационной точки определяют горизонтальным углом Р, измеряемым от соответствующей стороны теодолитного хода, и расстоянием 5, измеряемым от соответствующей точки съемочного обоснования (рис. 15.1, б). Съемку характерных точек местности наиболее часто осуществляют оптическими теодолитами с измерением расстояний нитяным дальномером.
Съемка методом полярных координат оказывается особенно эффективной при использовании электронных тахеометров.
Метод прямых угловых засечек применяют главным образом в открытой местности, там, где не представляется возможным производить непосредственное измерение расстояний до интересуемых точек местности. Положение каждой снимаемой точки относительно соответствующей стороны теодолитного хода (базиса) определяют измерением двух горизонтальных углов $\ и р2> примыкающих к базису (рис. 15.2, а). В качестве базиса обычно служит одна из сторон съемочного обоснования или ее часть. Съемку методом прямых угловых засечек обычно ведут оптическими теодолитами и особенно часто используют при производстве
 |

Метод линейных засечек применяют, если условия местности позволяют легко и быстро производить линейные измерения до характерных ситуационных точек местности. Измерения производят лентами или рулетками от базисов, расположенных на сторонах съемочного обоснования. Положение каждой снимаемой точки местности определяют измерением двух горизонтальных расстояний $1 и 8г с разных концов базиса (рис. 15.2, б).
Метод обхода реализуют проложением теодолитного хода по контуру снимаемого объекта с привязкой этого хода к съемочному обоснованию. Углы рь Рг. Ри снимают при одном положении круга теодолита, а измерения длин сторон осуществляют землемерной лентой или рулеткой, нитяным дальномером или светодальномером электронного тахеометра (рис. 15.3, а).
Метод обхода используют, как правило, в закрытой местности для обозначения недоступных объектов значительной площади: болота, запретные зоны, территории хозяйственных объектов и т. д.
Суть метода створов состоит в том, что на прямой между двумя известными точками, размещенными на сторонах съемочного обоснования
°) о б)
 |
| N -о |
.с
■о—
Рис. 15.3. Схема теодолитной съемки методами: а — обхода; б — створов
(например М и Ы), с помощью одного из мерных приборов определяют положение характерных ситуационных точек местности (рис. 15.3, б).
Метод створов находит применение, главным образом, при изысканиях аэродромов, для установления ситуационных особенностей местности в ходе топографических съемок методом геометрического нивелирования по квадратам. При производстве изысканий других инженерных объектов метод створов применяют крайне редко.

Наземно-космический метод горизонтальной съемки состоит в том, что для получения плановых координат характерных ситуационных точек местности используют приемники систем спутниковой навигации «ОР8». Учитывая высокую стоимость приемников ОР8 высокого класса точности («геодезическою класса»), можно воспользоваться сравнительно недорогими приемниками среднего класса точности («класса ГИС»), но при использовании их в режиме работы с базовыми станциями — «дифференциальными ОР8 — ООР8».
Принцип горизонтальной съемки наземно-космическим методом в режиме «ООР8» состоит в получении координат ситуационных точек местности с геодезической точностью посредством корректирующих сигналов приемниками «ОР8» среднего класса от базовой станции «ЭОР8», установленной на точке местности с известными координатами (например, на пункте государственного геодезической сети). Обычно одна базовая станция обслуживает съемку приемниками «ОР8» в радиусе до 10 км.
Источник
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Горизонтальная съемка
Горизонтальная съемка местности в простейшем варианте выполняется с помощью теодолита и рулетки. Съемочное обоснование обычно создают проложением теодолитных ходов. Если участок съемки имеет вытянутую форму, то теодолитный ход прокладывают по его оси; при этом отдельные пункты съемочного обоснования можно определять из геодезических засечек. Если участок имеет овальную форму, то прокладывают замкнутый ход по его границе; внутри участка можно проложить диагональные ходы.
При горизонтальной съемке положение отдельных точек определяют относительно пунктов съемочного обоснования и линий, соединяющих их, применяя:
способ засечек ( угловых, линейных, комбинированных );
полярный способ;
способ перпендикуляров;
способ створов.
Широко также применяется способ обмеров зданий и сооружений и расстояний между ними с помощью рулетки.
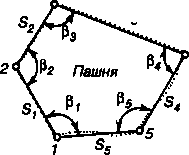
Способ засечек. При угловой засечке положение точки 1 определяют относительно двух пунктов съемочного обоснования А и В с помощью двух измеренных горизонтальных углов α1 и β1. Положение другой точки – точки 2 определяют, измеряя два других угла α2 и β2 (рис.7.3). Результаты измерений записывают в журнал.
При построении плана при точках А и В с помощью транспортира строят углы α1 и β1 и в пересечении линий получают изображение точки 1 на плане. Аналогично находят на плане положение точки 2.
Если расстояние до точки 1 не превышает длины рулетки, положение точки 1 определяют линейной засечкой, при которой измеряют расстояния А – 1 и В – 1 ; при построении плана из точки А проводят дугу радиусом, равным расстоянию А – 1 в масштабе плана, а из точки В – радиусом, равным расстоянию В – 1 в масштабе плана. Точка пересечения этих дуг является изображением точки 1 на плане.
Точность измерения горизонтальных углов при угловой засечке определяется точностью их построения на плане транспортиром,т.е. порядка 10′ – 15′. Допустимую ошибку измерения расстояний при линейной засечке рассчитывают по формуле:
где М – знаменатель масштаба съемки.
Полярный способ. Полярный способ съемки – это реализация полярной системы координат. Теодолит устанавливают на пункте съемочного обоснования А, принимая его за начало ( полюс ) местной полярной системы координат. Полярная ось совмещается с направлением на другой пункт съемочного обоснования В. Затем измеряют горизонтальный угол β1, образованный направлением АВ и направлением на снимаемую точку 1, и расстояние S1 от точки А до точки 1 (рис.7.4). При построении плана положение точки 1 получают, откладывая на стороне угла β1, построенного транспортиром, расстояние S1 в масштабе плана.
Рассчитаем среднюю квадратическую ошибку измерения углов и расстояний при полярном способе съемки, если ошибка положения точки 1 задана и равна Мp.
В полярной системе координат ошибка положение точки выражается формулой:
где mβ – ошибка измерения угла β; ms – ошибка измерения полярного расстояния.
По принципу равных влияний имеем:
m2s = ( S * mβ/

Пусть масштаб съемки 1:М=1:2 000, тогда Мp=0.5 мм * 2 000=1 м. При S=100 м вычисления по формулам (7.3) дают mβ=24′, ms =0.7м, ms/S = 1/150.
Способ перпендикуляров. Способ перпендикуляров является реализацией обычной прямоугольной системы координат. Пусть линия АВ – одна из сторон теодолитного хода. Примем ее за ось l, начало координат совместим с пунктом А; ось d расположим перпендикулярно линии АВ. Положение точки 1 определяется двумя перпендикулярами l1 и d1 (рис.7.5), длины которых измеряют мерной лентой или рулеткой.
Для построения прямого угла β можно применть теодолит или эккер; иногда угол β = 90 можно построить на глаз. Положение точки 1 на плане получают после выполнения трех операций: откладывания вдоль линии АВ длины перпендикуляра l1, построения угла β =90 c помощью транспортира, откладывания на стороне угла β длины второго перпендикуляра d1.
Съемка других точек и определение их положения на плане выполняются в таком же порядке.
Ошибка положения точки Мp в способе перпендикуляров складывается из ошибки измерения перпендикуляра l, ошибки построения (или измерения) угла β = 90 o и ошибки измерения перпендикуляра d:
М2p = m^2l + mβ ^2/
По принципу равных влияний полагаем:
m^2l = m β^2/ 
При Мp = 0.5 мм на плане получим 
в масштабе плана при относительной ошибке его измерения:
md / d = 0.33 мм / 33 м = 1/110.
Для плана масштаба 1 : 2 000 расчетная длина перпендикуляра d получается 66 м, а для масштаба 1 : 500 – d = 16 м. В Инструкции эти величины заданы 60 м и 20 м соответственно.
Разумеется, при другом значении ошибки mβ допустимая длина перпендикуляра d будет другой. Например, строя угол β = 90 “на глаз” (mβ = 1) , получим d = 16 мм в масштабе плана.
При горизонтальной съемке результаты измерений углов и линий записывают в журнал. Кроме того, прямо в поле составляют схематический чертеж местности – абрис, на котором показывают все пункты съемочного обоснования, контуры, ситуацию местности, записывают результаты измерений, делают пояснительные записи.
По материалам съемки составляют и вычерчивают план участка.
Теория и устройство эккера. Эккер – прибор для построения на местности прямых углов. Эккеры бывают зеркальные и призменные. Зеркальный эккер состоит из трехгранной коробки, одна из боковых граней которой открыта (рис.7.6). К двум другим граням с внутренней стороны прикреплены зеркала. Над зеркалами вырезаны окошки. Внизу эккера имеется крючок для отвеса.
Пусть эккер установлен на линии АВ (рис.7.7). Луч от вехи А попадает в зеркало Z1, отражается от него, падает на зеркало Z2, отражается от него и попадает в глаз наблюдателя, составляя со своим первоначальным направлением угол ε. Теория эккера заключается в выводе формулы ε = ε (γ), где γ – угол между зеркалами.
Обозначим : α – угол падения и угол отражения на зеркале Z1, β – угол падения и угол отражения на зеркале Z2.
Угол ε является внешним углом треугольника СЕК, поэтому:
ε = 2 * α + 2 * β = 2 * (α + β ). (7.6)
В треугольнике ЕОК:
Для того, чтобы луч составлял со своим прежним направлением угол β = 90, нужно, чтобы угол между зеркалами был равен 45.
Глаз видит изображение вехи А в зеркале Z2 в направлении СЕ, перпендикулярном направлению АВ, а в окошко над зеркалом видно веху D, которую помощник переставляет по команде наблюдателя. Как только веха D будет находиться на линии CE, ее закрепляют.
Если вехи закреплены, то с помощью эккера можно найти на линии АВ точку С, чтобы линия DC была перпендикулярна АВ; другими словами, можно найти основание перпендикуляра, опущенного из точки D на линию АВ. Взяв в руки эккер, перемещаются по линии АВ, пока изображение вехи А в зеркале Z2 не совпадает с направлением CD. Затем при помощи отвеса намечают на земле точку С.
Поверка эккера. Угол между зеркалами должен быть равен 45. Стоя в точке С, строят прямой угол, наблюдая веху А, закрепляют прямой угол первой вехой. Затем, стоя по-прежнему в точке С, строят прямой угол, наблюдая веху В, закрепляют прямой угол второй вехой. Если вехи оказались рядом, условие эккера выполняется. В противном случае намечают среднее положение, ставят веху в эту точку и юстировочными винтами зеркал изменяют угол между зеркалами до тех пор, пока изображение вехи А или В не совпадет с направлением CD. После этого поверку повторяют. Эккер считается исправным, если угол γ отличается от 45 не больше, чем на 2.5′, тогда ошибка построения угла β = 90 будет не больше 5′.
Источник