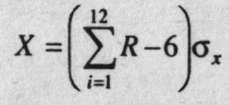Способы генерации случайных величин

Генерирование случайных величин

В большинстве случаев при имитационном моделировании ис­пользуют программные методы получения случайных чисел. Такие числа уже нельзя назвать «случайными», но они обладают многими статистическими свойствами строго случайных чисел. В литературе они получили название «псевдослучайных» чисел. В настоящее вре­мя большинство программ, генерирующих псевдослучайные числа, используют конгруэнтную процедуру, при которой каждое после­дующее число хм получается из предыдущего x_i. В основе конгру­энтных процедур генерирования псевдослучайных чисел лежит ма­тематическое понятие сравнения (congruence). Целые числа а и b считаются сравнимыми по модулю т, если эти числа дают одинако­вые остатки при делении на m (или, что то же самое, разность этих чисел делится на m без остатка). Математически процедуру сравне­ния записывают следующим образом: а =b(mod m) и читают «а, сравнимое с b по модулю m».

Искомая последовательность псевдослучайных чисел получается из соотношения: x_i+1≡ (ax_i+b)(mod m).

Из этого выражения следует, что количество различных псевдо­случайных чисел не может быть больше т. После генерации т чисел последующие числа начинают повторяться. При неудачном выборе величин а и b период может быть меньше т. Существуют теоретиче­ские предпосылки, позволяющие осуществить выбор чисел a, b и т. В частном случае b= 0, т.е.

X_i+1 = ах_i(mod m). Такой генератор назы­вают мультипликативным, и он дает достаточно хорошие результаты (полученные числа имеют хорошие статистические характеристики).

Количество различных псевдослучайных чисел зависит от разрядно­сти процессора, так как обычно модуль т принимают равным 2 k -1, где k — разрядность процессора.

Для удобства пользования псевдослучайными числами во всех ЭВМ имеется программа, дающая равномерное распределение в пре­делах 1 0 или х отсутст­вует, то генерируется очередное случайное число, но при повторном запуске последовательность повторяется.

В других языках программирования существуют аналогичные правила и операторы.

Если необходимы случайные числа с другими распределениями вероятностей, то после обращения к генератору, дающему случайные числа R в интервале (0,1), используют простые преобразования [3].

Из теории вероятностей известно, что равномерное распределение в интервале (А, В) получается преобразованием X=A+(B-A)*R. Математическое ожидание в этом случае будет

ЕХ =(B+A)/2, а дисперсия VX=(B-A) 2 /2.

Для получения нормального распределения с нулевым средним производится суммирование 12 случайных чисел R. Из суммы вычи­тается 6, а результат умножается на величину заданного среднеквадратического значения, так как дисперсия суммы равна единице,

Если среднее значение отличается от нуля, то к этому выражению добавляется величина, равная среднему значению.

Для получения экспоненциального распределения Р(х)=αe -αx , α > 0, х ≥ 0, производится операция х = -(l/α)log(R). При этом мате­матическое ожидание ЕХ=1/α и дисперсия VX = 1/α 2 = ЕХ 2 .

Источник

Методы генерация случайных чисел с равномерным законом распределения. Часть 1

Промышленность не стоит на месте. Еще в 1990 году псевдослучайные числа, длинной в целых 40 бит, сгенерированные на ЭВМ можно было угадать за несколько часов [1]. На сегодняшний же день, качественные характеристики псевдослучайных величин на ЭВМ поражает даже опытных математиков. Во многих областях применения алгоритмов генераций всевдослучайных чисел существует ряд ограничений, связанных с тем или иным недостатком методов их генерации. Совершенствованию существующих методов способствует высокий интерес к теме, который повышается с ростом числа публикаций. Пусть эта статья станет моим вкладом в развитие методов моделирования и генерации случайных процессов, так важных для моих исследований и разработок.

Предыстория

Краткий экскурс в историю методов генерации случайных чисел показывает, что в погоне за стохастичностью разработчики готовы были идти на крайние меры. Так в 1996 году был изобретен и запущен источник случайных чисел под названием Lavarand. Метод генерации чисел был сведен к обработке фотографии декоративного светильника – лавовой лампы, которая непрерывно меняла свой облик непредсказуемым образом [2]. Также стоит упомянуть и о первых генераторах случайных величин на обычных ЭВМ. Разработала их фирма Intel в 1999 году, и назывался данный компонент Firmware Hub. Метод генерации заключался в регистрации теплового шума резисторов с последующим усилением и использованием в качестве управляющего сигнала осциллятора, регулярно меняющего своё значением между “0” и “1” [3].Такая система работала непрерывно, вне зависимости от нужды пользователя в использовании системы генерации случайных чисел.
Главная проблема генерации истинно случайных чисел остается обязательное наличие аналоговой составляющей, так как качественные характеристики цифровых методов генерации псевдослучайных чисел не удовлетворяют многим стандартам National Institute of Standards and Technology, а на практике абсолютно не годятся для решения многих задач прикладного характера, например криптографии.

Рис.1 Схема генератора случайных чисел.

В апреле 2012 года в продажу поступили первые процессоры с микроархитектурой под кодовым названием “Ivy Bridge”. Особенностью этой архитектуры стало наличие генератора, позволяющего использовать аналоговые тепловые шумы напрямую для генерации случайных чисел [4]. На рис.1 представлена схема такого генератора. На первый взгляд она слишком идеализирована, ведь равновероятного появления “0” или “1” можно добиться только при абсолютной идентичности инверторов, чего на практике добиться невозможно. Поэтому неравномерность генерируемых чисел требуется компенсировать, что и делается в постобработке.

Генерация случайных чисел с равномерным законом распределения

Пожалуй, самым важными и незаменимыми методами моделирования случайных процессов, являются методы генерации равновероятных случайных величин, так как большая часть алгоритмов моделирования случайных процессов с произвольным законом распределения базируются именно на них [5].
Самыми популярными способами получения равномерно распределенных случайных величин являются:
• Таблицы случайных чисел
• Физические генераторы случайных чисел (такие как Firmware Hub или генератор случайных чисел в “ Ivy Bridge ”)
• С помощью цифровых генераторов или датчиков, с использованием формул.
Надо сказать, что в последнем пункте результатом генерации являются псевдослучайные числа. Как бы ни парадоксально звучало следующее утверждение, но главным недостатком таких чисел – это то, что в большинстве случаев их нетрудно предсказать, а в некоторых алгоритмах генерации их последовательность ещё и имеет свойство периодически повторятся. В некоторых прикладных задачах это недопустимо, но, несмотря на это, именно эти способы генерации случайных величин с равномерным законом распределения получили наибольшее распространение, ввиду простоты их реализации на ЦЭВМ.
Среди них наиболее популярными считают:
• Конгруэнтные методы.
• Методы, основанные на использовании регистра сдвига с линейной обратной связью (LFSR).
Линейный конгруэнтный метод по сей день используется для генерации случайных чисел в самых популярных средах программирования, таких как MSVS [6], MSVB [7], Java [6], Borland C/C++ [6], GCC [8] и других. Распространенность этого метода говорит о его эффективности.
Суть методов этого класса заключается в вычислении последовательности случайных чисел Y(n):
Y(n+1) = (x*Y(n) + c) % m,
где m – количество значений из которых формируется последовательность (m ≥ 2), % — остаток от деления, x – множитель (0 ≤ x

Источник

Подробно о генераторах случайных и псевдослучайных чисел

Введение

Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:

• Генераторы сессий (PHPSESSID)
• Генерация текста для капчи
• Шифрование
• Генерация соли для хранения паролей в необратимом виде
• Генератор паролей
• Порядок раздачи карт в интернет казино

Как отличить случайную последовательность чисел от неслучайной?

Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.

Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

• Предсказуемая зависимость между числами.
• Предсказуемое начальное значение генератора.
• Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.

Линейный конгруэнтный ГПСЧ (LCPRNG)

Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.

Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.

Предсказание результатов линейно-конгруэнтного метода

Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.

Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.

Взлом встроенного генератора случайных чисел в Java

Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы

Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)

Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).

Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:

до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так

Вывод данной программы будет примерно таким:

Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.

И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы успешно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.

Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так

Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.

Задание распределения для генератора псевдослучайных чисел

Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.

Треугольное распределение

Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так

Экспоненциальное распределение

Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

Источник