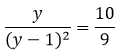Способы формирования теоретического мышления

РАЗВИТИЕ ТЕОРЕТИЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ 1–4-Х КЛАССОВ

Семина М.А., педагог-психолог МОУ «Средняя общеобразовательная школа № 2 с углубленным изучением английского языка»

Возникновение и развитие теоретического мышления является одним из первых и важнейших результатов развивающего обучения.

Своим содержанием, методами, формами организации развивающее обучение ориентированно на закономерности развития ребенка. В процессе развивающего обучения качественно изменяются, перестраиваются все сферы личности. А начинается эта перестройка с интеллектуальной сферы, прежде всего, с мышления.

Мышление нацеливается на раскрытие закономерностей происхождения и развития предметов.

Теоретическое мышление — развернутый в пространстве и времени процесс воспроизводства законов и принципов объективного существования предметов, поиск и раскрытие условий их происхождения. Это — обобщенный способ действия.

Теоретическое мышление включает в себя следующие компоненты: содержательный анализ, планирование, рефлексию.

Эти мыслительные действия, ориентированы на существенные и всеобщие особенности предметов.

Содержательный анализ направлен на поиск и выделение в целостном предмете основного и генетически исходного отношения.

Содержательное планирование заключается в поиске и построении системы потенциально возможных действий, соответствующих главным условиям задачи.

Содержательная рефлексия связана с поиском и рассмотрением
человеком существенных оснований собственных действий.

Все эти мыслительные действия взаимосвязаны. Планирование тесно связано с анализом и рефлексией, а анализ опирается на рефлексию. Их выполнение позволяет строить содержательные абстракции и обобщения.

Возникновение и развитие содержательных мыслительных действий связано с тем, что ребенок в процессе обучения сталкивается с принципиально новым для него типом знания — научным понятием. За каждым понятием скрыто особое действие или система таких действий, без выявления которого нельзя раскрыть механизм возникновения и функционирования данного понятия.

Теоретические знания являются основой развивающего обучения. Их усвоение происходит на основе понимания существенных связей между явлениями, которые ребенок устанавливает сам в специально организованной поисковой деятельности.

Формирование научно-теоретических понятий происходит посредством выполнения учащимися учебной деятельности. В младшем школьном возрасте учебная деятельность является основной и ведущей среди других видов деятельности. В нее входят следующие компоненты: учебно-познавательный интерес, целепологание (постановка и осознание познавательной цели), учебные действия, действие контроля, оценки.

Сохранение данной структуры на уроке и целенаправленное формирование каждого из компонентов определяет развитие теоретического мышления.

У детей, приходящих в 1 класс, целостной структуры учебной деятельности еще нет. В благоприятных условиях она развивается в течение нескольких лет школьной жизни, особенно интенсивно в начальных классах.

Чтобы у учащихся развивалась полноценная учебная деятельность и теоретическое мышление, они должны систематически решать учебные задачи. Главная особенность учебной задачи состоит в том, что при ее решении ребенок ищет и находит общий способ подхода ко многим частным задачам определенного класса, которые в дальнейшем не представляют для него особых трудностей.

Учебная задача решается посредством системы учебных действий (принятие учебной задачи, преобразование ситуации, моделирование, контроль, оценка процесса решения учебной задачи). Отдельные учебные действия связаны с рефлексией, анализом, планированием содержательного характера. Контроль основывается на содержательной рефлексии. Осуществление действия преобразования условий учебной задачи и моделирования связано с содержательным анализом предметного материала. Выполнение учебного действия, направленного на построение системы частных задач на основе общего способа их решения, предполагает содержательное планирование этого действия.

Для более эффективного развития мыслительных действий целесообразно использовать на уроках следующие задания и приемы.

Для развития содержательного анализа можно применять:

задачи с недостающими или избыточными данными — как в условии, так и в требовании задачи (для привлечения внимания детей к наличию в этих задачах разного рода данных полезно организовать коллективное обсуждение их условий и требований);
самостоятельное придумывание детьми задач с недостающими и избыточными данными, чтобы учащимся стала понятна необходимость тех или иных данных для построения проблемной ситуации;
превращение детьми обычных задач в задачи с недостающими и избыточными данными и наоборот (это способствует развитию умения детально и последовательно разбираться в материале разных задач);
исследование в классе изучаемых правил (способы получения правила, возможные следствия, особенности применения в разных условиях, связь с другими правилами).

Для развития содержательной рефлексии большое значение имеют обращения детей в процессе учебной работы к собственным действиям. Следует использовать разные виды такого обращения, а именно:

отчет о ходе уже проведенного решения задачи (это способствует, с одной стороны, развитию у детей умения планировать решение, а с другой — умению соотносить способ решения задачи с характерными особенностями ее типа);
предварительное обсуждение разных способов решения, когда эти способы сопоставляются по общности (это поможет детям научиться контролировать основание своих действий и оценивать их правильность);
рассмотрение действий с точки зрения особенностей результата, к которому они привели (это создает необходимые условия для того, чтобы обеспечить объективную оценку этих действий);
выяснение, к одному или разным типам принадлежат решаемые задачи, сходны или различны способы их решения, по каким особенностям совпадают или не совпадают их условия;
составление задач по предлагаемому образцу (например, придумать наиболее непохожую на образец, но родственную ему задачу, а также наиболее похожую, но решаемую на основе другого принципа).

Для развития внутреннего планирования:

целесообразно ставить детей в ситуацию, где необходимо объяснять, рассказывать способ решения задачи после ее практического решения (это лучше всего проводить в форме парной работы);
можно использовать устные задания:
1. решение легких задач с постепенным увеличением количества данных в условиях и требуемых действий для решения;
2. придумывание задач по данным условиям или требованию, а также задач, где известны лишь общие характеристики данных («Придумайте задачу, где известно одно слагаемое и сумма, а второе слагаемое неизвестно» или «Придумайте задачу, где два слагаемых неизвестны, но известны их сумма и разность»);
3. задания, опирающиеся на знания разрядности числа («Какое число будет, если в числе 427 число десятков увеличить на 4, а число единиц уменьшить на 2?»);
4. ступенчатый устный счет как в прямом, так и в обратном порядке;
5. задания на мысленное преобразование слов («Какое слово получится, если в слове «взгляд» убрать четыре буквы?»);
6. мысленное чтение слов наоборот;
7. мысленное преобразование фигур из палочек.

Такая работа предполагает разные способы взаимодействия детей между собой и учителем (диалог, дискуссия) и разные формы организации совместных действий.

Развивающее обучение специально рассчитано на формирование теоретического мышления, поэтому его наличие или отсутствие у учащихся – показатель того, достигнута ли одна из главных целей обучения.

Процесс развития теоретического мышления развернут во времени, и наиболее четкие его итоги могут быть зафиксированы к концу начальной школы. Но для эффективного развития мышления важно видеть каждого ученика и управлять развитием каждого из них. В течение всего периода обучения необходимо изучать особенности и уровень развития каждого ученика и класса в целом.

Для исследования теоретического мышления целесообразно использовать методики Л. И. Аршавиной, В. В. Давыдова и А. З. Зака. На основе особенностей решения детьми диагностических задач (в предметно-действенной и наглядно-образной форме) выявляется их уровень развития анализа, планирования и рефлексии.

Каждому возрасту соответствуют задачи своего уровня сложности.

По результатам диагностики можно констатировать, что мышление учеников (из одного класса) может находиться на разных стадиях своего развития.

Обучение создает все необходимые предпосылки и условия для развития теоретического мышления, но реализует их каждый ученик в меру своих возможностей. Развитие — процесс индивидуальный, поэтому его результаты не могут и не должны быть одинаковы у разных учеников. Главное, чтобы у каждого из них наблюдалась положительная динамика в развитии теоретического мышления. К четвертому классу большинство учащихся должны овладеть теоретическим способом решения задач.

Развитое теоретическое мышление позволяет осуществлять разумный выбор целей, средств, способов их достижения на основе понимания реальной ситуации, учета объективных условий и своих возможностей, критической оценки собственной деятельности и ее результатов.

Развивающее обучение задает такое направление интеллектуальному развитию, которое, в конечном счете, позволяет каждому стать подлинным субъектом сначала учения, а потом и всей своей жизни в целом.

Источник

LiveInternetLiveInternet

—Рубрики

Методические статьи (44)
Развивающее обучение (16)
Арифметика (7)
Алгебра (4)
Задачи на клетчатой бумаге (4)
Проценты (2)
Тригонометрия (1)
Мои инструменты (29)
Kandidat CMS (4)
Интернет (4)
Skype (3)
Online доски (2)
Youtube (2)
Электронная почта (2)
Фотошоп (2)
Решения тестов ЕНТ (14)
Уроки решения тестов ЕНТ (5)
Курс HTML5 и CSS3. II. Программы и настройки (4)
Курс HTML5 и CSS3. I. Введение (4)
Верстка сайта (4)
Бытовые наблюдения (3)
Функциональные уравнения (3)
Мои Интернет-проекты (3)
Рецензии (3)
Теория вероятностей (2)
Задания типа В10 (2)
Метод координат в задачах ЕГЭ (2)
Комбинаторика (1)
PHP (1)
КУРС HTML5 И CSS3. III. ТЕКСТ (0)
Решения задач (30)
Решения тестов ЕГЭ (31)
Задание типа В3 (2)
Старые записи о Интернет-проектах (4)

—Метки

—Поиск по дневнику

—Подписка по e-mail

—Статистика

Формирование теоретического мышления. Часть I

Суббота, 27 Сентября 2014 г. 12:33 + в цитатник

Пример формирования эмпирического мышления

Эмпирическое (опытное) мышление и познание представляет собой деятельность, в основе которой преобладает живое, непосредственное созерцание объекта.

Оно прежде всего сохраняет свою связь с восприятием. В ходе эмпирического мышления познаваемый объект отражается со стороны его внешних связей и свойств. В процессе познания познающий ориентируется на внешние условия существования объекта и на то содержание в нем, которое прямо доступно восприятию и наблюдению.

Результатом эмпирического мышления выступает знание непосредственного в действительности. В таком знании отражаются внешние сходные черты познаваемых объектов, но не его внутренняя сущность скрытая от внешнего созерцания.

Рассмотрим пример из обычной практики преподавания математики в средней общеобразовательной школе.

Решить уравнение

Эта задача кочует из одного методического пособия в другое. В прекрасном сборнике задач [1] предлагается такое решение.

Поделим числитель и знаменатель дроби, расположенной в левой части уравнения на х 2 , конечно, предварительно проверив число 0 на роль корня уравнения. После выполнения этой операции получим

Введем теперь обозначение х + 1/x = y, тогда наше последнее уравнение примет вид

10y 2 — 20y +10 = 9y, 10y 2 — 29y +10 = 0, D = 29 2 — 4 ⋅ 10 ⋅ 10 = 841 — 400 = 441 = 21 2 , y₁ = 0,8; y₂ = 2,5.

Читайте также: Кто придумал способ сохранения продуктов
Если y₁ = 0,8; х + 1/x =2/5; 5x 2 — 2x + 5 = 0. Это уравнение не имеет действительных корней.

Если y₂ = 2,5; х + 1/x =5/2; 2x 2 — 5x + 2 = 0; D = 25 — 4 ⋅ 2 ⋅ 2 = 3₂, x₁ =1/2; x₂ = 2.

Ответ: 1/2; 2.

Это типичный пример формирования эмпирического мышления учащихся, т . к. практика преподавания математики в современной школе предполагает после такого решения этого уравнения рассмотренным выше способом решение еще нескольких таких же аналогичных уравнений для того, чтобы учащиеся прочно овладели соответствующими навыками. Это и называют в современной школе закреплением.

Ни в пособии [1], ни в других пособиях, содержащих рассмотренное выше уравнение (или аналогичное) не проводится анализа решения.

Действительно, почему надо делить числитель и знаменатель дроби из левой части данного уравнения на х 2 . Это что новый метод? А может ничего нового здесь нет? А как рассмотренный прием (деления на х 2 ) согласуется с ранее приобретенными знаниями учащихся? Может быть мы уже применяли этот способ?

Все эти вопросы остаются без ответа. Нет даже попытки авторами методических пособий сформулировать эти вопросы. Типичный признак эмпирического преподавания математики: запомни, повтори, примени много много раз. Так и здесь.

В терминах классической методики преподавания математика здесь мы наблюдаем нарушение принципа научности. Действительно, НАУКА — это сфера человеческой деятельности, функция которой — выработка и теоретическая систематизация объективных знаний о действительности. Поэтому не ясно к какой системе знаний относятся метод решения этого уравнения.

Наука охватывает не только деятельность по получению нового знания, но и результаты этой деятельности — систему научных знаний, которая лежит в основе научной картины мира. Поэтому любые новые знания должны находиться в определенной связи с ранее полученной информацией или относится к новому разделу науки.

Другими словами, наше уравнение и его методы решения должны входить в систему знаний об уравнениях вообще и в систему знаний о некоторых, ранее изученных типах уравнений, так как только в этом случае образуется совокупность элементов, взаимосвязанных друг с другом и таким образом образующих определенную научно организованную целостность.

О том, что автор, предложивший этот метод решения нашего уравнения открыл нечто новое, еще неизвестное другим трудно себе представить. Наверное его «метод» — это нечто вырванное из контекста ранее известного.

Такой рецептурный подход преподавания математики изжил себя уже давно. Действительно, что будет, если так мы будем поступать со всеми уравнениями — предлагать для каждого из них «свой» рецепт решения. Выдержит ли память у учеников? Ведь она не безгранична! Сколько же нужно при этом тупо, механически запомнить и сколько нужно потратить времени на соответствующую тренировку чтобы как-то усвоить эти многочисленные доморощенные «методы».

Думаю, что поставленные мной вопросы говорят о том, что так преподавать математику сегодня нельзя. Нельзя даже описывать решения известных задач. В этом плане стоит поучиться у Л. Эйлера, который значительную часть своих статей посвящал описанию того как он получал решения научных вопросов и тому с какими известными задачами связано его решение.

В этой заметке я только критикую сложившуюся практику преподавания математики и не даю ответа на вопрос о том, как же надо преподавать математику, даже на примере решения на уроке рассмотренного выше уравнения. Это и будет целью моих следующих заметок, но уже закрытого типа.

Литература

Процитировано 3 раз
Понравилось: 1 пользователю

Источник