Растровая и векторная графика: это как?
Есть два вида картинок: в одной миллионы цветов и полный фотореализм; вторую можно увеличивать и уменьшать до бесконечности без потери качества. Вот как это всё работает.
👉 Как и большинство статей в журнале «Код», эта статья для начинающих. Юные Артемии, вам не сюда. Лучше порешайте наши задачки в паблике.
Растровая графика
Растр — это множество мелких точек, из которых может состоять изображение. В случае с компьютером растр — это пиксели, из которых состоит фотография.
Например, когда вы фотографируете на смартфон или цифровой фотоаппарат, вы получаете растровое изображение, которое состоит из множества отдельных точек. Если смотреть на экране телефона или компьютера, они не видны, но если сильно увеличить, то эти точки станут заметны.
Чем сильнее увеличим фотографию, тем больше видны пиксели
👉 У растровой графики есть два главных параметра: размер изображения и глубина цвета.
Размер изображения — это количество пикселей по горизонтали и вертикали. Чем больше размер, тем сильнее можно увеличивать картинку без потери качества. Например, возьмём одну и ту же фотографию, но у одной будет размер 100 на 200 пикселей, а у другой — 1000 на 2000 пикселей:
В одном и том же масштабе вторая картинка смотрится гораздо лучше, потому что в ней больше пикселей, которые передают больше деталей
Общее правило такое: чем больше пикселей на фотографии, тем больше мелких деталей можно на ней разглядеть. Именно поэтому производители камер и смартфонов постоянно увеличивают количество пикселей у себя в устройствах.
Глубина цвета. Представьте, что ваша камера в телефоне может различать только 16 цветов. В этом случае фотографии получались бы такими:
В целом понятно, что тут изображено, но выглядит странно
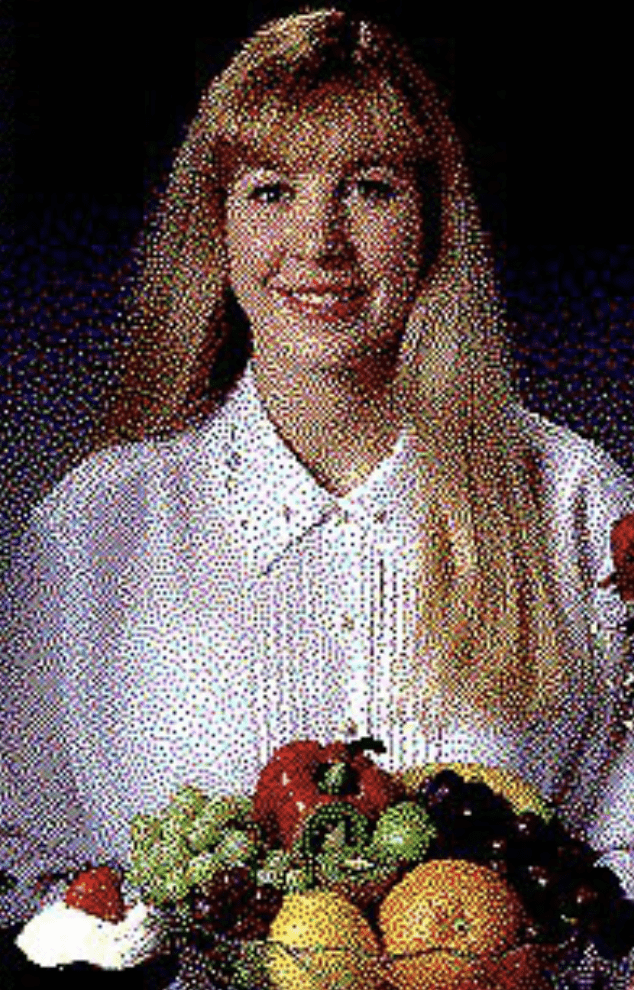
Это и есть глубина цвета — сколько разных оттенков присутствует на изображении. В нашем примере 16 цветов — это 4 бита, потому что 2 в 4 степени = 16. Сравните, как выглядит та же фотография с глубиной цвета 16 и 8 бит:
Чем больше глубина цвета, тем плавнее цветовые переходы на фото
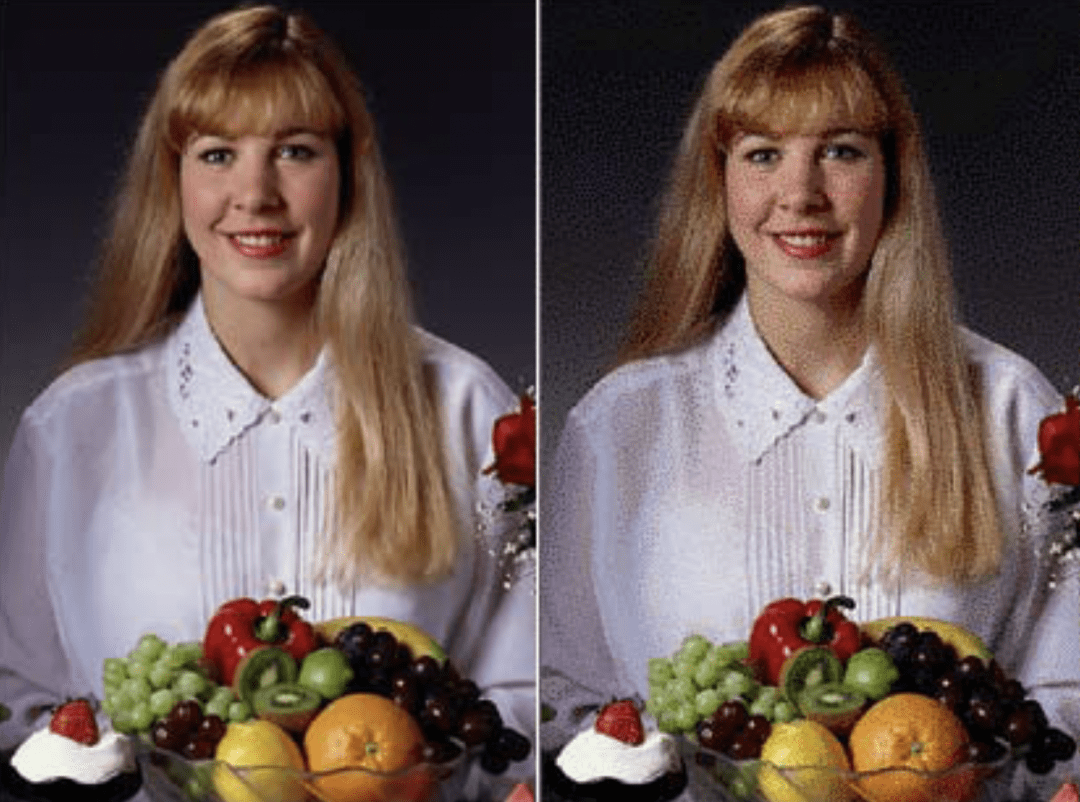
Главное применение растровой графики — фотографии и изображения с большой глубиной цвета и множеством деталей. Фотографии — это растр. Рисунки от руки — чаще всего растр. Если на изображении природа, люди, водичка или что угодно со множеством деталей, скорее всего, такое изображение будет растровым.
Компьютеры классно справляются с растровыми изображениями, потому что растр довольно прост в обработке. Компьютер ставит подряд нужное количество пикселей и красит их в нужные цвета. Операция простая, математика минимальная, просто нужно повторить её много раз. Компьютеры в этом сильны.
Векторная графика
В отличие от растровой графики, векторная состоит не из пикселей, а из математических формул. В такой графике каждое изображение нарисовано с помощью отдельных элементов:
- точек,
- эллипсов,
- прямоугольников,
- многоугольников,
- кривых любой сложности.
Чтобы это нарисовать, у каждого элемента есть свои параметры, например:
- координаты,
- цвет,
- размер,
- толщина линии,
- толщина контура,
- цвет контура,
- прозрачность,
- радиус кривизны и так далее.
Если компьютеру нужно нарисовать звёздное небо, мы можем дать ему такие команды:
- Создай пустой рисунок.
- Залей его градиентом сверху вниз от тёмно-синего к синему.
- Поставь точку <белая, размер 0,5, непрозрачность 100%>по координатам 10,8.
- Поставь точку <белая, размер 0,4, непрозрачность 100%>по координатам 14,9.
- Поставь точку <белая, размер 1,1, непрозрачность 80%>по координатам 19,31.
- … добавляем ещё 113 звёзд.
В итоге получим такой рисунок:
Избражение: wallpapersafari.com
Так как мы не привязаны к размеру изображения, то по этим формулам компьютер может нам отрисовать звёздное небо любого размера — от обоев на телефон до рекламного билборда 4 на 6 метров. При этом при увеличении потери качества не происходит — компьютер просто получает от нас финальный размер изображения и рисует всё в нужных пропорциях.
👉 Сила векторной графики — в возможности бесконечно увеличивать и уменьшать размер изображения без потери качества. При изменении размера компьютер сразу пересчитывает все формулы и отрисовывает картинку заново. Поэтому при увеличении векторной графики не появляются пиксели и размытие, даже если нам нужно увеличить одну звезду в 100 раз:
Минус векторной графики в том, что в ней очень сложно создать фотореалистичное изображение. Дело в том, что каждая деталь, каждый новый цвет и каждый цветовой переход — это новая формула. Чтобы построить фотореалистичную картинку, нужно очень много формул, которые будут сложно обсчитываться, и всё равно по деталям можно понять, что перед нами не фотография:
Каждый элемент на этой картинке задаётся своей формулой. Здесь много деталей, но всё равно видно, что это не фотография, а векторная иллюстрация 
То же самое изображение в кривых
Векторная графика чаще всего применяется там, где не нужна фотореалистичность — иконки, пиктограммы, рекламные материалы. Главная задача такого изображения — чтобы его можно было увеличить или уменьшить как угодно без потери качества.
‘ src=’https://thecode.media/wp-content/uploads/2021/01/image9.png’ alt=’Векторная графика’> Иконки — Сергей Чикин
Что дальше
Будем осваивать векторную графику в CSS. Заодно потренируемся наводить красоту на страницах и попрактикуемся в коде.
Источник
Способы формирования растровой графики
Известно, что на компьютере изображения представляются в цифровом виде. Цифровое – значит, описано посредством чисел. Это позволяет хранить, просматривать и обрабатывать изображение в графических редакторах.
Принцип формирования изображения в растровом и векторных редакторах кардинально отличаются друг от друга.
В растровом редакторе (Gimp, Adobe Photoshop, Paint) изображение разбивается на квадратные элементы одинакового размера и каждый такой элемент описывается отдельно. Этот квадратный графический элемент называют пикселом (picture element, pixel).
Пиксель – наименьшая составляющая растровой графики. Один пиксель содержит в себе информацию о расположении по оси Х и Y , а так же информацию о цвете и прозрачности (альфа-канал).
Изображения, представленные посредством пикселей, называют растровыми, то есть разложенные на элементы.
Растровое изображение — это файл данных или структура, представляющая собой сетку пикселей на компьютерном мониторе или цветовых точек на бумаге и материалах.
Важными характеристиками для таких изображений являются:
- Количество пикселов — разрешение. Они могут указываться отдельно по ширине и высоте (640х480; 1024х768), но иногда указывается общее количество пикселов.
- Цветовое пространство (цветовая модель) RGB, CMYK, HSV и т.д.
- Количество используемых цветов или глубина цвета (эти характеристики имеют следующую зависимость: N = 2I , где N — количество цветов, а I — глубина цвета)
Разрешение
Наиболее распространенная единица измерения – dpi – количество пикселов на одном дюйме длины (1 дюйм = 2,54 см).
Но что да ет разрешение?
1 дюйм практически совпадает с 5ю клетками в тетради и если обвести их и закрасить одну клетку, то разрешение нашего «рисунка» будет 5 dpi .
Теперь уменьшим размер клетки-пикселя в 4 раза, закрасим только четверть клетки, в этом случае разрешение увеличится только в 2 раза, ведь на одну длину теперь приходится 10 клеток-пикселей
 | |
| разрешение 300 dpi | разрешение 72 dpi |
Глубина цвета — набор цветов, используемый для отображения изображения.
- цветные :
- HighColor – 16 бит на пиксель (65 536 цветов);
- True Color – 24 бит на пиксель (16,7 млн цветов);
- Deep Color – 32 (4 байт отвечает за прозрачность, или информацию об альфа-канале), 48 и более бит на пиксель;
Преимущества растрового изображения:
Источник
Векторное представление графической информации
Любой рисунок, состоящий из сложных фигур, можно разбить на более мелкие примитивные фигуры, которые в векторном способе кодирования хранятся в памяти компьютера в виде математических формул и геометрических примитивов, таких как круг, квадрат, эллипс и подобных фигур.
· чтобы закодировать круг следует указать компьютеру его радиус, координаты центра и цвет.
· для прямоугольника достаточно задать размеры сторон, координаты вершин и цвет;
· с помощью математических формул можно описать самые разные фигуры. Чтобы нарисовать более сложный рисунок, применяют несколько простых фигур.
· масштабирование изображения происходит с помощью математических операций, например, умножением параметров графических элементов на коэффициент масштабирования.
Основу векторных изображений составляют линии и кривые, называемые векторами или объектами, или контурами. Поэтому векторную графику часто называют объектно-ориентированной.
Каждый независимый объект можно редактировать, т .е :
Преимущества векторной графики:
1. Возможность неограниченного масштабирования изображения без потери качества и без увеличения размеров исходного файла (либо с незначительным увеличением размеров).
2. Легкость редактирования, т.к. изображение состоит из отдельных объектов, которые могут накладываться друг на друга, но остаются независимыми.
3. Высокая точность рисования (до сотой доли микрона).
4. Качество изображения на печати не зависит от исходного разрешения изображения, а определяется разрешающей способностью печатающих устройств (принтера, плоттера и т.п.).
5. Размеры векторных файлов имеют значительно меньший размер, чем файлы растровой графики.
6. Высокое качество печати рисунков и возможность преобразования векторного изображения в растровое как средствами графических редакторов, так и с помощью буфера обмена Windows .
Недостатки векторной графики:
1. Трудно осуществить экспорт изображения из растрового формата в векторный.
2. Ограниченность в живописных средствах, некоторая условность получаемых изображений. Так как все рисунки состоят из кривых, описанных формулами, трудно получить реалистичное изображение. Если попытаться описать фотографию математическими формулами, размер полученного файла окажется больше, чем соответствующего файла растровой графики.
3. Невозможность автоматизации ввода графической информации: не существует векторных мониторов и векторных сканеров.
4. Невозможность применения обширной библиотеки эффектов, используемых при работе с растровыми изображениями.
Сегодня ни один современный профессиональный графический пакет не является чисто векторным или чисто растровым, а совмещает в себе элементы обеих видов графики. Например, CorelDRAW имеет собственные и подключаемые инструменты для редактирования растровых изображений, в Adobe PhotoShop расширены возможности для работы с векторными объектами.
Структура векторной иллюстрации:
Структуру любой векторной иллюстрации можно представить в виде иерархического дерева.
В качестве примера рассмотрим изображение ветки с цветами.
1 Уровень структуры (Иллюстрация)
Иллюстрация =объекты +сегмент ы( узлы + линии) + заливки
2 Уровень – объекты, состояние из контуров. В большинстве редакторов для их отображения необходимо выбрать режим просмотра в виде каркаса.
Обычно все объекты в иллюстрации сгруппированы, поэтому для получения доступа к редактированию отдельных объектов иллюстрации их нужно сначала разгруппировать. Объекты иллюстрации состоят из одного или нескольких контуров.
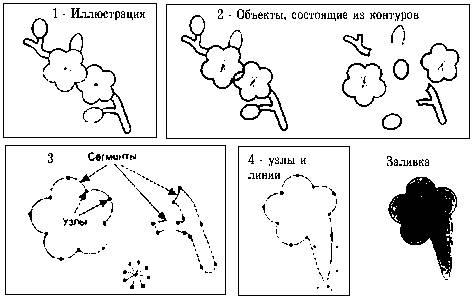
Контуром называется любая геометрическая фигура, созданная с помощью инструментов рисования векторной программы.
Открытый контур имеет четко обозначенные концевые точки. Синусоидальная линия, например, является открытым контуром. В данном примере открытыми контурами являются тычинки цветка.
Замкнутый контур — это замкнутая кривая, у которой начальная и конечная точки совпадают. Примером замкнутого контура является окружность. В некоторых редакторах замкнутый контур называют фигурой. В данном примере замкнутым контуром является форма цветка и форма стебля.
Замкнутые контуры имеют свойство заполнения цветом, текстурой или растровым изображением (картой).
Заливка — это цвет или узор, выводимый в замкнутой области, ограниченной кривой.
3 Уровень структуры — сегменты
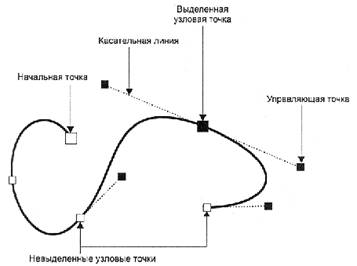
Каждый контур может состоять из одного или нескольких сегментов. Начало и конец каждого сегмента называют узлами, или опорными точками. Опорные точки соединены между собой линиями (прямыми или кривыми).
Перемещение узловых точек приводит к изменению формы контура. Уровень (самый нижний) уровень иерархии – узлы и отрезки линий, соединяющих между собой соседние узлы. Существует несколько типов линий и разновидностей узлов.
Любой из перечисленных здесь элементов иллюстрации, начиная от самой иллюстрации и кончая узлами и линиями, можно трактовать как объект. Поэтому термин «объект» используется в смысле элемента векторного рисунка.
В начале 70-х годов профессор Пьер Безье, проектируя на компьютере корпуса автомобилей «Рено», впервые применил для этой цели особый вид кривых, описываемых уравнением третьего порядка, которые впоследствии стали известными под названием кривые Безье.
В настоящее время кривые Безье присутствуют в любом современном графическом пакете. Все компьютерные шрифты состоят из кривых Безье.
Появление кривых Безье вызвало переворот в видео и трехмерной графике. До появления формул Безье контуры компьютерных персонажей были ломаными, поверхности – гранеными, а движения – прерывистыми, скачкообразными, неестественными.
Таким образом, кривая Безье используется в двух — , трехмерной графике, видео и анимации.
Основным элементом является узел (опорная точка). Каждый контур имеет несколько узлов. Сложный контур имеет множество узлов. Манипулируя узлами можно изменять форму контура. Под манипулированием узлами следует понимать:
· изменение свойств узлов;
· добавление или удаление узлов;
· при выделении узловой точки у нее появляются два управляющие точки, соединенные с узловой точкой касательными линиями. Начальная и конечная точки кривой имеют одну управляющую точку.
Таким образом, основными элементами кривой Безье являются:
· касательная в узловой точке.
Различают три типа узловых точек (узлов):
· Симметричный узел ( symmetrical node ) ;
· Гладкий узел ( smooth node ) ;
· Острый узел/узел излома/ ( cusp node ) .
Свойства симметричного узла:
Касательные по обе стороны от узловой точки имеют одинаковую длину и лежат на одной прямой. Это означает, что кривизна сегментов с обеих сторон узловой точки одинакова.
Изменение положения управляющей точки приводит к изменению угла наклона касательной к кривой и соответственно изменению кривизны сегментов.
Изменение длины касательной с одной стороны узловой точки приводит к аналогичному изменению длины касательной с другой стороны (их длины всегда равны – это свойство симметричного узла).
Если узел является Симметричным, то его кнопка приглушена, и его можно изменить на Узел излома или Гладкий узел .
Свойства гладкого узла:
Касательные линии по обе стороны от узловой точки лежат на 
одной прямой, но длина этих отрезков разная. Это означает, что кривизна криволинейных участков, прилегающих к узловой точке с разных сторон, не одинакова.
Изменение длины касательной линии с одной стороны приводит к изменению радиуса кривизны криволинейного сегмента с этой стороны от узловой точки, при этом длина второго отрезка касательной линии (с другой стороны узловой точки) не изменяется.
Если узел является Гладким, то его кнопка приглушена, и его можно 
изменить на Симметричный или Узел излома .
Свойства острого узла (узла излома):
У острого узла касательные линии с разных сторон узловой точки не лежат на одной прямой. Поэтому кривизна сегментов с разных сторон узловой точки неодинакова, и контур в этой точке имеет резкий излом.
Радиус кривизны и угол наклона касательной для каждого криволинейного сегмента с разных сторон узловой точки регулируются независимо друг от друга. В этом случае форма сегмента кривой будет регулироваться только одним отрезком касательной, а не двумя, как это было в предыдущих случаях.
Область применения векторной графики – создание и редактирование стилизованных изображений:
· плакаты и другая высококонтрастная графика;
· диаграммы и графики;
· логотипы и тексты с четкими и гладкими краями;
Для работы художнику за компьютером необходимо иметь как минимум одну программу для обработки растровых изображений и одну для обработки векторных изображений.
Сравнение растрового и векторного представления графической информации
Фрактальное представление графической информации
Фрактальная графика, как и векторная, – вычисляемая, но отличается от нее тем, что никакие объекты в памяти компьютера не хранятся. Изображение строится по уравнению, поэтому ничего, кроме формулы, хранить не нужно. Изменяются коэффициенты уравнения, и программа генерирует совершенно новую картину.
Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта « The Fractal Geometry of Nature ». В его работах использованы научные результаты других ученых, работавших в 1875-1925 годах в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф ). Но только в наше время удалось объединить их работы в единую систему.
Фракталом называется структура, состоящая из частей, которые подобны целому. Самоподобие – это свойство фракталов. Объект называют самоподобным , когда части объекта походят на сам объект и друг на друга.
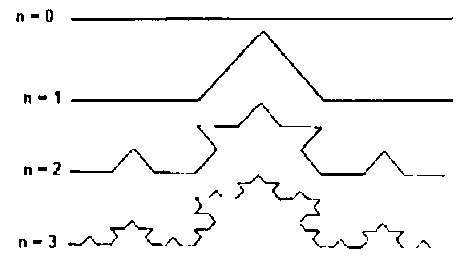
Геометрические фракталы получают с помощью некоторой ломаной (или поверхности), называемой генератором.
Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.
Благодаря фрактальной графике найден способ эффективной реализации сложных объектов, образы которых похожи на природные. С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря.
Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Они очень красивы, необычны и интересны. Вы сами задаете форму рисунка математической формулой. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.
// Демонстрация фрактальной графики. Поле из одуванчиков. Использование комплексной арифметики
Источник
