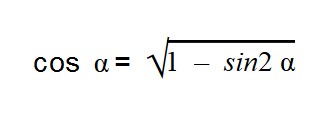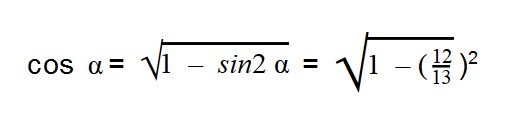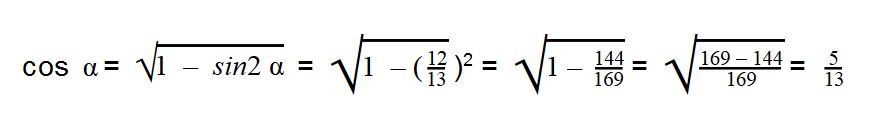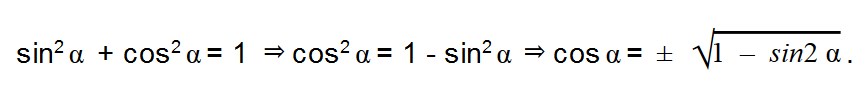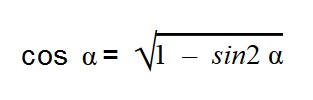- Как доказать тригонометрическое тождество?
- Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.
- Как доказывать тождество?
- Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
- Как доказать основное тригонометрическое тождество
- Ответы на часто задаваемые вопросы:
- Основное тригонометрическое тождество
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Примеры решения задач
Как доказать тригонометрическое тождество?
Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.
А вот выражение \(\frac
Как доказывать тождество?
Рецепт до одури прост:
Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
Для того, чтоб это сделать можно:
- Преобразовывать только правую или только левую часть.
- Преобразовывать обе части одновременно.
- Использовать любые допустимые математические преобразования (например, приводить подобные; раскрывать скобки; переносить слагаемые из одной части в другую, меняя знак; умножать или делить левую и правую часть на одно и то же число или выражение, не равное нулю и т.д.).
- Использовать любые математические формулы.
Именно четвертый пункт при доказательстве тождеств используется чаще всего, поэтому все формулы тригонометрии нужно знать, помнить и уметь использовать.
Пример. Доказать тригонометрическое тождество \(\sin2x=2\sinx\cdot \cos
Решение:
\(\sin2x=2 \sinx\cdot \cos
Будем преобразовывать левую часть.
Представим \(2x\) как \(x+x\)…
Левая часть равна правой – тождество доказано.
Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.
Применим в числителе вездесущие основное тригонометрическое тождество: \(\sin^2
Левая часть равна правой, тождество доказано.
Здесь будем преобразовывать только правую часть, стремясь свести ее к левой. Левую же оставляем неизменной. Вспоминаем формулу двойного угла для косинуса .
Теперь сделаем почленное деление в дроби (т.е. применим правило для сложения дробей в обратную сторону): \(\frac
Первую дробь правой части сократим, а ко второй применим свойство степени : \(\frac
Ну, а синус деленный на косинус равен тангенсу того же угла:
Левая часть равна правой, тождество доказано.
Здесь будем преобразовывать обе части:
— в левой: преобразуем \(\cos2t\) по формуле двойного угла;
— а в правой \(ctg(π+t)\) по формуле приведения .
Теперь работаем только с левой частью.
В числителе воспользуемся формулой сокращенного умножения , в знаменателе вынесем за скобку синус.
Сократим дробь на \(\cos<t>+\sin<t>\).
Почленно разделим дробь, превратив ее в две отдельные дроби.
Первая дробь это котангенс , а вторая равна единице.
Левая часть равна правой, тождество доказано.
Как видите, все довольно несложно, но надо знать все формулы и свойства.
Как доказать основное тригонометрическое тождество
Два простых способа вывести формулу \(\sin^2x+\cos^2x=1\). Нужно знать только теорему Пифагора и определение синуса и косинуса.
Ответы на часто задаваемые вопросы:
Вопрос: Как определить, что в тождестве надо преобразовывать – левую часть, правую или обе вместе?
Ответ: Нет никакой разницы – в любом случае вы получите один и тот же результат. Например, в третьем примере мы легко могли бы получить из левой части \(1-tg^2 t\) правую \(\frac
Источник
Основное тригонометрическое тождество
О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.
Образовался прямоугольный треугольник OA1B.
|OB| = |x|.
Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB| 2 = |OA1| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .
Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α =
=
- ctg α =
=
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
ctg α = x/y
 и
и  ,
, получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg 2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg 2 α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =.
- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
Вычисляем:
Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
Таким же образом, используя формулу, вычисляем значение котангенса:

Задачка 2. Найдите значение cos α,
если:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
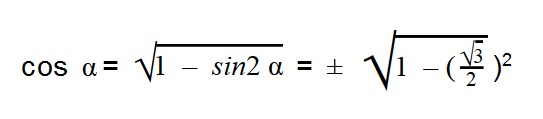

Подставляем значения sin α:
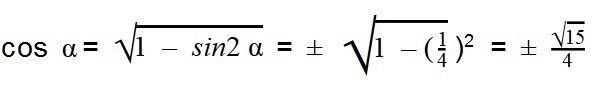
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Источник





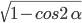
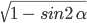
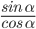
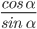
 =
= 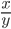 =
= 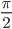 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.