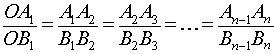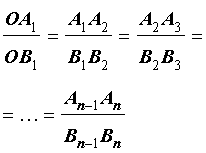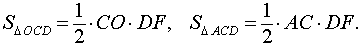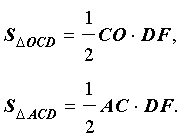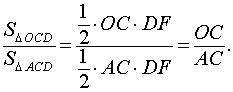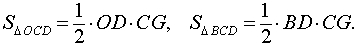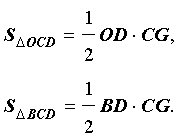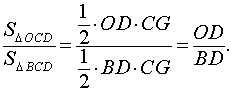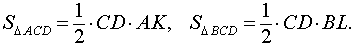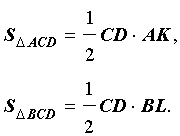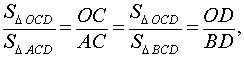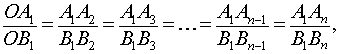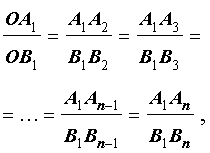- Президентский ФМЛ №239
- Инструменты пользователя
- Инструменты сайта
- Содержание
- Теорема Фалеса
- Доказательство
- Рассмотрим случай, когда прямые a и b параллельны.
- Рассмотрим случай, когда прямые a и b не параллельны.
- Замечание
- Теорема Фалеса
- Формулировка теоремы Фалеса
- Примеры решения задач
- Историческая справка
- Президентский ФМЛ №239
- Инструменты пользователя
- Инструменты сайта
- Содержание
- Теорема Фалеса
- Доказательство
- Рассмотрим случай, когда прямые a и b параллельны.
- Рассмотрим случай, когда прямые a и b не параллельны.
- Замечание
- Теорема Фалеса
- 4.6. Обобщенная теорема Фалеса. Пропорции. Масштаб
Президентский ФМЛ №239
Инструменты пользователя
Инструменты сайта
Содержание
Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равных отрезков, а потом через их концы провести параллельные прямые, то они отсекут на другой прямой равные отрезки.
Доказательство
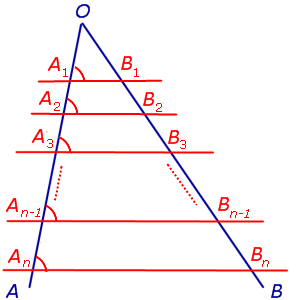
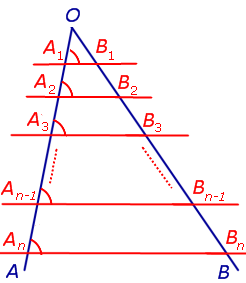
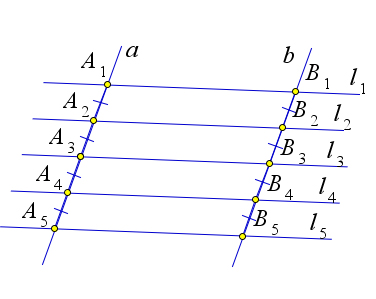
Пусть параллельные прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно.
Пусть при этом $A_1A_2=A_2A_3$.
Докажем, что тогда $B_1B_2=B_2B_3$.
Рассмотрим случай, когда прямые a и b параллельны.
Тогда $A_2A_1B_1B_2$ и $A_3A_2B_2B_3$ – параллелограммы.
Следовательно, $A_1A_2=B_1B2$ и $A_2A_3=B_2B_3$, и так как $A_1A_2=A_2A_3$, то $B_1B_2=B_2B_3$.
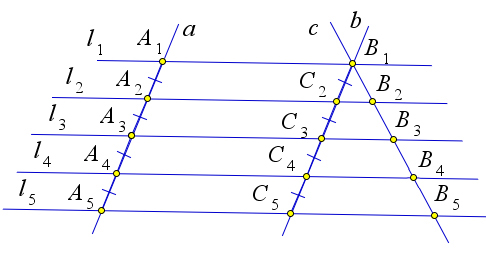
Рассмотрим случай, когда прямые a и b не параллельны.
Проведем через точку $B_1$ прямую $c$, параллельную прямой $a$.
Пусть прямые $l_2,l_3,l_4$ и прямая $c$ пересекаются в точках $C_2, C_3, C_4$.
По первому случаю $B_1C_2=C_2C_3$, кроме того $B_2C_2\parallel B_3C_3$.
Тогда $B_2C_2$ – средняя линия $\triangle B_1C_3B_3$, то есть $B_1B_2=B_2B_3$.
Замечание
Утверждение обратное теореме Фалеса неверно.
То есть, из того, что прямые прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно, и при этом $A_1A_2=A_2A_3$ и $B_1B_2=B_2B_3$, не следует, что прямые $l_1, l_2$ и $l_3$ параллельны.
Источник
Теорема Фалеса
Формулировка теоремы Фалеса
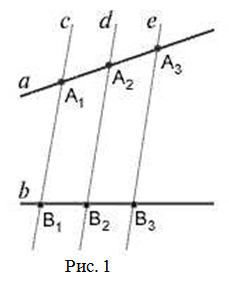
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
Обобщённая теорема Фалеса
Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Обратная теорема Фалеса
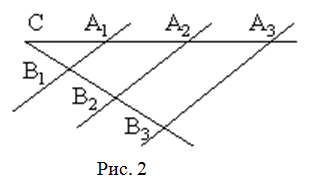
Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).
Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.
Примеры решения задач
Задание. Разделить данный отрезок на четыре равные части.
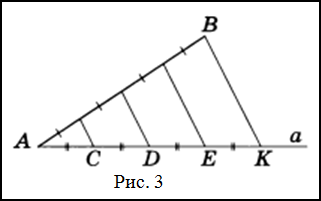
Решение. Пусть $AB$ — заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.
Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .
Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .
Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.
Теорема Фалеса не по зубам? Тебе ответит эксперт через 10 минут!
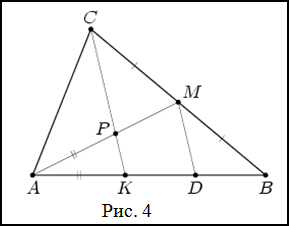
Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .
Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).
По теореме Фалеса $BD = KD$ .
По теореме о пропорциональных отрезках имеем, что
$$P M=K D=\frac <2>\Rightarrow B K: P M=2: 1$$
Ответ. $B K: P M=2: 1$
Историческая справка
Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.
Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.
Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Источник
Президентский ФМЛ №239
Инструменты пользователя
Инструменты сайта
Содержание
Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равных отрезков, а потом через их концы провести параллельные прямые, то они отсекут на другой прямой равные отрезки.


Доказательство
Пусть параллельные прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно.
Пусть при этом $A_1A_2=A_2A_3$.
Докажем, что тогда $B_1B_2=B_2B_3$.
Рассмотрим случай, когда прямые a и b параллельны.
Тогда $A_2A_1B_1B_2$ и $A_3A_2B_2B_3$ – параллелограммы.
Следовательно, $A_1A_2=B_1B2$ и $A_2A_3=B_2B_3$, и так как $A_1A_2=A_2A_3$, то $B_1B_2=B_2B_3$.
Рассмотрим случай, когда прямые a и b не параллельны.
Проведем через точку $B_1$ прямую $c$, параллельную прямой $a$.
Пусть прямые $l_2,l_3,l_4$ и прямая $c$ пересекаются в точках $C_2, C_3, C_4$.
По первому случаю $B_1C_2=C_2C_3$, кроме того $B_2C_2\parallel B_3C_3$.
Тогда $B_2C_2$ – средняя линия $\triangle B_1C_3B_3$, то есть $B_1B_2=B_2B_3$.
Замечание
Утверждение обратное теореме Фалеса неверно.
То есть, из того, что прямые прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно, и при этом $A_1A_2=A_2A_3$ и $B_1B_2=B_2B_3$, не следует, что прямые $l_1, l_2$ и $l_3$ параллельны.
Источник
Теорема Фалеса
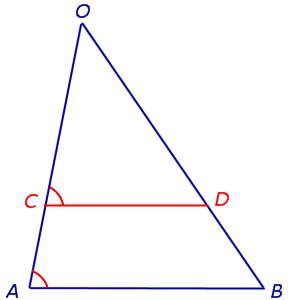
Теорема Фалеса . Через произвольные точки
лежащие на стороне AO угла AOB (рис.1), проведены параллельные прямые, пересекающие сторону угла OB в точках
соответственно. Тогда справедливы равенства
Доказательство . Докажем сначала следующую лемму.
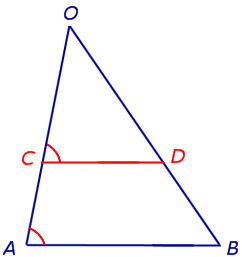
Лемма . Через произвольную точку C , лежащую на стороне OA треугольника OAB , проведена прямая, параллельная прямой AB и пересекающая сторону OB в точке D (рис.2).
Тогда справедливо равенство
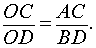 | (1) |
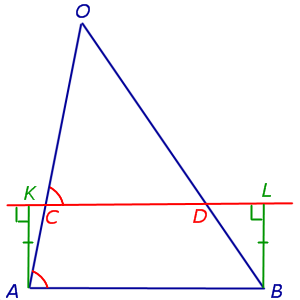
Доказательство леммы . Опустим из точек A и B перпендикуляры AK и BL на прямую CD (рис.3). Заметим, что эти перпендикуляры равны, поскольку AKLB – прямоугольник прямоугольник .
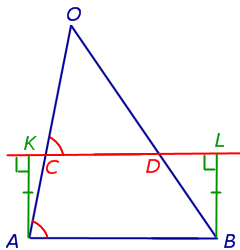
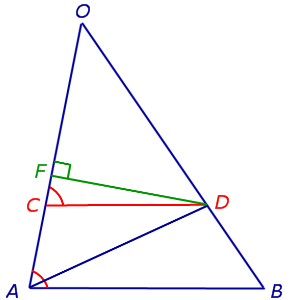
Из точки D опустим перпендикуляр DF на прямую OA (рис.4).
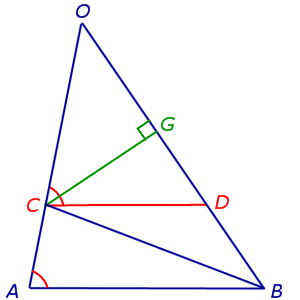
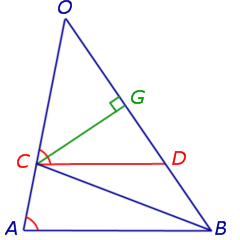
Из точки C опустим перпендикуляр CG на прямую OB (рис.5).
В соответствии с рисунком 4 площади треугольников OCD и ACD можно вычислить по формулам
В соответствии с рисунком 5 площади треугольников OCD и BCD можно вычислить по формулам
Кроме того, заметим, что площади треугольников ACD и BCD равны. Действительно, в соответствии с рисунком 3 справедливы формулы
откуда получаем цепочку равенств
что и завершает доказательство леммы.
Воспользовавшись леммой, заметим (рис.1), что из равенства (1) вытекают равенства
откуда на основе свойств производных пропорций, заключаем, что справедливы равенства
что и завершает доказательство теоремы Фалеса.
Следствие . Если через точки
лежащие на стороне AO угла AOB (рис.6) и удовлетворяющие условию
проведены параллельные прямые, пересекающие сторону угла OB в точках
Источник
4.6. Обобщенная теорема Фалеса. Пропорции. Масштаб
Пропорции
называется пропорцией. При этом говорят, что:
отношение чисел x1 и x2 равно отношению чисел y1 и y2,
числа x1 и y1 (!) пропорциональны числам x2 и y2 (то есть числители пропорциональны знаменателям).
Входящие сюда числа x1, x2, y1 и y2 называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.
Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x1 из левой части в правую. Для этого умножим обе части пропорции на 1/x1:
В результате получаем
то есть переменная x1 у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y2. Это достигается умножением на нее обеих частей данного равенства. В результате имеем
Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве
числители x1 и y1 соотносятся между собой точно так же, как и соответствующие им знаменатели x2 и y2.
Обобщенная теорема Фалеса
Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.
Тогда длины отсекаемых отрезков образуют следующую пропорцию
Докажем эту теорему в случае, когда отношение длин
представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби
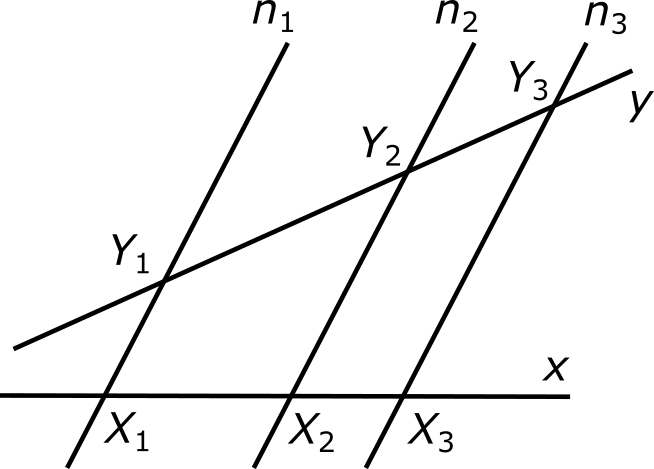
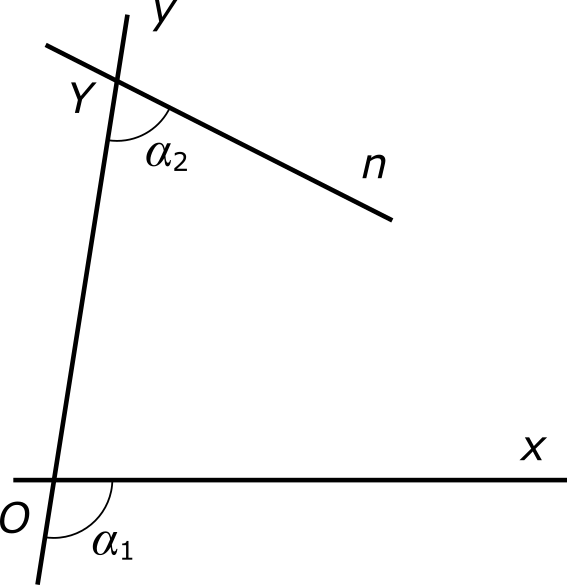
где a и b — некоторые натуральные числа, a α 1 > α 2, как показано на рисунке.
Проведем через точку O прямую n1, параллельную прямой n. Отметим на ней со стороны угла α 1 произвольную точку N1 и проведем через эту точку прямую y1, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.
Это значит, что прямая y1 пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N1N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N1N через X1. Проведем через нее прямую n2, параллельную прямой n. Эта прямая разбивает параллелограмм ON1NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y1. Отметим на прямой x такую точку X, для которой выполняется соотношение
Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n2, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.
Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:
(1) Угол между прямыми a и b равен нулю.
(2) Прямые a и b нигде не пересекаются.
(3) Прямые a и b параллельны.
В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.
Конспект
1. Равенство вида x1/x2 = y1/y2 называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x1/y1 = x2/y2.
2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.
3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n1 и n2. Тогда отрезки, отсекаемые на прямых n1 и n2, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n1 и n2.
4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.
5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.
6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.
Источник