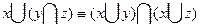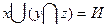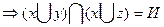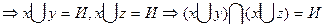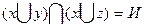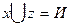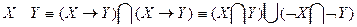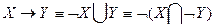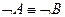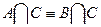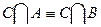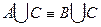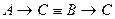Доказательство равносильностей



Доказательство равносильностей можно осуществить двумя способами:
· с помощью таблицы истинности;
· с помощью рассуждений.
Пример (Задание №6): докажем равносильность
а) с помощью таблицы.
| X | Y | Z | 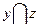 | 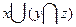 | 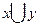 | 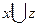 | 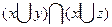 |
Мы видим в 5-ом и 8-ом столбцах получили одинаковые значения, тем самым мы доказали равносильность данной формулы.
б) с помощью рассуждений.
1. допустим истинность левой части
2. установим истинное значение для всех истинностных переменных, входящих в список или оценку списка
3. оценку списка подставим в правую часть равносильности
4. установим истинность для правой части
5. все повторим справа налево.
I.
х=И или 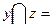
если х=И 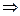
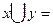
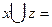
если 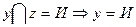
II.
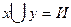
х =И или y =И и х=И или z=И
если х=И 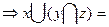
если y=И и z=И 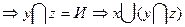
(И – «истина», т. е. присваивается истинное значение)
В процессе доказательства равносильностей может возникнуть необходимость перехода от одной равносильности к другой. Осуществляется переход можно заменой одних логических связок на другие.
Правила перехода от одних равносильностей к другим
Пусть 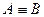
1.
2.
3.
4.
5.
6. С А 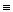
Правила равносильных преобразований
Пусть 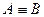
До настоящего момента было определено понятие равносильности формул алгебры высказываний.
Понятие равносильности функций алгебры логики определяется аналогично.
Пусть f и g — функции алгебры логики, x1,…,xn — совокупность аргументов, входящих хотя бы в одну из этих функций, говорят, что f и g- равносильны, если при всех значениях x1,…,xn значения f и g — совпадают.
Формула А называется тождественно истинной, если на любом списке переменных она принимает значение «Истина».
Тавтология – это утверждение, которое всегда истинно, иначе ее определяют как закон.
Формула называется тождественно ложной, если на любом списке переменных она принимает значение «Ложь».
Противоречие – это утверждение, которое всегда ложно. Таблица истинности для противоречия всегда принимает значение «Ложь».
| А | ||
| И | Л | Л |
| Л | И | Л |
Формула А называется выполнимой, если находится такой набор переменных, что она принимает значение «Истина».
Формула А называется опровержимой, если находится такой набор переменных, что она принимает значение «Ложь».
Что касается высказываний, то здесь применяется термин высказывание логически истинно, такое высказывание можно получить путем его подстановки в тавтологию (например: предложение «Если идет дождь или идет снег, и не идет дождь, то идет снег» получим путем подстановки в тавтологию и высказывание логически ложно, если его подставляют в противоречие.
Источник
Способы доказательства равносильности формул
Равносильные формулы алгебры логики
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A ≡ B .
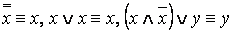
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр., 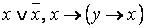
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., 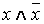
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A ↔ B тавтология, и обратно, если формула A ↔ B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· 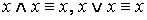
· 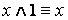
· 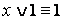
· 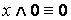
· 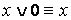
· 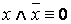
· 
· 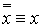
· 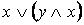
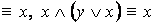
1. Равносильности, выражающие одни логические операции через другие:
· 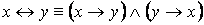
· 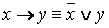
· 
· 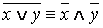
· 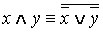
· 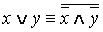
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как 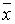
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x | y ≡ 
Логические значения связки Шеффера описываются следующей таблицей истинности:
Имеют место следующие равносильности: а) 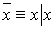
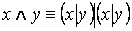
2) Связка Лукасевича – конъюнкция отрицаний.
Обозначение . x ↓ y ≡ 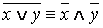
Логические значения связки Лукасевича описываются следующей таблицей истинности:
2. Равносильности, выражающие основные законы алгебры логики:
· 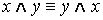
· 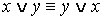
· 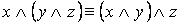
· 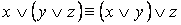
· 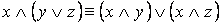
· 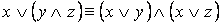
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
Равносильные преобразования формул
Используя равносильности групп 1–3 можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.
Равносильные преобразования используются для доказательства равносильностей , для приведения формул к заданному виду, для упрощения формул. Формула A считается проще равносильной ей формулы B , если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции, а отрицание относят к элементарным высказываниям.
Источник