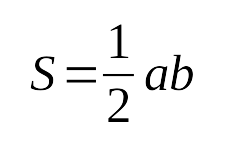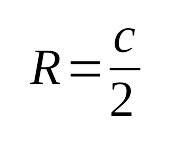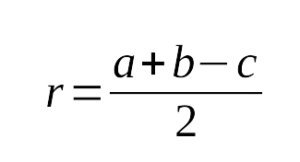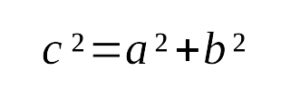Способы доказательства прямоугольного треугольника

Прямоугольный треугольник: Признаки Равенства и Подобия

Определение

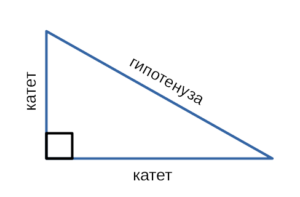
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

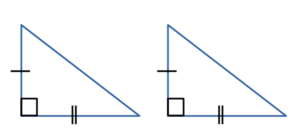
1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
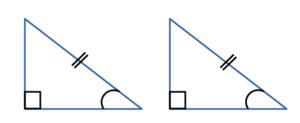
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
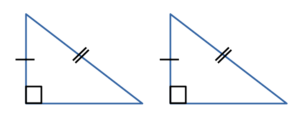
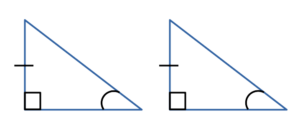
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Источник

Как доказать, что треугольник прямоугольный

Здравствуйте! Я к Вам снова с просьбой в помощи доказательства. В данном случае — я не могу понять как доказать, что треугольник прямоугольный. Даже дана задачка на эту тему. В треугольнике FCH проведена медиана HE , HE=FE=EC.Доказать что треугольник прямоугольный.

Здравствуйте.
Давайте сначала вспомним, какой треугольник называется прямоугольным. Так вот прямоугольным называется тот треугольник, угол которого равен .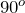
Чтоб понять, как доказать, что треугольник прямоугольный, надо знать, каким свойствами он обладает. Ведь одного знания про угол 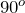бывает недостаточно. так как про это не всегда скажется в условии.
Так вот, прямоугольный треугольник обладает такими свойствами:

1. Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
2. Медиана прямоугольного треугольника равна половины гипотенузы
3. сумма двух острых углов прямоугольного треугольника равна 90 градусов
4. Сумма всех углов в треугольнике равна 180 градусов
5. прямой угол всегда равен 90 градусов
6. катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы
7. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусам

Давайте разберёмся с Вашей задачкой. Так как нам не сказано, какой это треугольник, то попробуем это доказать. Единственное, что мы знаем, так это то, что его медиана равна половине стороны. Теперь вспоминаем свойство прямоугольного треугольника, в котором проведена медиана. И мы знаем, что именно в прямоугольном треугольнике, медиана проведённая к гипотенузе равна половине гипотенузы. Так вот, это свойство у нас с вами выполняется и выходит, что сторона — гипотенуза, которую медиана делить пополам.
Так что, вот мы с Вами и доказали, что наш треугольник прямоугольный.

Источник

Теорема Пифагора

О чем эта статья:

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

• если c 2 2 + b 2 , значит угол, обращенный к стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, обращенный к стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, обращенный к стороне c, является тупым.

Записывайтесь на обучение по математике для учеников с 1 по 11 классы!

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

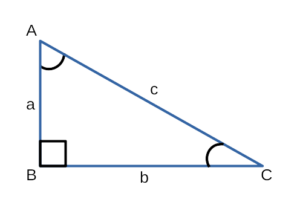
Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?

значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Источник

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Источник