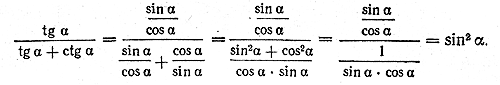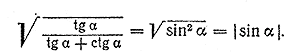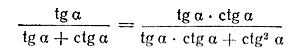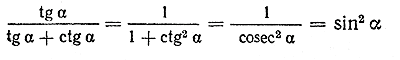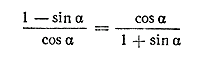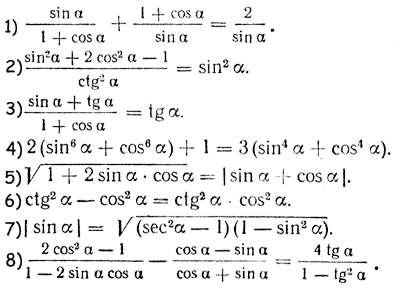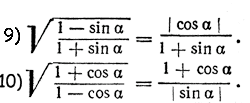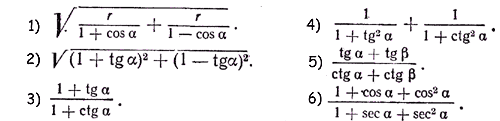Способы доказательств тригонометрических тождеств

Доказательство тригонометрических тождеств

При доказательстве любых тождеств, и в частности тригонометрических, обычно используют следующие способы:

1) выражение, стоящее и одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства;

2) выражения, стоящие в левой и правой частях тождества, с помощью тождественных преобразований приводят к одному и тому же виду;

3) доказывают, что разность между левой и правой частями данного тождества равна нулю.

Поясним это на некоторых частных примерах.

Пример 1. Доказать тождество

sin 4 α — cos 4 α = sin 2 α — cos 2 α .

Используя формулу для разности квадратов двух чисел, получаем:

sin 4 α — cos 4 α = (sin 2 α + cos 2 α) (sin 2 α — cos 2 α).

Ho sin 2 α + cos 2 α = 1. Поэтому

sin 4 α — cos 4 α = sin 2 α — cos 2 α, что и требовалось доказать.

Пример 2. Доказать тождество

Это тождество мы будем доказывать путем преобразования выражения, стоящего в правой части.

Поэтому

Прежде всего заметим, что ctg α =/= 0; в противном случае не имело бы смысла выражение tg α = 1 /_ctg _α. Но если ctg α =/= 0, то числитель и знаменатель подкоренного выражения можно умножить на ctg α, не изменяя значения дроби. Следовательно,

Используя тождества tg α • ctg α = 1 и 1+ ctg 2 α = cosec 2 α , получаем

Поэтому 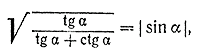что и требовалось доказать.

Замечание. Следует обратить внимание на то, что левая часть доказанного тождества (sin α) определена при всех значениях α, а правая — лишь при α =/= π /₂n.

Поэтому только при всех допустимых значениях α 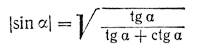Вообще же эти выражения не эквивалентны друг другу.

Пример 3. Доказать тождество

Преобразуем левую и правую части этого тождества, используя формулы приведения:

Итак, выражения, стоящие в обеих частях данного тождества, приведены к одному и тому же виду. Тем самым тождество доказано.

Пример 4. Доказать тождество

Покажем, что разность между левой и правой частями. данного тождества равна нулю.

= (sin 2 α + cos 2 α) 2 — 1 = 1 — 1 = 0.

Тем самым тождество доказано.

Пример 5. Доказать тождество

Это тождество можно рассматривать как пропорцию. Но чтобы доказать справедливость пропорции a /_b = c /_d, достаточно показать, что произведение ее крайних членов ad равно произведению ее средних членов bc. Так мы поступим и в данном случае. Покажем, что (1 — sin α) (1+ sin α) = cos α • cos α.

По поводу этого примера можно было бы сделать замечание, аналогичное замечанию к примеру 2.

I . Доказать тождества

II . Упростить выражения

1). Найти значение выражения 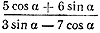, если известно, что tg α = 1 /₃

2). Найти значение выражения 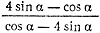, если известно, что котангенс угла α не определен.

3). Найти значение выражения 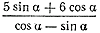, если известно, что ctg α = 1 /₂

Источник

Как доказать тригонометрическое тождество?

Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.

А вот выражение \(\frac=x\) является тождеством только при условии \(x≠0\) (иначе левая часть не существует).

Как доказывать тождество?

Рецепт до одури прост:

Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».

Для того, чтоб это сделать можно:

Преобразовывать только правую или только левую часть.
Преобразовывать обе части одновременно.
Использовать любые допустимые математические преобразования (например, приводить подобные; раскрывать скобки; переносить слагаемые из одной части в другую, меняя знак; умножать или делить левую и правую часть на одно и то же число или выражение, не равное нулю и т.д.).
Использовать любые математические формулы.

Именно четвертый пункт при доказательстве тождеств используется чаще всего, поэтому все формулы тригонометрии нужно знать, помнить и уметь использовать.

Пример. Доказать тригонометрическое тождество \(\sin⁡2x=2\sin⁡x\cdot \cos\)
Решение:

\(\sin⁡2x=2 \sin⁡x\cdot \cos \)

Будем преобразовывать левую часть.
Представим \(2x\) как \(x+x\)…

Левая часть равна правой – тождество доказано.

Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.

Применим в числителе вездесущие основное тригонометрическое тождество: \(\sin^2⁡+\cos^2<⁡x>=1\).

Левая часть равна правой, тождество доказано.

Здесь будем преобразовывать только правую часть, стремясь свести ее к левой. Левую же оставляем неизменной. Вспоминаем формулу двойного угла для косинуса .

Теперь сделаем почленное деление в дроби (т.е. применим правило для сложения дробей в обратную сторону): \(\frac\) \(=\) \(\frac\) \(+\) \(\frac\)

Первую дробь правой части сократим, а ко второй применим свойство степени : \(\frac\) \(=\) \((\frac)^n\) .

Ну, а синус деленный на косинус равен тангенсу того же угла:

Левая часть равна правой, тождество доказано.

Здесь будем преобразовывать обе части:
— в левой: преобразуем \(\cos⁡2t\) по формуле двойного угла;
— а в правой \(ctg(π+t)\) по формуле приведения .

Теперь работаем только с левой частью.
В числителе воспользуемся формулой сокращенного умножения , в знаменателе вынесем за скобку синус.

Сократим дробь на \(\cos<⁡t>+\sin<⁡t>\).

Почленно разделим дробь, превратив ее в две отдельные дроби.

Первая дробь это котангенс , а вторая равна единице.

Левая часть равна правой, тождество доказано.

Как видите, все довольно несложно, но надо знать все формулы и свойства.

Как доказать основное тригонометрическое тождество

Два простых способа вывести формулу \(\sin^2x+\cos^2x=1\). Нужно знать только теорему Пифагора и определение синуса и косинуса.

Ответы на часто задаваемые вопросы:

Вопрос: Как определить, что в тождестве надо преобразовывать – левую часть, правую или обе вместе?
Ответ: Нет никакой разницы – в любом случае вы получите один и тот же результат. Например, в третьем примере мы легко могли бы получить из левой части \(1-tg^2 t\) правую \(\frac\) (попробуйте сделать это сами). Или преобразовывать обе, с тем чтоб они «встретились посередине», где-то в районе \(\frac<\cos^2⁡t-\sin^2⁡t><\cos^2⁡t>\) \(=\) \(\frac<\cos^2⁡t-\sin^2⁡t><\cos^2⁡t>\) . Поэтому вы можете доказывать любым удобным вам способом. Какую «тропинку» видите – по той и идите. Главное только – преобразовывайте «законно», то есть понимайте на основании какого свойства, правила или формулы вы делаете очередное преобразование.

Читайте также: Лучшие народные способы лечения геморроя
Источник

Основные тригонометрические тождества: их формулировки и вывод

В статье подробно рассказывается об основных тригонометрических тождествах. Эти равенства устанавливают связь между sin , cos , t g , c t g заданного угла. При известной одной функции можно через нее найти другую.

Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.

sin 2 α + cos 2 α = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α

Связь между sin и cos одного угла

Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.

sin 2 α + cos 2 α = 1

Заданные равенства t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α выводят из основного путем деления обеих частей на sin 2 α и cos 2 α . После чего получаем t g α = sin α cos α , c t g α = cos α sin α и t g α · c t g α = 1 — это следствие определений синуса, косинуса, тангенса и котангенса.

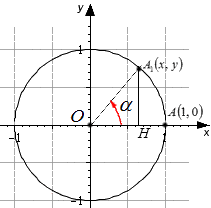
Равенство sin 2 α + cos 2 α = 1 является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .

Пусть даны координаты точки А ( 1 , 0 ) , которая после поворота на угол α становится в точку А 1 . По определению sin и cos точка А 1 получит координаты ( cos α , sin α ) . Так как А 1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x 2 + y 2 = 1 этой окружности. Выражение cos 2 α + sin 2 α = 1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α .

В тригонометрии выражение sin 2 α + cos 2 α = 1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.

Используя единичную окружность, поворачиваем точку А с координатами ( 1 , 0 ) вокруг центральной точки О на угол α . После поворота точка меняет координаты и становится равной А 1 ( х , у ) . Опускаем перпендикулярную прямую А 1 Н на О х из точки А 1 .

На рисунке отлично видно, что образовался прямоугольный треугольник О А 1 Н . По модулю катеты О А 1 Н и О Н равные, запись примет такой вид: | А 1 H | = | у | , | О Н | = | х | . Гипотенуза О А 1 имеет значение равное радиусу единичной окружности, | О А 1 | = 1 . Используя данное выражение, можем записать равенство по теореме Пифагора: | А 1 Н | 2 + | О Н | 2 = | О А 1 | 2 . Это равенство запишем как | y | 2 + | x | 2 = 1 2 , что означает y 2 + x 2 = 1 .

Используя определение sin α = y и cos α = x , подставим данные угла вместо координат точек и перейдем к неравенству sin 2 α + cos 2 α = 1 .

Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin 2 α + cos 2 = 1 относительно sin и cos , тогда получим выражения вида sin α = ± 1 — cos 2 α и cos α = ± 1 — sin 2 α соответственно. Величина угла α определяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.

Читайте также: Способы решения логарифмических уравнений с примерами презентация
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1 . Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.

Тангенс и котангенс через синус и косинус

Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.

t g α = sin α cos α c t g α = cos α sin α

Из определения синус является ординатой у , а косинус – абсциссой x . Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:

t g α = y x = sin α cos α , а выражение котангенса имеет обратное значение, то есть

c t g α = x y = cos α sin α .

Отсюда следует, что полученные тождества t g α = sin α cos α и c t g α = cos α sin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.

Отметим, что t g α = sin α cos α и c t g α = cos α sin α верны для любого значение угла α , значения которого входят в диапазон. Из формулы t g α = sin α cos α значение угла α отлично от π 2 + π · z , а c t g α = cos α sin α принимает значение угла α , отличные от π · z , z принимает значение любого целого числа.

Связь между тангенсом и котангенсом

Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как t g α · c t g α = 1 . Оно имеет смысл при α с любым значением, кроме π 2 · z , иначе функции будут не определены.

Формула t g α · c t g α = 1 имеет свои особенности в доказательстве. Из определения мы имеем, что t g α = y x и c t g α = x y , отсюда получаем t g α · c t g α = y x · x y = 1 . Преобразовав выражение и подставив t g α = sin α cos α и c t g α = cos α sin α , получим t g α · c t g α = sin α cos α · cos α sin α = 1 .

Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.

Тангенс и косинус, котангенс и синус

Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α .

Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1 , а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin 2 α + cos 2 α = 1 , можно разделить соответствующие стороны на cos 2 α и получить t g 2 α + 1 = 1 cos 2 α , где значение cos 2 α не должно равняться нулю. При делении на sin 2 α получим тождество 1 + c t g 2 α = 1 sin 2 α , где значение sin 2 α не должно равняться нулю.

Из приведенных выражений получили, что тождество t g 2 α + 1 = 1 cos 2 α верно при всех значениях угла α , не принадлежащих π 2 + π · z , а 1 + c t g 2 α = 1 sin 2 α при значениях α , не принадлежащих промежутку π · z .

Источник