Способы доказательств теоремы фалеса

Теорема Фалеса. Доказательство

Теорема 1 (Теорема Фалеса) . Пусть через точки \( \small A, \ B, \ C, D \) расположенные на одной стороне угла проведены параллельные прямые, которые пересекают другую сторону этого угла в точках \( \small A_1, \ B_1, \ C_1, D_1, \) соответственно. Тогда если равны отрезки \( \small AB \) и \( \small CD, \) то равны и отрезки \( \small A_1B_1 \) и \( \small C_1D_1. \)

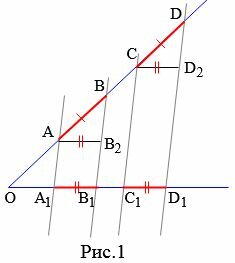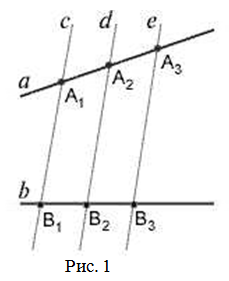
Доказательство. Пусть \( \small AB=CD \) и пусть прямые \( \small AA_1, \ BB_1, \ CC_1, DD_1 \) параллельны (Рис.1). Докажем, что \( \small A_1B_1=C_1D_1. \) Проведем прямые \( \small AB_2 \) и \( \small CD_2 \) параллельно стороне \( \small OD_1. \) Получили два четырехугольника \( \small AB_2B_1A_1 \) и \( \small CD_2D_1C_1. \) Эти четырехугольники являются параллелограммами поскольку противоположные стороны этих четырехугольников параллельны. Тогда

\( \small AB_2=A_1B_1, \) \( \small CD_2=C_1D_1. \)

(1)

Углы \( \small BAB_2 \) и \( \small DCD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small AB_2 \) и \( \small CD_2 \) секущей \( \small AD \) (см. статью Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда

Углы \( \small ABB_2 \) и \( \small CDD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small BB_2 \) и \( \small DD_2 \) секущей \( \small AD. \) Тогда

Треугольники \( \small ABB_2 \) и \( \small CDD_2 \) равны по второму признаку равенства треугольников так как \( \small AB=CD \) и выполнены равенства (2) и (3). Следовательно \( \small AB_2 = CD_2. \) Отсюда, учитывая (1) получим: \( \small A_1B_1=C_1D_1. \) Теорема доказана.

Источник

Обобщённая теорема Фалеса

Вы будете перенаправлены на Автор24

Основные понятия

Прежде чем сформулировать теорему Фалеса и доказать её, напомним несколько ключевых определений геометрии:

Четырёхугольник имеет четыре вершины.

Параллелограмм — это четырёхугольник, противоположные стороны которого попарно параллельны друг другу. В параллелограмме равны противоположные стороны между собой и противоположные углы.

Трапеция — это такой четырёхугольник, у которого две противоположные стороны параллельны друг другу, а две другие противоположные стороны не параллельны друг другу.

В целях понимания, приведём примеры задач с параллелограммом и трапецией.

Задача. Найти углы параллелограмма $ABCD$, если $\angle A=73^<\circ>$.

Решение. Сделаем такой рисунок:

Рисунок 1. Параллелограмм. Автор24 — интернет-биржа студенческих работ

На рисунке проведена прямая, параллельная $AB$ из вершины $B$. Угол, образованный вершиной $B$, проведённой прямой и стороной $BC$ равен $73^<\circ>$ как накрест лежащий относительно $\angle A$. По определению развернутого угла (развёрнутый угол равен $180^<\circ>$) получаем простые вычисления:

$\angle B=180-73=107^<\circ>$. Так как в параллелограмме противоположные углы равны, то $\angle C=\angle A=73^<\circ>, \angle D=\angle B=107^<\circ>$.

В примере выше можно было решить через свойство четырёхугольников о том, что сумма углов выпуклого четырёхугольника равна $360^<\circ>$. Для этого нужно было бы дополнительно доказать, что параллелограмм — это выпуклый четырёхугольник. Этот простой вопрос останется читателю для размышлений на досуге.

Задача. Найти $\angle B$ и $\angle D$ в трапеции $ABCD$, если $\angle A = 47^<\circ>, \angle C = 108^<\circ>$.

Решение. Сделаем рисунок:

Рисунок 2. Трапеция. Автор24 — интернет-биржа студенческих работ

На рисунке проведена прямая, параллельная $AB$ из вершины $B$. Угол, образованный вершиной $B$, проведённой прямой и стороной $BC$ равен $47^<\circ>$ как накрест лежащий относительно $\angle A$. По определению развернутого угла получаем простые вычисления: $\angle B=180-47=133^<\circ>$.

На рисунке также проведена прямая параллельно $CD$ из вершины $D$. Угол, образованный вершиной $D$, проведённой прямой и стороной $CD$ равен $108^<\circ>$ как накрест лежащий относительно $\angle С$. По определению развернутого угла получаем простые вычисления: $\angle B=180-108=72^<\circ>$.

Готовые работы на аналогичную тему

Как и в случае параллелограмма, данную задачу можно проверить, сложив все углы данной трапеции. Их сумма должна быть равна $360^<\circ>$. Можно убедиться, что сумма всех углов данной трапеции действительно равна $360$.

Владея ключевыми понятиями, можем перейти к теореме Фалеса и её доказательству.

Теорема Фалеса

Теорема названа в честь древнегреческого ученого Фалеса Милетского. Звучит она следующим образом:

Если последовательно отложить на прямой несколько равных друг другу отрезков и провести через их концы параллельные прямые, которые пересекают вторую проведённую прямую, то эти параллельные прямые отсекут на ней также равные отрезки.

Доказательство теоремы Фалеса

Докажем эту теорему.

Рисунок 3. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

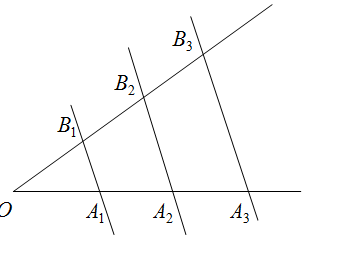
На прямой $a$ отложены следующие отрезки: $A_1 A_2, A_2 A_3, A_3 A_4. $. Через эти отрезки проведены несколько параллельных прямых, пересекающих прямую $b$ в соответствующих точках $B_1,B_2,B_3,B_4. $. Докажем, что отрезки $B_1 B_2, B_2 B_3, B_3 B_4. $ равны между собой. Для начала упростим задачу и докажем следующее: $B_1 B_2 = B_2 B_3$.

На рисунке прямые $a$ и $b$ параллельны. Следовательно, $A_1 B_1 B_2 A_2$ и $A_2 B_2 B_3 A_3$ — параллелограммы. Это означает, что противоположные стороны параллелограммов равны, следовательно, $A_1 A_2 = B_1 B_2, A_2 A_3 = B_2 B_3$. И из $A_1 A_2=A_2 A_3$ следует, что $B_1 B_2= B_2 B_3$.

Есть и другой случай, когда прямые $a$ и $b$ не параллельны:

Рисунок 4. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Проведём такую прямую $c$, которая параллельна $a$:

Рисунок 5. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Прямая $c$ пересекает $A_2 B_2$ и $A_3 B_3$ соответственно в т. $C_1, C_2$. Так как $A_1 A_2=A_2 A_3$, то, по аналогии в предыдущем случае, $B_1 C_1 = C_1 C_2$.

Рассмотрим $\triangle C_2 B_1 B_3$. $C_1$ — середина $B_1 C_2$. $B_2 C_1$ параллельна $B_3 C_2$.

Проведём через точку $B_3$ такую прямую, которая параллельна $B_1 C_2$.

Рисунок 6. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Точкой $D$ обозначено пересечение $B_2 C_1$ с проведённой прямой. Получаем параллелограмм $C_1 C_2 B_3 D$. Так как $C_1$ — середина $B_1 C_2$, а $C_1 C_2= B_3 D$ (как противоположные стороны параллелограмма), следовательно, $C_1 B_1 = B_3 D$.

Рассмотрим $\triangle C_1 B_1 B_2$ и $\triangle B_2 B_3 D$ Они равны согласно второму признаку равенства треугольников. То есть так как выполняются равенства $C_1 B_1 = B_3 D$, $\angle C_1 B_1 B_2 = \angle B_2 B_3 D$ и $\angle B_1 C_1 B_2=\angle B_2 D B_3$ (как лежащие накрест углы при пересечении параллельных прямых $B_1 C_2$ и $B_3 D$ секущими $B_1 B_3$ и $C_1 D$).

Следовательно, $B_1 B_2= B_2 B_3$.

Аналогично доказывается равенство $B_2 B_3=B_3 B_4$ и другие.

Таким образом, в данной статье мы полностью разобрали теорему Фалеса, произвели подробное её доказательство, фигурируя известными понятиями.

Источник

Теорема Фалеса. Доказательство

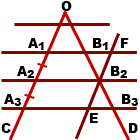
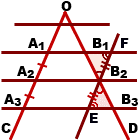
Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Дано : ∠COD,

A1B1 ∥ A2B2 ∥ A3B3,

A1, A2, A3 ∈OC, B1, B2, B3 ∈OD,

1) Через точку B2 проведем прямую EF, EF ∥ A1A3.

2) Рассмотрим четырехугольник A1FB2A2.

— A1F ∥ A2B2 (по условию),

— A1A2 ∥ FB2 (по построению).

Следовательно, A1FB2A2 — параллелограмм (по определению).

По свойству противолежащих сторон параллелограмма, A1A2=FB2.

3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E.

4) Так как A1A2=A2A3 (по условию), то FB2=B2E.

5) Рассмотрим треугольники B2B1F и B2B3E.

— FB2=B2E (по доказанному),

— ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF).

Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3.

Что и требовалось доказать.

8 Comments

Там где вертикальные углы равны, угол второй не тот выбран.

Спасибо, Eldar! Подкорректировано.

Спаcибо огромное*-*
Вы спасли мне жизнь, я таки всё понял

Пожалуйста! Успехов Вам в усвоении новых знаний! Разобраться в геометрии не так уж и сложно. Главное — делать это систематически.

Источник

Теорема Фалеса

Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.

Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.

Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.

А можно и в такой:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.

Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А₁В₁ могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Для иллюстрации можно воспользоваться рисунком 1.

Как пользоваться теоремой Фалеса на практике

Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.

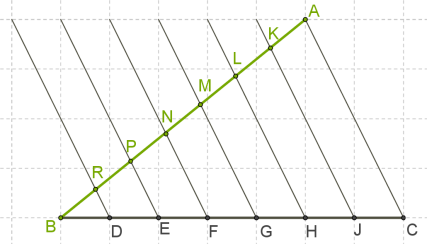
Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Обратная теорема Фалеса

Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:

Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.

Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.

Доказательство теоремы Фалеса

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

Выберем точку В₂ и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А₁А₃ || EF. Рассматривая четырехугольник

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

Кто впервые доказал теорему о пропорциональных отрезках

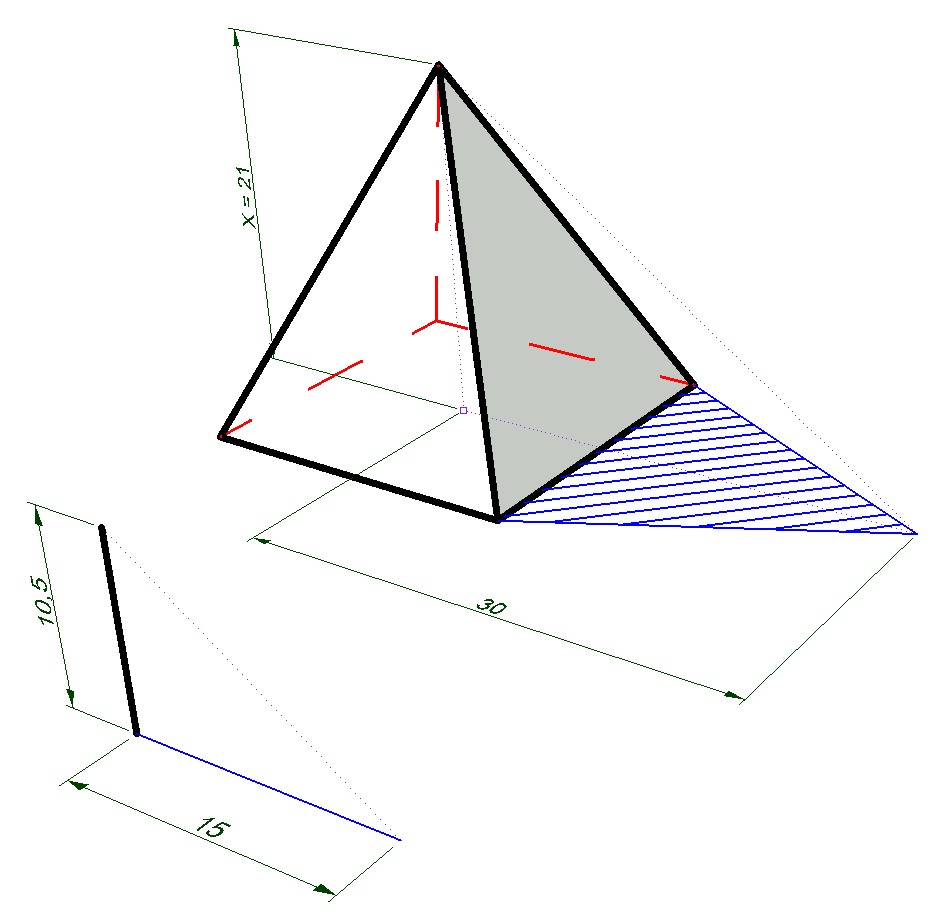
По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.

Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.

Источник