Факторный анализ. Дисперсионный анализ
Дисперсионный анализ
Дисперсионным анализом называют совокупность статистических методов, предназначенных для обработки данных экспериментов, целью которых являлось не установление каких-то свойств и параметров, а сравнение эффектов различных воздействий на каком-либо экспериментальном материале. Методы дисперсионного анализа используются для проверки гипотез о наличии связи между результативным признаком и исследуемыми факторами, а также для установления силы влияния факторов и их взаимодействий.
Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.
Проводится в среде MS Excel с помощью инструмента «Однофакторный дисперсионный анализ» Пакета анализа.
Результаты выполнения анализа:
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| x1 | 3200,2 | 160,01 | 3051,297 | |||
| x2 | 3178,8 | 158,94 | 3325,768 | |||
| x3 | 609622,5 | 30481,12 | 1,1E+08 | |||
| x4 | 40,6 | 2,03 | 14,87379 | |||
| x5 | 103692,6 | 5184,63 | 9979,812 | |||
| x6 | 59955,6 | |||||
| x7 | 49158,25 | 760820,5 | ||||
| x8 | 18569,75 | |||||
| x9 | 725,6142 | 36,28071 | 92,12897 | |||
| x10 | 107,462 | 5,3731 | 2,009487 | |||
| x11 | 97,1 | 12,62105 | ||||
| x12 | 21772,73 | 1088,637 | 29943,88 | |||
| x13 | 1265,171 | 63,25855 | 823,3025 | |||
| x14 | 1096,61 | 54,8305 | 778,4797 | |||
| x15 | 258,9353 | 12,94677 | 26,41525 | |||
| x16 | 46,2116 | 2,31058 | 0,490652 | |||
| x17 | 52055,2 | 2602,76 | 5833,25 | |||
| x18 | 5316,821 | 265,841 | 5571,812 | |||
| x19 | 197,8261 | 9,891305 | 11,80556 | |||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 1,17E+11 | 6,48E+09 | 822,8476 | 2,5054E-280 | 1,632496479 | |
| Внутри групп | 2,84E+09 | |||||
| Итого | 1,2E+11 |
Внутригрупповая изменчивость (SS) обычно называется остаточной компонентой или дисперсией ошибки. Это значит, что обычно при проведении эксперимента она может быть предсказана или объяснена. С другой стороны, SS между группами можно объяснить различиями между средними значениями в группах. Иными словами, принадлежность к некоторой группе объясняет межгрупповую изменчивость, т.к. нам известно, что эти группы обладают разными средними значениями.
Проверка значимости в дисперсионном анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым разбросом и компоненты дисперсии, обусловленной внутригрупповым разбросом. Если верна нулевая гипотеза (равенство средних в двух выборках), то можно ожидать сравнительно небольшое различие выборочных средних из-за чисто случайной изменчивости. Поэтому, при нулевой гипотезе, внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли отношение дисперсией значимо больше 1. В нашем случае, критерий показывает, что различие между средними статистически значимо.
Методами факторного анализа решаются три основных вида задач:
· отыскание скрытых, но предполагаемых закономерностей, которые определяются воздействием внутренних или внешних причин (факторов) на изучаемый процесс;
· выявление и изучение статистической связи признаков с факторами или главными компонентами;
· сжатие информации путем описания процесса при помощи общих факторов или главных компонент, число которых меньше количества первоначально взятых признаков (параметров), однако с той или иной степенью точности обеспечивающих воспроизводимость корреляционной матрицы.
Следует пояснить, что в факторном анализе понимается под сжатием информации. Дело в том, что корреляционная матрица получается путем обработки исходного массива данных. Корреляционная матрица образована из попарных коэффициентов корреляции компонент случайного вектора. Предполагается, что та же самая корреляционная матрица может быть получена с использованием тех же объектов, но описанных меньшим числом параметров. Таким образом, якобы происходит уменьшение размерности задачи, хотя на самом деле это не так. Это не сжатие информации в общепринятом смысле — восстановить исходные данные по корреляционной матрице нельзя.
Проведем факторный анализ для показателей, участвовавших в регрессионном анализе, с помощью программы AtteStat, которая является приложением для Excel. Были получены следующие результаты:
| Корреляционная матрица | |||||||||
| 1,000 | 0,896 | 0,928 | 0,898 | 0,966 | 0,986 | 0,993 | 0,936 | 0,886 | 0,997 |
| 0,896 | 1,000 | 0,828 | 0,925 | 0,916 | 0,902 | 0,898 | 0,771 | 0,871 | 0,899 |
| 0,928 | 0,828 | 1,000 | 0,877 | 0,884 | 0,917 | 0,919 | 0,859 | 0,948 | 0,918 |
| 0,898 | 0,925 | 0,877 | 1,000 | 0,950 | 0,919 | 0,864 | 0,714 | 0,945 | 0,887 |
| 0,966 | 0,916 | 0,884 | 0,950 | 1,000 | 0,988 | 0,940 | 0,831 | 0,887 | 0,954 |
| 0,986 | 0,902 | 0,917 | 0,919 | 0,988 | 1,000 | 0,972 | 0,897 | 0,886 | 0,977 |
| 0,993 | 0,898 | 0,919 | 0,864 | 0,940 | 0,972 | 1,000 | 0,960 | 0,862 | 0,996 |
| 0,936 | 0,771 | 0,859 | 0,714 | 0,831 | 0,897 | 0,960 | 1,000 | 0,738 | 0,945 |
| 0,886 | 0,871 | 0,948 | 0,945 | 0,887 | 0,886 | 0,862 | 0,738 | 1,000 | 0,876 |
| 0,997 | 0,899 | 0,918 | 0,887 | 0,954 | 0,977 | 0,996 | 0,945 | 0,876 | 1,000 |
| Метод главных факторов | |||||||||
| Число положительных собственных значений | |||||||||
| Число факторов | |||||||||
| Матрица факторного отображения | |||||||||
| 0,991 | -0,108 | -0,021 | -0,044 | -0,026 | -0,026 | -0,030 | 0,023 | -0,020 | -0,006 |
| 0,930 | 0,177 | -0,220 | 0,228 | 0,050 | -0,003 | 0,002 | 0,005 | 0,001 | -0,002 |
| 0,948 | 0,022 | 0,300 | 0,018 | 0,090 | 0,030 | -0,034 | 0,001 | 0,003 | 0,000 |
| 0,938 | 0,322 | -0,052 | -0,055 | -0,063 | 0,081 | -0,006 | -0,005 | -0,004 | 0,000 |
| 0,974 | 0,078 | -0,138 | -0,157 | 0,039 | -0,018 | 0,002 | 0,015 | 0,011 | 0,011 |
| 0,987 | -0,036 | -0,064 | -0,120 | 0,059 | -0,010 | 0,043 | -0,018 | -0,005 | -0,010 |
| 0,983 | -0,173 | -0,028 | 0,041 | -0,013 | -0,020 | -0,021 | -0,026 | -0,012 | 0,011 |
| 0,904 | -0,415 | 0,040 | 0,062 | -0,025 | 0,046 | 0,046 | 0,011 | 0,004 | 0,002 |
| 0,929 | 0,276 | 0,227 | 0,046 | -0,053 | -0,054 | 0,040 | 0,002 | 0,001 | 0,002 |
| 0,988 | -0,133 | -0,034 | -0,002 | -0,060 | -0,021 | -0,036 | -0,008 | 0,022 | -0,007 |
| Выделенные и накопленные дисперсии (в %) | |||||||||
| 91,70 | 91,70 | ||||||||
| 4,51 | 96,21 | ||||||||
| 2,20 | 98,41 | ||||||||
| 1,04 | 99,45 | ||||||||
| 0,27 | 99,72 | ||||||||
| 0,14 | 99,87 | ||||||||
| 0,09 | 99,96 | ||||||||
| 0,02 | 99,98 | ||||||||
| 0,01 | 100,00 | ||||||||
| 0,00 | 100,00 | ||||||||
| Повернутая матрица факторного отображения | |||||||||
| 0,713 | 0,442 | 0,451 | -0,297 | -0,002 | -0,007 | -0,045 | 0,014 | -0,0000001 | 0,0000004 |
| 0,466 | 0,774 | 0,407 | -0,130 | 0,033 | 0,021 | -0,005 | -0,024 | -0,0000004 | 0,0000004 |
| 0,594 | 0,304 | 0,715 | -0,165 | 0,024 | 0,122 | 0,004 | -0,023 | -0,0000002 | 0,0000001 |
| 0,353 | 0,617 | 0,599 | -0,347 | -0,126 | -0,019 | -0,004 | 0,017 | 0,0000001 | -0,0000001 |
| 0,545 | 0,545 | 0,443 | -0,458 | 0,021 | 0,011 | -0,007 | 0,037 | 0,0000000 | 0,0000008 |
| 0,646 | 0,472 | 0,450 | -0,389 | 0,012 | 0,013 | 0,004 | -0,146 | 0,0000000 | 0,0000001 |
| 0,762 | 0,449 | 0,412 | -0,210 | 0,004 | 0,003 | -0,046 | -0,028 | 0,0000000 | 0,0000036 |
| 0,903 | 0,273 | 0,307 | -0,120 | -0,015 | 0,001 | 0,038 | 0,000 | -0,0000011 | -0,0000001 |
| 0,394 | 0,452 | 0,777 | -0,179 | 0,009 | -0,071 | -0,019 | -0,008 | -0,0000011 | 0,0000008 |
| 0,733 | 0,454 | 0,429 | -0,255 | -0,020 | -0,024 | -0,077 | 0,027 | 0,0000000 | -0,0000004 |

Анализируя полученные результаты, приходим к выводу, что на ВНП самое сильное и значимое влияние оказывает только один фактор (дисперсия 91,70%).
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Факторный и дисперсионный анализ в Excel с автоматизацией подсчетов
Чтобы проанализировать изменчивость признака под воздействием контролируемых переменных, применяется дисперсионный метод.
Для изучения связи между значениями – факторный метод. Рассмотрим подробнее аналитические инструменты: факторный, дисперсионный и двухфакторный дисперсионный метод оценки изменчивости.
Дисперсионный анализ в Excel
Условно цель дисперсионного метода можно сформулировать так: вычленить из общей вариативности параметра 3 частные вариативности:
- 1 – определенную действием каждого из изучаемых значений;
- 2 – продиктованную взаимосвязью между исследуемыми значениями;
- 3 – случайную, продиктованную всеми неучтенными обстоятельствами.
В программе Microsoft Excel дисперсионный анализ можно выполнить с помощью инструмента «Анализ данных» (вкладка «Данные» — «Анализ»). Это надстройка табличного процессора. Если надстройка недоступна, нужно открыть «Параметры Excel» и включить настройку для анализа.
Работа начинается с оформления таблицы. Правила:
- В каждом столбце должны быть значения одного исследуемого фактора.
- Столбцы расположить по возрастанию/убыванию величины исследуемого параметра.
Рассмотрим дисперсионный анализ в Excel на примере.
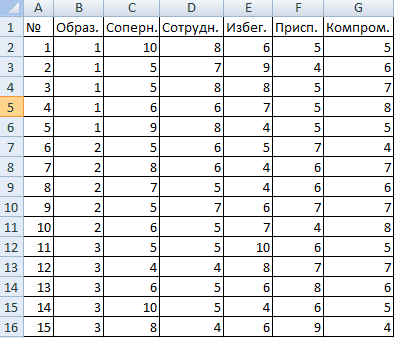
Психолог фирмы проанализировал с помощью специальной методики стратегии поведения сотрудников в конфликтной ситуации. Предполагается, что на поведение влияет уровень образования (1 – среднее, 2 – среднее специальное, 3 – высшее).
Внесем данные в таблицу Excel:
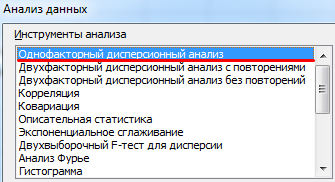
- Открываем диалоговое окно нашего аналитического инструмента. В раскрывшемся списке выбираем «Однофакторный дисперсионный анализ» и нажимаем ОК.
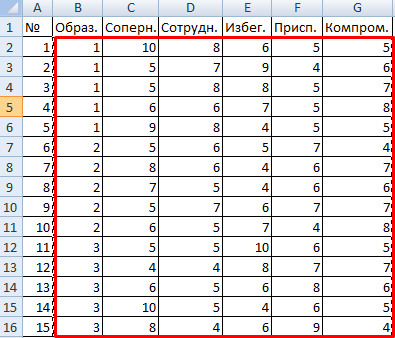
- В поле «Входной интервал» ввести ссылку на диапазон ячеек, содержащихся во всех столбцах таблицы.
- «Группирование» назначить по столбцам.
- «Параметры вывода» — новый рабочий лист. Если нужно указать выходной диапазон на имеющемся листе, то переключатель ставим в положение «Выходной интервал» и ссылаемся на левую верхнюю ячейку диапазона для выводимых данных. Размеры определятся автоматически.
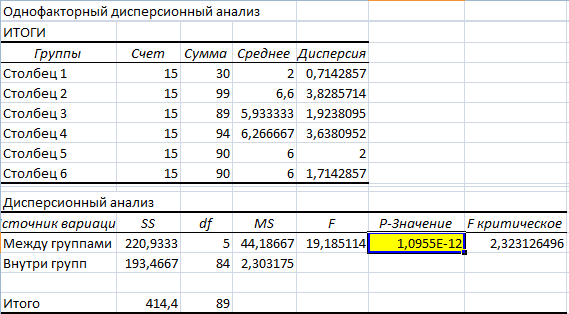
- Результаты анализа выводятся на отдельный лист (в нашем примере).
Значимый параметр залит желтым цветом. Так как Р-Значение между группами больше 1, критерий Фишера нельзя считать значимым. Следовательно, поведение в конфликтной ситуации не зависит от уровня образования.
Факторный анализ в Excel: пример
Факторным называют многомерный анализ взаимосвязей между значениями переменных. С помощью данного метода можно решить важнейшие задачи:
- всесторонне описать измеряемый объект (причем емко, компактно);
- выявить скрытые переменные значения, определяющие наличие линейных статистических корреляций;
- классифицировать переменные (определить взаимосвязи между ними);
- сократить число необходимых переменных.
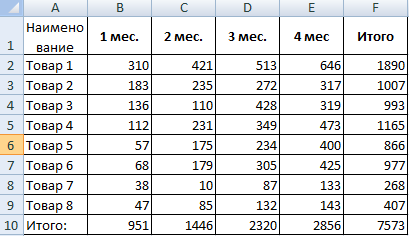
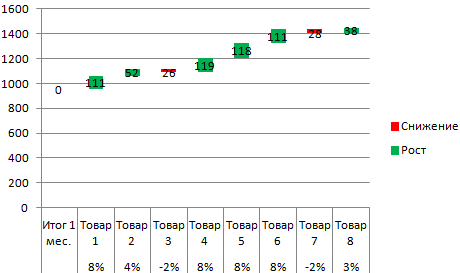
Рассмотрим на примере проведение факторного анализа. Допустим, нам известны продажи каких-либо товаров за последние 4 месяца. Необходимо проанализировать, какие наименования пользуются спросом, а какие нет.
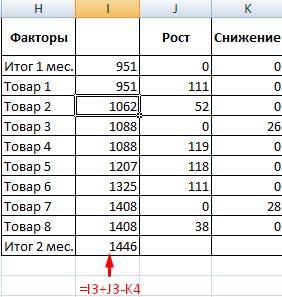
- Посмотрим, за счет, каких наименований произошел основной рост по итогам второго месяца. Если продажи какого-то товара выросли, положительная дельта – в столбец «Рост». Отрицательная – «Снижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница между 2 и 1 месяцем. Формула для «снижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во втором столбце – сумма предыдущего значения и предыдущего роста за вычетом текущего снижения.
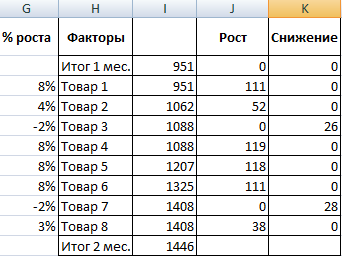
- Рассчитаем процент роста по каждому наименованию товара. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «снижения» к итогу за 2 месяц.
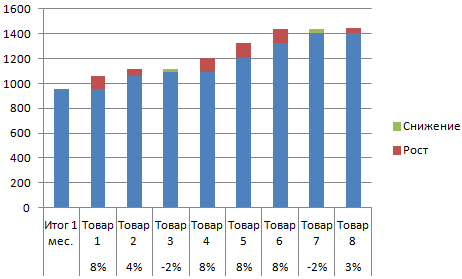
- Выделяем область данных для построения диаграммы. Переходим на вкладку «Вставка» — «Гистограмма».
- Поработаем с подписями и цветами. Уберем накопительный итог через «Формат ряда данных» — «Заливка» («Нет заливки»). С помощью данного инструментария меняем цвет для «снижения» и «роста».
Теперь наглядно видно, продажи какого товара дают основной рост.
Двухфакторный дисперсионный анализ в Excel
Показывает, как влияет два фактора на изменение значения случайной величины. Рассмотрим двухфакторный дисперсионный анализ в Excel на примере.
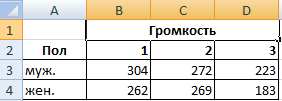
Задача. Группе мужчин и женщин предъявляли звук разной громкости: 1 – 10 дБ, 2 – 30 дБ, 3 – 50 дБ. Время ответа фиксировали в миллисекундах. Необходимо определить, влияет ли пол на реакцию; влияет ли громкость на реакцию.
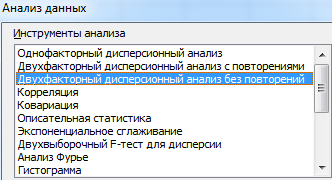
- Переходим на вкладку «Данные» — «Анализ данных» Выбираем из списка «Двухфакторный дисперсионный анализ без повторений».
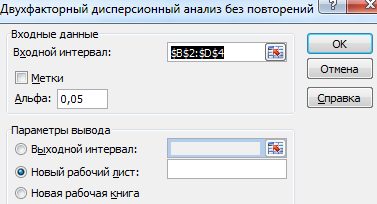
- Заполняем поля. В диапазон должны войти только числовые значения.
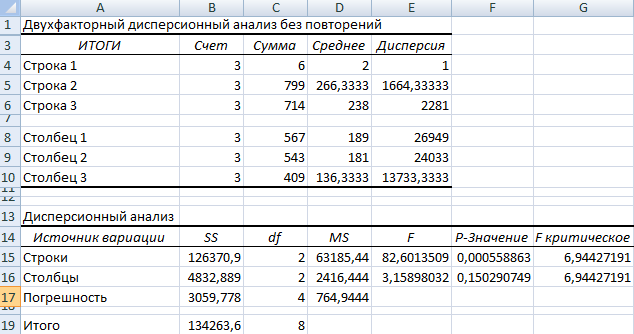
- Результат анализа выводится на новый лист (как было задано).
Та как F-статистики (столбец «F») для фактора «Пол» больше критического уровня F-распределения (столбец «F-критическое»), данный фактор имеет влияние на анализируемый параметр (время реакции на звук).
Источник